广东省东莞市横沥镇2023年中考数学一模试卷

试卷更新日期：2024-03-05 类型：中考模拟

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 中国古代著作《九章算术》在世界数学史上首次正式引入负数．如果盈利90元记作+90元，那么亏本60元记作（）

A、﹣60元 B、﹣70元 C、+60元 D、+70元

查看试题解析
2. 卢塞尔体育场是卡塔尔世界杯的主体育场，由中国建造，是卡塔尔规模最大的体育场.世界杯之后，将有约170000个座位将捐赠给需要体育基础设施的国家，其中大部分来自世界杯决赛场地卢塞尔体育场，170000这个数用科学记数法表示为（）

A、 $0.17 \times 1 0^{5}$ B、 $1.7 \times 1 0^{5}$ C、 $17 \times 1 0^{4}$ D、 $1.7 \times 1 0^{6}$

查看试题解析
3. 下列图形中，既是轴对称又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 一组数据：7，5，9，3，9，15，关于这组数据说法错误的是（）

A、极差是12 B、众数是9 C、中位数是7 D、平均数是8

查看试题解析
5. （﹣ $\frac{1}{2}$ ）²⁰¹⁹•（﹣2）²⁰²⁰的计算结果是（）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析
6. 不等式3x＞﹣6的解集是（）

A、x＞ $\frac{1}{2}$ B、x＞2 C、x＞﹣ $\frac{1}{2}$ D、x＞﹣2

查看试题解析
7. 有一个正方体骰子，6个面分别标有1～6这6个整数，投掷这个正方体骰子一次，朝上一画出现奇数的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{6}$ D、 $\frac{1}{4}$

查看试题解析
8. 如图，AB为⊙O的直径，CD是⊙O的弦，若∠ACD＝33°，则∠BAD的度数为（）

A、33° B、47° C、57° D、66°

查看试题解析
9. 锐角△ABC中，BC＝6，S_△_ABC＝12，两动点M ， N分别在边AB ， AC上滑动，且MN∥BC ， MP⊥BC ， NQ⊥BC得矩形MPQN ，设MN的长为x ，矩形MPQN的面积为y ，则y关于x的函数图象大致形状是（）

A、 B、 C、 D、

查看试题解析
10. 如图，正方形ABCD的边长是2，其面积标记为S₁ ，以CD为斜边作等腰直角三角形CDE ，以该等腰直角三角形的一条直角边DE为边向外作正方形，其面积标记为S₂按照此规律继续作图，则S₂₀₂₁的值为（）

A、 $\frac{1}{2^{2018}}$ B、 $\frac{1}{2^{2019}}$ C、 $\frac{1}{2^{2020}}$ D、 $\frac{1}{2^{2021}}$

查看试题解析

二、填空题（共7小题，满分28分，每小题4分）

11. 点A（﹣1，4）与点B关于原点对称，则B的坐标为．

查看试题解析
12. 已知正n边形的每个内角为144°，则n＝.

查看试题解析
13. 若5x^a^﹣2y³与﹣3x⁴y^b是同类项，则a+b的值为．

查看试题解析
14. 若 $x^{2} + 3 x = 1$ ，则 $2021 + 2 x^{2} + 6 x$ 的值为．

查看试题解析
15. 如图，在矩形ABCD中， $A B = 2 \sqrt{3}$ ， BC＝6，点E在BC上，且CE＝AE，将 $△ A B C$ 沿对角线AC翻折到 $△ A F C$ ，连接EF．则 $\sin ∠ C E F =$ ．

查看试题解析
16. 如图，点A在反比例函数y＝ $\frac{2}{x}$ （x＞0）的图象上，过点A作AB⊥x轴，垂足为点B ，点C在y轴上，则△ABC的面积为．

查看试题解析
17. 如图， $E$ ， $F$ 分别是正方形 $A B C D$ 的边 $C B$ ， $A D$ 上的点，且 $C E = D F$ ， $A E$ 与 $B F$ 相交于 $O .$ 下列结论： $① A E = B F$ 且 $A E ⊥ B F$ ； $② S_{△ A O B} = S_{四边形 D E O F}$ ； $③ A D = O E$ ； $④$ 连接 $O C$ ，当 $E$ 为边 $D C$ 的中点时， $t a n ∠ E O C$ 值为 $\frac{1}{2}$ ，其中正确的结论有．

查看试题解析

三、解答题（共8小题，满分62分）

18. 计算：﹣|﹣3|+4cos45°﹣（﹣1）²⁰²³﹣ $\sqrt{8}$ ．

查看试题解析
19. 先化简：（ $\frac{a + 7}{a - 1} - \frac{2}{a + 1}$ ）÷ $\frac{a^{2} + 3 a}{a^{2} - 1}$ ，再从﹣3、﹣2、﹣1、0、1中选一个合适的数作为a的值代入求值.

查看试题解析
20. 如图，在△ABC中，∠B＝2∠C ，分别以点A ， C为圆心，大于 $\frac{1}{2} A C$ 的长为半径画弧，两弧在AC两侧分别交于P ， Q两点，作直线PQ交BC边于点D ，交AC于点E ， AB＝5，BC＝13，求BD的长．

查看试题解析
21. 为推广阳光体育“大课间”活动，我县某中学决定在学生中开设A：实心球．B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：

(1)、在这项调查中，共调查了多少名学生？

(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；

(3)、若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．

查看试题解析
22. 如图，在平面直角坐标系中，一次函数y＝kx+b与反比例函数y＝﹣ $\frac{6}{x}$ 的图象交于A（﹣1，m），B（n ， ﹣3）两点，一次函数y＝kx+b的图象与y轴交于点C ．

(1)、求一次函数的解析式；

(2)、根据函数的图象，直接写出不等式kx+b≤﹣ $\frac{6}{x}$ 的解集；

(3)、点P是x轴上一点，且△BOP的面积等于△AOB面积的2倍，求点P的坐标．

查看试题解析
23. 某中学开学初在商场购进A、B两种品牌的足球，购买A品牌足球花费了2500元，购买B品牌足球花费了2000元，且购买A品牌足球数量是购买B品牌足球数量的2倍，已知购买一个B品牌足球比购买一个A品牌足球多花30元．

(1)、求购买一个A品牌、一个B品牌的足球各需多少元；

(2)、该中学决定再次购进A、B两种品牌足球共50个，恰逢商场对两种品牌足球的售价进行调整，A品牌足球售价比第一次购买时提高了8%，B品牌足球按第一次购买时售价的9折出售，如果这所中学此次购买A、B两种品牌足球的总费用不超过3060元，那么该中学此次最多可购买多少个B品牌足球？

查看试题解析
24. 如图，AB是⊙O的直径，弦CD⊥AB于E ，与弦AF交于G ，过点F的直线分别与AB ， CD的延长线交于M ， N ， FN＝GN ．

(1)、求证：MN是⊙O的切线；

(2)、若BM＝1， $s i n M = \frac{4}{5}$ ，求AF的长．

查看试题解析
25. 如图，在平面直角坐标系中，二次函数y＝﹣x²＋bx＋c的图象与坐标轴交于A，B，C三点，其中点B的坐标为（1，0），点C的坐标为（0，4），点D的坐标为（0，2），点P为二次函数图象上的动点.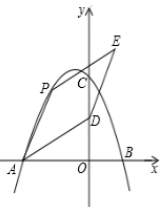

(1)、求二次函数的解析式和直线AD的解析式；

(2)、当点P位于第二象限内二次函数的图象上时，连接AD，AP，以AD，AP为邻边作平行四边形APED，设平行四边形APED的面积为S，求S的最大值.

查看试题解析