广东省广州市海珠区2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分）

1. 若气温为零上 $10 ° C$ 记作 $+ 10 ° C$ ，则 $- 3 ° C$ 表示气温为（）

A、零上 $3 ° C$ B、零下 $3 ° C$ C、零上 $7 ° C$ D、零下 $7 ° C$

查看试题解析
2. 将“784000”用科学记数法表示为（）

A、 $7.84 \times 1 0^{5}$ B、 $7.84 \times 1 0^{6}$ C、 $7.84 \times 1 0^{7}$ D、 $78.4 \times 1 0^{6}$

查看试题解析
3. 如图的平面图形绕直线l旋转一周，可以得到的立体图形是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $a^{2} b - a b^{2} = 0$ C、 $2 a b - 2 b a = 0$ D、 $a^{3} + a^{2} = a^{5}$

查看试题解析
5. 下列变形正确的是（）

A、若 $x + 5 = 1$ ，则 $x = 1 + 5$ B、若 $2 x = 8$ ，则 $x = 8 - 2$ C、若 $6 x = 3$ ，则 $x = \frac{6}{3}$ D、若 $\frac{2}{3} x = 5$ ，则 $x = 5 \div (\frac{2}{3})$

查看试题解析
6. 若关于x的方程2x+a＝9﹣a（x﹣1）的解是x＝3，则a的值为（）

A、1 B、2 C、﹣3 D、5

查看试题解析
7. 如图一个正方形的平面展开图如图所示，将它折成正方体后，“保”字对面的字是（）．

A、碳 B、低 C、绿 D、色

查看试题解析
8. 在纸上画了一条数轴后，折叠纸面，使数轴上表示 $- 1$ 的点与表示3的点重合，表示数7的点与点A重合，则点A表示的数是（）

A、5 B、 $- 3$ C、 $- 7$ D、 $- 5$

查看试题解析
9. 有一个魔术，魔术师背对小聪，让小聪拿着扑克牌按下列四个步骤操作：
①第一步：分发左、中、右三堆牌，每堆牌不少于五张，且各堆牌的张数相同；

②第二步：从左边一堆拿出五张，放入中间一堆；

③第三步：从右边一堆拿出三张，放入中间一堆；

④第四步：右边一堆有几张牌，就从中间一堆拿几张牌放入右边一堆。

这时，魔术师准确说出了中间一堆牌现有的张数，则他说出的张数是（）

A、8 B、9 C、10 D、11

查看试题解析
10. $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} (a b c \neq 0)$ 的所有可能的值有（）个

A、2 B、3 C、4 D、5

查看试题解析

二、填空题（本题共6小题，每小题3分，共18分）

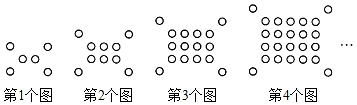
11. - 2023 的相反数是.

查看试题解析
12. 若 $∠ α = 32 °$ ，则 $∠ α$ 的余角的度数为．

查看试题解析
13. “某数与6的和的一半等于12”，设某数为x ，则可列方程．

查看试题解析
14. 若单项式 $- 2 a x^{2} y^{n + 1}$ 与 $- 3 a x^{m} y^{4}$ 的差是 $a x^{2} y^{4}$ ，则 $2 m + 3 n =$ ．

查看试题解析
15. 已知线段 $A C$ 和线段 $B C$ 在同一直线上，如果 $A C = 6 c m$ ， $B C = 4 c m$ ，则线段 $A C$ 和线段 $B C$ 的中点之间的距离为 $c m$ ．

查看试题解析
16. 如图所示的图形都由同样大小的小圆圈按一定规律所组成的，若按此规律排列下去，则第n个图形中有个小圆圈．

查看试题解析

三、解答题（本题共9小题，共72分．解答要求写出文字说明，证明过程或计算步骤）

17. 计算： ${(- 3)}^{2} \times 2 - | - 36 | \div 4$

查看试题解析
18. 解方程：

(1)、 $4 x - 1 = 2 x + 5$ ．

(2)、 $\frac{x - 3}{2} + \frac{x - 1}{3} = 4$ ．

查看试题解析
19. 已知多项式 $A = 3 (2 a^{2} - 2 a b + b^{2}) - 2 (a^{2} - 3 a b - \frac{5}{2} b^{2})$ ．

(1)、化简A；

(2)、若 $a^{2} + 2 b^{2} = 5$ ，求多项式A的值．

查看试题解析
20. 如图，已知平面内的四个点A ， B ， C ， D ，请用直尺和圆规完成下列作图．（不写画法，保留画图痕迹）

(1)、画直线AB；

(2)、画射线AC；

(3)、连接BC并延长BC到E ，使得 $C E = A B + B C$ ；

(4)、在线段BD上取点P ，使 $P A + P C$ 的值最小，并说明理由．

查看试题解析
21. 如图，线段AB＝20，BC＝15，点M是AC的中点．

(1)、求线段AM的长度；

(2)、在CB上取一点N，使得CN：NB＝2：3．求MN的长．

查看试题解析
22. 某超市为了吸引顾客，推出两种不同的优惠销售方式，方式一：累计购买商品总价超过200元，超出的部分按原价8折优惠；方式二：累计购买商品总价超过100元，超出部分按原价8.5折优惠．

(1)、甲顾客准备购买300元的商品，你认为他应该选择哪种优惠方式？请说明理由．

(2)、设乙顾客计划累计购物x元 $(x > 200)$ ，他选择何种优惠方式更省钱？

查看试题解析
23. 定义：关于x的方程 $a x - b = 0$ 与方程 $b x - a = 0$ （a ， b均为不等于0的常数）称互为“反对方程”，例如：方程 $2 x - 1 = 0$ 与方程 $x - 2 = 0$ 互为“反对方程”．

(1)、若关于x的方程 $2 x - 3 = 0$ 与方程 $3 x - c = 0$ 互为“反对方程”，则 $c =$ ．

(2)、若关于x的方程 $2 x - 3 = d$ 与其“反对方程”的解都是整数，求整数d的值．

(3)、已知关于x的一元一次方程 $\frac{2022}{2023} x + 5 = 7 x + m$ 的解为 $x = - \frac{1}{2}$ ，那么关于y的一元一次方程 $(m - 5) (y + 2) + 7 = \frac{2022}{2023}$ 的解为．（请直接写出答案）

查看试题解析
24. 请阅读下列材料，并解答相应的问题：
“九宫图”源于我国古代夏禹时期的“洛书”（如图1），是世界上最早的矩阵，又称幻方．用今天的数学符号表示，洛书就是一个三阶幻方（如图2），“幻方”需要满足的条件是每一行、每一列和每条对角线上各个数之和都相等．

(1)、设图3三阶幻方中间的数字是x ，用x的代数式表示幻方中9个数的和为；每一行三个数的和为；

(2)、图4是一个三阶幻方，那么标有x的方格中所填的数是多少？请写出解题过程．

(3)、由三阶幻方可以衍生出许多有特定规律的新幻方，在如图5所示的“幻方”中，每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等， $x = k + 1$ ， $y = k - 1$ ，求 $a - b - c + d$ 的值．

查看试题解析
25. 如图1，点O为直线 $A B$ 上一点，过点O作射线 $O C$ ，使 $∠ B O C = 110 °$ ，将一直角三角板的直角顶点放在点O处（ $∠ O M N = 30 °$ ），一边 $O M$ 在射线 $O B$ 上，另一边 $O N$ 在直线 $A B$ 的下方．

(1)、将图1中的三角板绕点O逆时针旋转至图2，使一边 $O M$ 在 $∠ B O C$ 的内部，且恰好平分 $∠ B O C$ ．求 $∠ B O N$ 的度数．

(2)、将图1中三角板绕点O以每秒 $5 °$ 的速度沿逆时针方向旋转一周，同时射线 $O P$ 从 $O C$ 开始绕点O以每秒 $2 °$ 的速度沿顺时针方向旋转，当三角板停止运动时，射线 $O P$ 也停止运动．设旋转时间为t秒．
①在运动过程中，当 $∠ P O M = 40 °$ 时，求t的值；
②当 $40 < t < 54$ 时，在旋转的过程中 $∠ C O N$ 与 $∠ A O M$ 始终满足关系 $m ∠ C O N + ∠ A O M = n °$ （m ， n为常数），求 $m + n$ 的值．

查看试题解析