广东省深圳市盐田区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 下列实数中是无理数的是（）

A、 $0.3$ B、 $- 2023$ C、 $\sqrt{3}$ D、 $\frac{3}{2}$

查看试题解析
2. 如图，直线 $a$ ， $b$ 被第三条直线 $c$ 所截．由“ $∠ 1 = ∠ 2$ ”，得到“ $a ∥ b$ ”的依据是（）

A、两直线平行，同位角相等 B、同位角相等，两直线平行 C、两直线平行，内错角相等 D、内错角相等，两直线平行

查看试题解析
3. 秦兵马俑的发现被誉为“世界第八大奇迹”，兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 $\frac{\sqrt{5} - 1}{2}$ ，请你估算 $\sqrt{5} - 1$ 的值（）

A、在0和1之间 B、在1和2之间 C、在2和3之间 D、在3和4之间

查看试题解析
4. 某校九年级体育模拟测试中，六名男生引体向上的成绩如下 $（$ 单位：个 $）$ ：10、6、9、11、8、10，下列关于这组数据描述正确的是（）

A、极差是6 B、中位数是11 C、平均数是 $9.5$ D、方差是 $\frac{8}{3}$

查看试题解析
5. 在 $△ A B C$ 中，若一个内角等于另外两个角的差，则（）

A、必有一个角等于 $30 °$ B、必有一个角等于 $45 °$ C、必有一个角等于 $60 °$ D、必有一个角等于 $90 °$

查看试题解析
6. 若点 $P (m + 5 ， m - 3)$ 在x轴上，则点P的坐标为（）

A、 $(8 ， 0)$ B、 $(0 ， - 8)$ C、 $(4 ， 0)$ D、 $(0 ， - 4)$

查看试题解析
7. 一次函数 $y = - 2 x + 4$ 的图象是由 $y = - 2 x$ 的图象平移得到的，则移动方法为（）

A、向右平移 $4$ 个单位 B、向左平移 $4$ 个单位 C、向上平移 $4$ 个单位 D、向下平移 $4$ 个单位

查看试题解析
8. 以二元一次方程 $2 x + y = - 1$ 的解为坐标的点组成的图象画在坐标系中可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，若知道图中阴影部分的面积，则一定能求出（）

A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析
10. 如图，在平面直角坐标系中，直线 $y = x + 2$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，点 $P$ 是线段 $A B$ 的中点，点 $C$ 是 $x$ 轴上的一个动点，连接 $B C$ ，以 $B C$ 为直角边，点 $B$ 为直角顶点作等腰直角 $△ B C D$ ，连接 $D P$ ．则 $D P$ 长度的最小值是（）

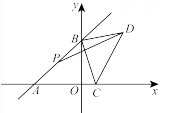A、1 B、2 C、 $2 \sqrt{2}$ D、3

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分．

11. $\sqrt{81}$ 的平方根是．

查看试题解析
12. 命题“若 $a \neq b$ ， $b \neq c$ ，则 $a \neq c$ ”是命题．（填“真”“假”）

查看试题解析
13. 已知一次函数 $y = m x^{| m |} + 1$ ，它的图象经过第一、二、四象限，则 $m =$ ．

查看试题解析
14. 如图，已知A地在B地正南方3千米处，甲、乙两人同时分别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行时间t（小时）之间的函数关系图象如图所示的AC和BD给出，当他们行走3小时后，他们之间的距离为千米．

查看试题解析
15. 如图，在长方形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点E为 $A B$ 上一点，将 $△ B C E$ 沿 $C E$ 翻折至 $△ F C E$ ，延长 $C F$ 交 $A B$ 于点O ，交 $D A$ 的延长线于点G ，且 $E F = A G$ ，则 $B E$ 的长为．

查看试题解析

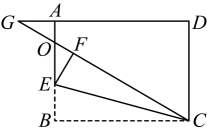
三、解答题：本题共7小题，共55分，解答应写出文字说明、证明过程或演算步骤．

16. 计算：

(1)、 $\sqrt{32} - \sqrt{8} - 4 \sqrt{\frac{1}{2}}$ ；

(2)、 $| 1 - \sqrt{2} | + \sqrt[3]{- 1}$ ．

查看试题解析

17. 下面是小乐同学解二元一次方程组的过程，请认真阅读并完成相应的任务．

解方程组： ${\begin{array}{l} 3 x - y = 8 ， ① \\ 9 x - 4 y = 20 ． ② \end{array}$

解：① $\times 3$ ，得 $9 x - 3 y = 24$ ． ③……第一步

③ $-$ ②，得 $- y = 4$ ． ……第二步

$y = - 4$ ． ……第三步

将 $y = - 4$ 代入①，得 $x = \frac{4}{3}$ ． ……第四步

所以，原方程组的解为 ${\begin{array}{l} x = \frac{4}{3} ， \\ y = - 4 \end{array}$ ……第五步

填空：

(1)、这种求解二元一次方程组的方法叫做法；以上求解步骤中，第一步的依据是．

(2)、第步开始出现错误．

(3)、直接写出该方程组的正确解：．

查看试题解析

18. 在平面直角坐标系中， $△ A B C$ 的位置如图所示，已知点 $A$ 的坐标是 $(- 4 ， 3)$

(1)、点 $B$ 的坐标为（，），点 $C$ 的坐标为（，）

(2)、求 $△ A B C$ 的面积．

(3)、作点 $C$ 关于 $y$ 轴的对称点 $C^{'}$ ，那么 $A 、 C^{'}$ 两点之间的距离是．

查看试题解析
19. 【问题情境】
数学课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．
【实践发现】
同学们随机收集香樟树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位： $c m$ ），宽x（单位： $c m$ ）的数据后，分别计算长宽比，整理数据如下：

1
2
3
4
5
6
7
8
9
10
香樟树叶的长宽比
$2.5$
$2.2$
$2.6$
$2.3$
$2.4$
$\begin{array}{l} 2.4 \end{array}$
$\begin{array}{l} 2.4 \end{array}$
$\begin{array}{l} 2.4 \end{array}$
$\begin{array}{l} 2.3 \end{array}$
$\begin{array}{l} 2.2 \end{array}$
荔枝树叶的长宽比
$\begin{array}{l} 2.0 \end{array}$
$\begin{array}{l} 2.0 \end{array}$
$\begin{array}{l} 2.0 \end{array}$
$\begin{array}{l} 2.4 \end{array}$
$\begin{array}{l} 1.8 \end{array}$
$\begin{array}{l} 2.1 \end{array}$
$\begin{array}{l} 1.8 \end{array}$
$\begin{array}{l} 2.0 \end{array}$
$\begin{array}{l} 1.3 \end{array}$
$\begin{array}{l} 1.9 \end{array}$
【实践探究】
分析数据如下：

平均数
中位数
众数
方差
香樟树叶的长宽比
$\begin{array}{l} 2.37 \end{array}$
m
$\begin{array}{l} 2.4 \end{array}$
$\begin{array}{l} 0.0141 \end{array}$
荔枝树叶的长宽比
$\begin{array}{l} 1.93 \end{array}$
$\begin{array}{l} 2.0 \end{array}$
n
$\begin{array}{l} 0.0701 \end{array}$
【问题解决】

(1)、上述表格中： $m =$ ， $n =$ ．

(2)、通过数据，同学们总结出了一些结论：
① $A$ 同学说：“从树叶的长宽比的方差来看，香樟树叶的形状差别比荔枝树叶”．（填“小”或者“大”）
② $B$ 同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的倍．”

(3)、现有一片长 $11 c m$ ，宽 $5.6 c m$ 的树叶，请判断这片树叶更可能来自香樟、荔枝中的哪种树？并给出你的理由．

查看试题解析
20. 已知 $△ A C B$ 与 $△ E C D$ 都是等腰直角三角形， $∠ A C B = ∠ E C D = 90 °$ ， $△ A C B$ 的顶点A在 $△ E C D$ 的斜边 $D E$ 上．

(1)、如图1，若 $E D ∥ C B$ ， $A C = 1$ ，求 $E D$ 的长；

(2)、如图2，求证 $A E^{2} + A D^{2} = 2 A C^{2}$ ．

查看试题解析
21. 为了迎接今年9月末至10月初在杭州举行的第19届亚运会，某旅游商店购进若干明信片和吉祥物钥匙扣．这两种物品的进价、标价如下表所示．

进价
标价
明信片
5元/套
10元/套
吉祥物钥匙扣
18元/个
30元/个
为了促销，商店对吉祥物钥匙扣进行8折销售．

(1)、若张老师在本店同时购买吉祥物钥匙扣和明信片共46件，花费600元．请问店主获利多少元？

(2)、张老师在本店花费600元购买吉祥物钥匙扣和明信片若干件，两种都买且钱要用完．请帮助张老师策划所有可行的购买方案．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，正比例函数 $y = m x (m \neq 0)$ 的图象经过点 $A (2 ， 4)$ ，过点A的直线 $y = k x + b (0 < k < 2)$ 与x轴、y轴分别交于B ， C两点．

(1)、求正比例函数的表达式；

(2)、若 $△ A O B$ 的面积为 $△ B O C$ 的面积的 $\frac{4}{3}$ 倍，求直线 $y = k x + b$ 的表达式；

(3)、在（2）的条件下，在线段 $B C$ 上找一点D ，使 $O C$ 平分 $∠ A O D$ ，求点D的坐标．

查看试题解析

	1	2	3	4	5	6	7	8	9	10
香樟树叶的长宽比	$2.5$	$2.2$	$2.6$	$2.3$	$2.4$	$\begin{array}{l} 2.4 \end{array}$	$\begin{array}{l} 2.4 \end{array}$	$\begin{array}{l} 2.4 \end{array}$	$\begin{array}{l} 2.3 \end{array}$	$\begin{array}{l} 2.2 \end{array}$
荔枝树叶的长宽比	$\begin{array}{l} 2.0 \end{array}$	$\begin{array}{l} 2.0 \end{array}$	$\begin{array}{l} 2.0 \end{array}$	$\begin{array}{l} 2.4 \end{array}$	$\begin{array}{l} 1.8 \end{array}$	$\begin{array}{l} 2.1 \end{array}$	$\begin{array}{l} 1.8 \end{array}$	$\begin{array}{l} 2.0 \end{array}$	$\begin{array}{l} 1.3 \end{array}$	$\begin{array}{l} 1.9 \end{array}$

	平均数	中位数	众数	方差
香樟树叶的长宽比	$\begin{array}{l} 2.37 \end{array}$	m	$\begin{array}{l} 2.4 \end{array}$	$\begin{array}{l} 0.0141 \end{array}$
荔枝树叶的长宽比	$\begin{array}{l} 1.93 \end{array}$	$\begin{array}{l} 2.0 \end{array}$	n	$\begin{array}{l} 0.0701 \end{array}$

	进价	标价
明信片	5元/套	10元/套
吉祥物钥匙扣	18元/个	30元/个