广东省广州市番禺区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选择项中，只有一项是符合题目要求的．

1. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会，下列四个图分别是第24届冬奥会图标中的一部分，其中是轴对称图形的为（　　）

A、 B、 C、 D、

查看试题解析
2. 神舟十五号载人飞船与神舟十四号乘组在距离地球约400000米的中国空间站胜利会师，将400000用科学记数法表示为 $a \times 1 0^{n}$ ，下列说法正确的是（）

A、 $a = 400$ ， $n = 3$ B、 $a = 4$ ， $n = 5$ C、 $a = 4$ ， $n = 6$ D、 $a = 0.4$ ， $n = 6$

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ A = 50 °$ ， $∠ B = 70 °$ ，则外角 $∠ A C D$ 的度数是（）

A、 $110 °$ B、 $120 °$ C、 $130 °$ D、 $140 °$

查看试题解析
4. 下列运算正确的是（）

A、 $a^{2} \cdot a = a^{2}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 ${(- 3 a)}^{3} = - 9 a^{3}$ D、 ${(a b)}^{5} = a^{5} b^{5}$

查看试题解析
5. 如果一个三角形的两边长分别是2和5，则第三边可能是（）

A、2 B、3 C、5 D、8

查看试题解析
6. 在平面直角坐标系中，点 $P (- 2 ， 3)$ 关于y轴对称的点的坐标是（　　）

A、 $(- 2 ， - 3)$ B、 $(2 ， 3)$ C、 $(- 2 ， 3)$ D、 $(2 ， - 3)$

查看试题解析
7. 已知一个多边形的内角和是它的外角和的3倍，则这个多边形是（）

A、八边形 B、七边形 C、六边形 D、五边形

查看试题解析
8. 若 $9 x^{2} + k x + 4$ 是一个关于 $x$ 的完全平方式，那么k值是（）

A、 $\pm 6$ B、 $6$ C、 $\pm 12$ D、 $12$

查看试题解析
9. 如图，在正方形网格中有M，N两点，在直线 $l$ 上求一点P使PM＋PN最短，则点P应选在（）

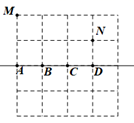A、A点 B、B点 C、C点 D、D点

查看试题解析
10. 如图，已知 $△ A B C$ 是等腰三角形， $B (1, 0)$ ， $∠ A B O = 60 °$ ，点C在坐标轴上，则满足条件的点C的个数是（）

A、8个 B、7个 C、6个 D、5个

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分．

11. 若分式 $\frac{3}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 如图，在 $△ A B C$ 的纸片中， $∠ C = 90 °$ ，沿 $D E$ 剪开得四边形 $A D E B$ ，则 $∠ 1 + ∠ 2$ 的度数为°．

查看试题解析
13. 如图，将一把含有 $45 °$ 角的三角尺的直角顶点放在一张宽 $3 c m$ 的纸带边沿上，另一个顶点放在纸带的另一边沿上，测得三角尺的一直角边与纸带的一边所在的直线成 $30 °$ ，则三角尺的直角边的长为 $c m$ ．

查看试题解析
14. 我们知道，多项式的乘法公式可以利用图形中面积的等量关系来验证其正确性，如 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 就能利用图1的面积进行验证．那么，能利用图2的面积进行验证的含x、y、z的等式为．

查看试题解析
15. 如图，已知 $∠ A C B = ∠ B D A = 90 °$ ，请你添加一个条件，使得 $△ A C B$ ≌ $△ B D A .$ 你添加的条件是： $.$ 写出一个符合题意的即可 $)$

查看试题解析
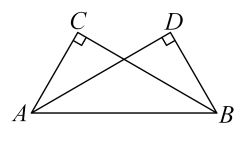16. 运用分式的知识，解决以下问题：
当 $x > 0$ 时，随着x的增大， $\frac{3 x + 2}{x}$ 的值（增大或减小）；
当 $x > 0$ 时，若x无限增大，则 $\frac{3 x + 2}{x}$ 的值无限接近一个数，这个数为．

查看试题解析

三、解答题：本大题共72分，解答应写出文字说明、推理过程或演算步骤．

17. 计算：

(1)、 $2 a^{2} (3 a^{2} + 5 b)$

(2)、 $(5 x + 2 y) (3 x - 2 y)$

查看试题解析
18. 分解因式：

(1)、 $3 a^{2} - 6 a b + 3 b^{2}$ ；

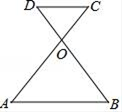
(2)、 $x^{2} (m - 2) + y^{2} (2 - m)$ ．

查看试题解析
19. 如图，已知AC和BD相交于点O，且AB∥DC，OA=OB．
求证：OC=OD．

查看试题解析
20. 为筹办一个大型运动会，某地打算修建一个大型体育中心，已知该地有三个城镇中心（图1中以P ， Q ， R表示）和两条高速公路（图1中以线段PQ ，线段PR表示），在选址过程中，小度同学建议该体育中心所在位置应与该地人口较多的城镇中心P ， Q的距离相等，且到两条高速公路PQ ， PR的距离也相等．请你根据上述小度的建议，试在图2中标出体育中心M的位置．（请保留作图痕迹，不必写作法）

查看试题解析
21. 如图，已知 $A B = D C$ ， $A B ∥ C D$ ， E、F是 $A C$ 上两点，且 $A F = C E$ ．

(1)、求证： $△ A B E ≌ △ C D F$ ；

(2)、若 $∠ B C E = 40 °$ ， $∠ C B E = 60 °$ ，求 $∠ C F D$ 的度数．

查看试题解析
22.

(1)、解分式方程： $\frac{2}{x + 1} - \frac{1}{x} = 0$ ；

(2)、先化简，再求值： $\frac{x^{2} - 1}{x^{2} - 2 x + 1} \div \frac{x + 1}{x - 1} \cdot \frac{1 - x}{x + 1}$ ，其中 $x = 2$ ．

查看试题解析
23. 将 $△ A B C (A B > A C)$ 沿AD折叠，使点C刚好落在AB边上的点E处．

(1)、在图1中，若 $A B = 8$ ， $A C = 6$ ， $S_{△ A C D} = 9$ ，求 $B E$ 和 $△ A B D$ 的面积；

(2)、在图2中，若 $∠ C = 2 ∠ B$ ，求证： $A B = A C + C D$ ．

查看试题解析
24. 列分式方程解下列应用题：

(1)、为响应国家节能减排的号召，某公司计划购买A ， B两种型号的新能源电动汽车．已知A型车比B型车的单价少3万元，且用180万元购买A型车与用240万元购买B型车的数量相等．求A型车的单价．

(2)、用电脑程序控制小型赛车进行 $50 m$ 比赛，“畅想号”和“和谐号”两辆赛车进入了决赛，比赛前的练习中，两辆车从起点同时出发，“畅想号”到达终点时，“和谐号”离终点还差 $2 m$ ．已知“畅想号”的平均速度为 $2.5 m / s$ ．如果两车重新开始比赛，“畅想号”从起点向后退 $2 m$ ，两车同时出发，两车能否同时到达终点？若能，求出两车到达终点的时间；若不能，请说明理由，并调整其中一辆车的平均速度，使两车能同时到达终点．

查看试题解析
25. 如图1，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = a (0 ° < a < 60 °)$ ，将线段 $B C$ 绕点B逆时针旋转 $β (0 ° < β < 180 °)$ 得到线段 $B D$ ．

(1)、如图1，直接写出 $∠ A B D$ 的大小；（用含 $α$ 、 $β$ 的式子表示）

(2)、如图2，当 $β = 60 °$ 时，E为 $△ A B C$ 外的一点， $∠ B C E = 150 °$ ， $∠ A B E = 60 °$ ，判断 $△ A B E$ 的形状，并加以证明．

(3)、若将线段 $B A$ 也绕点B顺时针旋转 $β$ 得到线段 $B E$ ，当C ， D ， E三点在同一条直线上时，请探究 $∠ A D C$ 与 $β$ 的数量关系，并说明理由．

查看试题解析