广东省潮州市2023-2024学年七年级(上)期末数学试卷
试卷更新日期:2024-03-05 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 九章算术中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若收入元记作元,则元表示( )A、收入元 B、收入元 C、支出元 D、支出元2. 地球距太阳约有120000000千米,数120000000用科学记数法表示为( )A、0.12×109 B、1.2×108 C、12×107 D、1.2×1093. 下列各式中,结果是100的是( )A、-(+100) B、-(-100) C、-|+100| D、-|-100|4. 单项式2a2b的系数和次数分别是( )A、2,2 B、2,3 C、3,2 D、4,25. 有理数 , 的对应点在数轴上的位置如图所示,下列结论正确的是( )
 A、 B、 C、 D、6. 若与互补,且 , 则( )A、 B、 C、 D、7. 等式就像平衡的天平,能与如图的事实具有相同性质的是( )
A、 B、 C、 D、6. 若与互补,且 , 则( )A、 B、 C、 D、7. 等式就像平衡的天平,能与如图的事实具有相同性质的是( )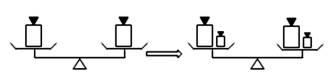 A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么8. 如图,甲从点出发向北偏东方向走到点 , 乙从点出发走到点 , 若 , 则乙从点出发沿方向走到点 . ( )
A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么8. 如图,甲从点出发向北偏东方向走到点 , 乙从点出发走到点 , 若 , 则乙从点出发沿方向走到点 . ( ) A、南偏西 B、西偏南 C、南偏西 D、西偏南9. 如图是一个计算程序,若输入 的值为-1,则输出的结果 为( )
A、南偏西 B、西偏南 C、南偏西 D、西偏南9. 如图是一个计算程序,若输入 的值为-1,则输出的结果 为( ) A、-5 B、-6 C、5 D、610. 某班级劳动时,将全班同学分成个小组,若每小组人,则余下人;若每小组人,则有一组少人.按下列哪个选项重新分组,能使每组人数相同?( )A、组 B、组 C、组 D、组
A、-5 B、-6 C、5 D、610. 某班级劳动时,将全班同学分成个小组,若每小组人,则余下人;若每小组人,则有一组少人.按下列哪个选项重新分组,能使每组人数相同?( )A、组 B、组 C、组 D、组二、填空题:本题共6小题,每小题3分,共18分。
-
11. 比较大小: .12. 如果和是同类项,那么 .13. 如图,已知线段 , 延长线段到 , 使 , 那么 .
 14. 如图是一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则 .
14. 如图是一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则 . 15. 若 , 则的值为 .16. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
15. 若 , 则的值为 .16. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为 .
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为 . 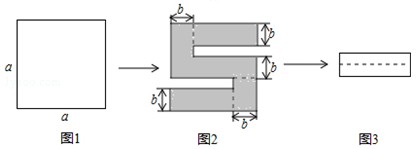
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算:(1)、;(2)、 .18. 解方程: .19. 尺规作图不写作法,保留作图痕迹
已知:如图点 , 点 , 点 .
 (1)、作直线;(2)、作线段;(3)、作射线 , 并在射线上截取 .20. 先化简,再求值
(1)、作直线;(2)、作线段;(3)、作射线 , 并在射线上截取 .20. 先化简,再求值, 其中 , .
21. 在年卡塔尔世界杯比赛中,参赛队伍为支,比赛采取单循环方式在小组赛中,积分规则如下:胜一场球队积分,平一场积分,负一场积分组积分榜信息如表所示:球队名称
场次
胜场
平场
负场
总积分
阿根廷
波兰
墨西哥
沙特阿拉伯
(1)、沙特阿拉伯在场小组赛中总积分是 ;(2)、根据组积分榜信息,求阿根廷在场小组赛中胜场的场数.22. “滴滴司机”沈师傅从上午:至:在东西方向的人民路上营运,共连续运载十批乘客,若规定向东为正,向西为负,沈师傅运十批乘客里程如下:单位:千米, , , , , , , , ,
(1)、将最后一批乘客送到目的地,沈师傅能回到出发点吗?(2)、若汽车每千米耗油升,则:至:汽车共耗油多少升?(3)、若“滴滴”的收费标准为:起步价元不超过千米;若超过千米,则超过部分按每千米元收费,现有一名乘客共付车费元,则这名乘客共乘坐了多少千米?23. 如图所示,是一列用若干根火柴棒摆成的由正方形组成的图案. (1)、完成下表的填空:
(1)、完成下表的填空:正方形个数
火柴棒根数
(2)、某同学用若干根火柴棒按如上图列的方式摆图案,摆完了第个后,摆第个,接着摆第个,第个, , 当他摆完第其中一个图案时剩下了根火柴棒,要刚好摆完下一个图案还差根,没办法完成问最后摆完的图案是第几个图案?24. 如图 , 直角三角板的直角顶点在直线上, , 是三角板的两条直角边,射线是的平分线. (1)、当时,求的度数;(2)、当时,求的度数;(3)、当时,则用含的式子表示;(4)、当三角板绕点逆时针旋转到图位置时, , 其它条件不变,则用含的式子表示 .25. 如图,数轴上、两点对应的数分别为、 , 点为数轴上一动点,点对应的数为 .
(1)、当时,求的度数;(2)、当时,求的度数;(3)、当时,则用含的式子表示;(4)、当三角板绕点逆时针旋转到图位置时, , 其它条件不变,则用含的式子表示 .25. 如图,数轴上、两点对应的数分别为、 , 点为数轴上一动点,点对应的数为 . (1)、填空:若时,点到点、点的距离之和为 .(2)、填空:若点到点、点的距离相等,则 .(3)、填空:若 , 则 .(4)、若动点以每秒个单位长度的速度从点向点运动,动点以每秒个单位长度的速度从点向点运动,两动点同时运动且一动点到达终点时另一动点也停止运动,经过秒 , 求的值.
(1)、填空:若时,点到点、点的距离之和为 .(2)、填空:若点到点、点的距离相等,则 .(3)、填空:若 , 则 .(4)、若动点以每秒个单位长度的速度从点向点运动,动点以每秒个单位长度的速度从点向点运动,两动点同时运动且一动点到达终点时另一动点也停止运动,经过秒 , 求的值.