广东省佛山市顺德区2023-2024学年七年级(上)期末数学试卷
试卷更新日期:2024-03-05 类型:期末考试
一、选择题(10个题,每题3分,共30分)
-
1. 的相反数是A、2 B、 C、 D、2. 为了完成下列任务,最适合采用全面调查的是A、了解我国七年级学生的视力情况 B、了解一批电视机的寿命 C、了解顺德学生的“垃圾分类”意识 D、了解某中学教师的身体健康状况3. 木星的赤道半径约为71400000米,将71400000用科学记数法表示为A、 B、 C、 D、4. 下列图形经过折叠不可以得到正方体的是A、
 B、
B、 C、
C、 D、
D、 5. 关于单项式 , 下列说法中正确的是A、次数是3 B、次数是2 C、系数是 D、系数是6. 已知是方程的解,则的值为A、 B、4 C、3 D、7. 下列计算正确的是A、 B、 C、 D、8. 如图,能用、、三种方法表示同一个角的是A、
5. 关于单项式 , 下列说法中正确的是A、次数是3 B、次数是2 C、系数是 D、系数是6. 已知是方程的解,则的值为A、 B、4 C、3 D、7. 下列计算正确的是A、 B、 C、 D、8. 如图,能用、、三种方法表示同一个角的是A、 B、
B、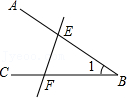 C、
C、 D、
D、 9. 有理数 , 在数轴上对应的点如图所示.下列结论:①;②;③;④ , 其中正确的是
9. 有理数 , 在数轴上对应的点如图所示.下列结论:①;②;③;④ , 其中正确的是 A、①②③ B、①③④ C、②④ D、①②③④10. 如图,为长方形纸片的边上一点,将纸片沿折叠,点落在点处,将纸片沿折叠,点落在点处.若 , 则
A、①②③ B、①③④ C、②④ D、①②③④10. 如图,为长方形纸片的边上一点,将纸片沿折叠,点落在点处,将纸片沿折叠,点落在点处.若 , 则 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(5个题,每题3分,共15分)
-
11. 比较大小:(填“”或“”12. 合并同类项: .13. 用棋子摆成如图所示的“”形图.按这样的规律摆下去,第6个“”字有 个棋子.
 14. 若从边形的一个顶点出发,可以画出4条对角线,则的值是 ,15. 如图是一个几何体,请你描述这个几何体的特点(写出三点) .
14. 若从边形的一个顶点出发,可以画出4条对角线,则的值是 ,15. 如图是一个几何体,请你描述这个几何体的特点(写出三点) .
三、解答题(8个题,共75分)
-
16. 计算: .17. 学校七年级的学生对老年人处理生病问题的方式进行了调查: . 子女陪同去医院就诊; . 独自去医院就诊; . 自己在家里服用备用药; . 请人帮忙购药; . 其它.发出60份问卷全部收回,均为有效问卷,将调查结果整理如下:
方式
人数
6
18
24
9
3
 (1)、补全条形统计图;(2)、画出扇形统计图.18. 已知 , .(1)、化简:;(2)、若与互为相反数,当 , 时,求的值.19. 某商场购进、两款服装共100件,其中款服装每件的进价比款服装每件的进价多50元,购进款服装4件与购进款服装5件的进价相同.(1)、求每件款服装的进价是多少元?(2)、款服装每件的利润率为 , 款服装按进价提高后标价,又以9折销售.所有服装全部售完总获利为2960元,求款服装购进多少件?(参考公式:利润进价利润率)20. 综合与实践
(1)、补全条形统计图;(2)、画出扇形统计图.18. 已知 , .(1)、化简:;(2)、若与互为相反数,当 , 时,求的值.19. 某商场购进、两款服装共100件,其中款服装每件的进价比款服装每件的进价多50元,购进款服装4件与购进款服装5件的进价相同.(1)、求每件款服装的进价是多少元?(2)、款服装每件的利润率为 , 款服装按进价提高后标价,又以9折销售.所有服装全部售完总获利为2960元,求款服装购进多少件?(参考公式:利润进价利润率)20. 综合与实践幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方.
 (1)、观察三阶幻方,每行、每列、每条对角线上的三个数的数量关系是 ;若将正中间的数记为 , 则9个数的和可表示为 (用含的代数式表示);(2)、将 , 0,10,2,8, , 6, , 4分别填入图1中,构成一个三阶幻方;(3)、根据图2的幻方,求出的值.21. 如图,点是线段上一点.在射线上截取 , 在射线上截取 .
(1)、观察三阶幻方,每行、每列、每条对角线上的三个数的数量关系是 ;若将正中间的数记为 , 则9个数的和可表示为 (用含的代数式表示);(2)、将 , 0,10,2,8, , 6, , 4分别填入图1中,构成一个三阶幻方;(3)、根据图2的幻方,求出的值.21. 如图,点是线段上一点.在射线上截取 , 在射线上截取 . (1)、用尺规作图法作出符合题意的图形(保留作图痕迹,不需要写作法);(2)、若 , .
(1)、用尺规作图法作出符合题意的图形(保留作图痕迹,不需要写作法);(2)、若 , .①求的长;
②若 , 探究的长;
(3)、连接 , 在四边形内找一点 , 使它到、、、四个顶点的距离之和最小,并说明理由.22. 综合运用如图,数轴上两点、对应的数分别是和8.点从点出发,以每秒2个单位长度的速度沿数轴正方向匀速运动,设的运动时间为秒.
 (1)、、两点的距离为 ;(2)、当运动到的中点时,求的值;(3)、若一动点同时从点出发,以每秒5个单位长度的速度沿数轴负方向匀速运动,当点到达点时,、两点都停止运动.在此过程中,当时,求的值.23. 综合探究
(1)、、两点的距离为 ;(2)、当运动到的中点时,求的值;(3)、若一动点同时从点出发,以每秒5个单位长度的速度沿数轴负方向匀速运动,当点到达点时,、两点都停止运动.在此过程中,当时,求的值.23. 综合探究将两块三角板如图1所示放置,∠ACB=90°,∠BAC=45°,∠CDE=90°,∠DCE=30°,AC=CD=6.将△DCE 绕着点C顺时针旋转时CF平分∠BCD.
 (1)、如图1,当CD边与CA边重合时,求∠ECF的度数;(2)、如图2,在旋转过程中,当∠ACD=2∠ECF时,求线段CD扫过的面积(结果保留π);(3)、当边CD与CB重合时停止旋转,探究∠ACD与∠ECF满足的数量关系,并说明理由.
(1)、如图1,当CD边与CA边重合时,求∠ECF的度数;(2)、如图2,在旋转过程中,当∠ACD=2∠ECF时,求线段CD扫过的面积(结果保留π);(3)、当边CD与CB重合时停止旋转,探究∠ACD与∠ECF满足的数量关系,并说明理由.