广东省深圳市福田区重点学校2023-2024学年九年级下学期开学考试数学试题
试卷更新日期:2024-03-05 类型:开学考试
一、选择题(共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)
-
1. 如图所示的几何体的左视图为( )
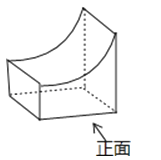 A、
A、 B、
B、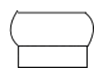 C、
C、 D、
D、 2. 随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.0000034m,用科学记数法表示0.0000034是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 从思想政治、地理、化学、生物4门再选科目中选择2门参加考试,选到地理的概率是( )A、 B、 C、 D、5. 为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:
2. 随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯是现在世界上最薄的纳米材料,其理论厚度应是0.0000034m,用科学记数法表示0.0000034是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 从思想政治、地理、化学、生物4门再选科目中选择2门参加考试,选到地理的概率是( )A、 B、 C、 D、5. 为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:锻炼时间(时)
3
4
5
6
7
人数(人)
6
13
14
5
2
这40名居民一周体育锻炼时间的众数和中位数是( )
A、14,5 B、5,5 C、14,6 D、5,66. 随着生活水平的提高和环保意识的增强,小亮家购置了新能源电动汽车,这样他乘电动汽车比乘公交车上学所需的时间少用了15分钟,已知电动汽车的平均速度是公交车的2.5倍,小亮家到学校的距离为8千米.若设乘公交车平均每小时走x千米,则可列方程为( )A、 B、 C、 D、7. 由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正切值为( )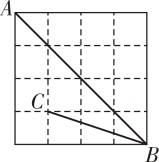 A、 B、 C、 D、8. 如图,将△ABC的AB边与刻度尺的边缘重合,点A,D,B分别对应刻度尺上的整数刻度.已知 , , , 下列结论不正确的是( )
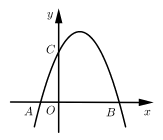
A、 B、 C、 D、8. 如图,将△ABC的AB边与刻度尺的边缘重合,点A,D,B分别对应刻度尺上的整数刻度.已知 , , , 下列结论不正确的是( ) A、 B、 C、 D、9. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:
A、 B、 C、 D、9. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:① ;②当 时,y随x的增大而增大;③ ;④ .
其中正确的个数有( )
 A、1个 B、2个 C、3个 D、4个10. 如图,在正方形ABCD中,M是边CD上一点,满足 , 连接BM交AC于点N,延长BN到点P使得 , 则( )
A、1个 B、2个 C、3个 D、4个10. 如图,在正方形ABCD中,M是边CD上一点,满足 , 连接BM交AC于点N,延长BN到点P使得 , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共5小题,每小题3分,共15分)
-
11. 因式分解= .12. 如图,抛物线的顶点为A,与y轴交于点B,则直线AB的表达式为 .
 13. 如图,小山的东侧炼A处有一个热气球,由于受西风的影响,以30(米/分)的速度沿与地面成75°角的方向飞行,20分后到达点C处,此时热气球上的人测得小山西侧点B处的俯角为30°,则小山东西两侧A,B两点间的距离为米(结果保留根号).
13. 如图,小山的东侧炼A处有一个热气球,由于受西风的影响,以30(米/分)的速度沿与地面成75°角的方向飞行,20分后到达点C处,此时热气球上的人测得小山西侧点B处的俯角为30°,则小山东西两侧A,B两点间的距离为米(结果保留根号).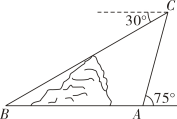 14. 如图,A,B是函数上两点,P为一动点,作轴,轴,若 , 则 .
14. 如图,A,B是函数上两点,P为一动点,作轴,轴,若 , 则 .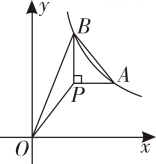 15. 如图,正方形ABCD中,点E.F分别在边BC,CD上,AB=6, , 连接BD交AF于点N,交AE于点M,若 , 则DN为 .
15. 如图,正方形ABCD中,点E.F分别在边BC,CD上,AB=6, , 连接BD交AF于点N,交AE于点M,若 , 则DN为 .
三、计算题(共7小题,共55分)
-
16. 计算: .17. 先化简,再求值: , 其中x在-2,-1,0,2四个数中选取一个合适的数代入.18. 为了打造书香文化,培养阅读习惯.崇德中学计划在各班建图书角,开展“我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
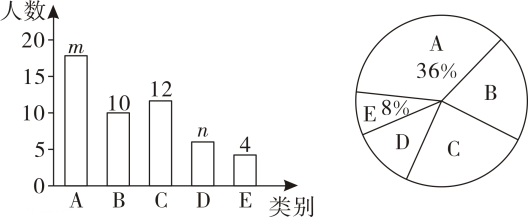
根据图中信息,请回答下列问题;
(1)、条形图中的m= , n= ,(2)、文学类书籍对应扇形圆心角等于度:(3)、若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;(4)、甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.19. 某网店以每个32元的价格购进了一批玩具,由于销售火爆,销售单价经过两次的调整,从每个50元上涨到每个72元,此时每天可售出200个玩具.(1)、若销售价格每次上涨的百分率相同,求每次上涨的百分率;(2)、经过市场调查发现:销售单价每降价1元,每天多卖出10个,网店每个应降价多少元?才能使每天利润达到最大,最大利润为多少元?20. 如图,中, , 分别以点B,C为圆心,以大于的长为半径画弧交于M,N两点,作直线MN交BC于点O,连接AO并延长,交DC的延长线于点E,连接AC,BE. (1)、求证::(2)、在中能否添加一个条件,使四边形ABEC为菱形?若能,请添加后予以证明;若不能,请什么理由.21. 已知抛物线(a、b、c是常数,a≠0),自变量x与函数值y的部分对应值如表:
(1)、求证::(2)、在中能否添加一个条件,使四边形ABEC为菱形?若能,请添加后予以证明;若不能,请什么理由.21. 已知抛物线(a、b、c是常数,a≠0),自变量x与函数值y的部分对应值如表:x
0
1 2 3
……
y
-2
m -2 1
……
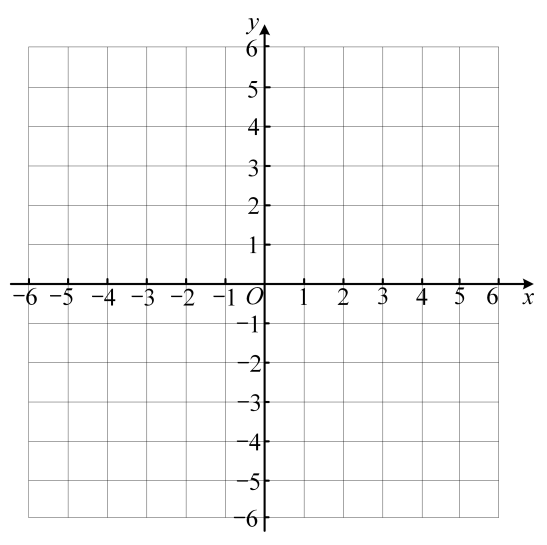
(1)、根据以上信息,可知抛物线开口向 , 对称轴为直线 .(2)、求抛物线的解析式和m的值.(3)、将抛物线的图象记为 , 将绕点O旋转180°后的图象记为 , 、合起来得到的图象记为G,完成以下问题:①画出G的图像
②若直线与函数G有且只有两个交点,直接写出k的取值范围_▲__.
 22. 在正方形ABCD中,点G是边AB上的一个动点,点F、E在边BC上, , 且、GF、DE的延长线相交于点P.
22. 在正方形ABCD中,点G是边AB上的一个动点,点F、E在边BC上, , 且、GF、DE的延长线相交于点P. (1)、如图1,当点E与点C重合时,的度数=;(2)、如图2,当点E与C不重合时,在点G的运动过程中,的度数是否发生变化,若不变,求出的度数,若变化,请说明理由(3)、在(2)的条件下,如图3,过D作于点N,连接CN.BP,取BP的中点M,连接MN,在点G的运动过程中,求的值(直接写出结果即可).
(1)、如图1,当点E与点C重合时,的度数=;(2)、如图2,当点E与C不重合时,在点G的运动过程中,的度数是否发生变化,若不变,求出的度数,若变化,请说明理由(3)、在(2)的条件下,如图3,过D作于点N,连接CN.BP,取BP的中点M,连接MN,在点G的运动过程中,求的值(直接写出结果即可).