贵州省黔东南州教学资源共建共享实验基地名校2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-03-05 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 一元二次方程的一次项系数是( )A、 B、 C、 D、2. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片
3. 下列事件是必然事件的是( )A、打开电视机,正在播放动画片
B、太阳每天从东方升起
C、某彩票中奖率是 , 买张一定会中奖 D、某运动员跳高的最好成绩是米4. 点关于原点对称的点的坐标是( )A、 B、 C、 D、5. 二次函数的顶点坐标是( )A、 B、 C、 D、6. 如图,为等边三角形,是内一点,若将经过旋转到的位置,则旋转角的度数为( )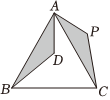 A、 B、 C、 D、7. 如图,AB是⊙O的直径,BC是⊙O的弦,已知∠AOC=80°,则∠ABC的度数为( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,BC是⊙O的弦,已知∠AOC=80°,则∠ABC的度数为( ) A、20° B、30° C、40° D、50°8. 关于的方程的一根是 , 则的值是( )A、 B、 C、 D、9. 一次函数与二次函数在同一坐标系中的大致图象可能是( )A、
A、20° B、30° C、40° D、50°8. 关于的方程的一根是 , 则的值是( )A、 B、 C、 D、9. 一次函数与二次函数在同一坐标系中的大致图象可能是( )A、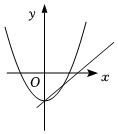 B、
B、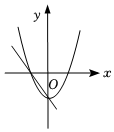 C、
C、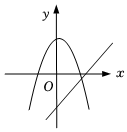 D、
D、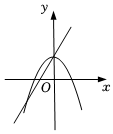 10. 如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )
10. 如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( ) A、5cm B、5cm C、5cm D、6cm11. 如图,正三角形的边长为 , , , 分别为 , , 的中点,以 , , 三点为圆心,长为半径作圆.则图中阴影部分的面积为( )
A、5cm B、5cm C、5cm D、6cm11. 如图,正三角形的边长为 , , , 分别为 , , 的中点,以 , , 三点为圆心,长为半径作圆.则图中阴影部分的面积为( ) A、 B、 C、 D、12. 二次函数中,自变量与函数的对应值如下表:
A、 B、 C、 D、12. 二次函数中,自变量与函数的对应值如下表:若 , 则下面叙述正确的是( )
A、该函数图象开口向上
B、该函数图象与轴的交点在轴的下方 C、对称轴是直线 D、若是方程的正数解,则二、填空题:本题共4小题,每小题4分,共16分。
-
13. 一天中钟表时针从上午时到上午时旋转的度数为 .14. 抛物线可以由抛物线向 平移个单位得到.15. 设 , 是一元二次方程的两根,则 .16. 在矩形中, , , 点是平面内一动点,且满足 , 为的中点,点运动过程中线段长度的取值范围是 .

三、解答题:本题共9小题,共98分。解答应写出文字说明,证明过程或演算步骤。
-
17. 解方程:
(1)、;
(2)、 .18. 如图,二次函数的图象与轴交于、两点,对称轴是轴,利用图象解答下列问题: (1)、点、的坐标分别是: , ;(2)、若 , 则的取值范围是 ;(3)、函数的最小值是 .19. 在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个. 现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.20. 如图,是的外接圆,是的直径,于点 .
(1)、点、的坐标分别是: , ;(2)、若 , 则的取值范围是 ;(3)、函数的最小值是 .19. 在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个. 现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.20. 如图,是的外接圆,是的直径,于点 .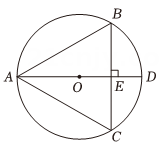 (1)、求证:;(2)、连接并延长,交于点 , 连接 , 若 , 求的长.21. 某扶贫单位为了提高贫困户的经济收入,购买了的铁栅栏,准备用这些铁栅栏为贫困户靠墙墙长围建一个中间带有铁栅栏的矩形养鸡场如图所示 .
(1)、求证:;(2)、连接并延长,交于点 , 连接 , 若 , 求的长.21. 某扶贫单位为了提高贫困户的经济收入,购买了的铁栅栏,准备用这些铁栅栏为贫困户靠墙墙长围建一个中间带有铁栅栏的矩形养鸡场如图所示 . (1)、若要建的矩形养鸡场面积为 , 求鸡场的长和宽;(2)、该扶贫单位想要建一个的矩形养鸡场,这一想法能实现吗?请说明理由.22. 如图,中,点在边上. , 将线段绕点旋转到的位置使得连接 , 与交于点 .
(1)、若要建的矩形养鸡场面积为 , 求鸡场的长和宽;(2)、该扶贫单位想要建一个的矩形养鸡场,这一想法能实现吗?请说明理由.22. 如图,中,点在边上. , 将线段绕点旋转到的位置使得连接 , 与交于点 . (1)、求证:;
(1)、求证:;
(2)、若 , , 的度数为23. 某公司以每件元的价格购进一种商品,在销售过程中发现这种商品每天的销售量件与每件的销售单价元满足一次函数关系: .(1)、当时,总利润为元;
(2)、若设总利润为元,则与的函数关系式是;
(3)、若每天的销售量不少于件,则销售单价定为多少元时,此时利润最大,最大利润是多少?24. 如图,抛物线交轴于、两点,交轴于 , 点在抛物线上,横坐标设为 . (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、当点在轴上方时,直接写出的取值范围;
(3)、若抛物线在点右侧部分含点的最高点的纵坐标为 , 求的值.25. 如图,在Rt△ABC中,∠BAC=90°,AB=AC . 在平面内任取一点D , 连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE , 连结DE , CE , BD . (1)、请根据题意补全图1;(2)、猜测BD和CE的数量关系并证明;(3)、作射线BD , CE交于点P , 把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
(1)、请根据题意补全图1;(2)、猜测BD和CE的数量关系并证明;(3)、作射线BD , CE交于点P , 把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.