贵州省毕节市七星关区第四教育集团2023-2024学年八年级上学期数学期末考试试卷

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题（共15小题，满分45分，每小题3分）

1. 下列各数：3.14，﹣2， $\frac{1}{π}$ ， 0，2 $\sqrt{5}$ ， 0.6，其中无理数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列曲线中不能表示y是x的函数的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列二次根式中，最简二次根式是（　　）

A、 $\sqrt{2}$ B、 $\sqrt{4}$ C、 $\sqrt{\frac{a}{2}}$ D、 $\sqrt{x^{3}}$

查看试题解析
4. 下列各组数中不是勾股数的是（）

A、9，15，12 B、11，60，61 C、6，8，10 D、0.3，0.4，0.5

查看试题解析
5. 已知x ， y为正整数，且x $＜ \sqrt{8} ＜$ y ，则y^x的最小值为（　　）

A、1 B、3 C、4 D、9

查看试题解析
6. 已知点A（1，y₁）和点B（a ， y₂）在一次函数y＝﹣2x+b的图象上，且y₁＞y₂ ，则a的值可能是（　　）

A、2 B、0 C、﹣1 D、﹣2

查看试题解析
7. 如图，是一次函数y＝kx+b+1的图象，则下列结论正确的是（　　）

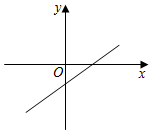A、k＜0，b＜0 B、k＞0，b＜﹣1 C、k＞0，b＜0 D、k＜0，b＞﹣1

查看试题解析
8. 函数y＝﹣kx+1（k≠0）的图象如图所示，则方程kx＝1的解是（　　）

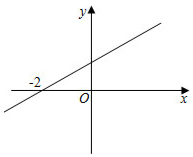A、x＝﹣2 B、x＝﹣1 C、x＝0 D、x＝1

查看试题解析
9. 一次函数y＝kx+2的图象绕着原点逆时针旋转90°后，经过点（﹣1，﹣3），则k的值为（　　）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、﹣1 D、1

查看试题解析
10. 如图，一次飓风灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，那么这棵树折断之前的高度是（　　）

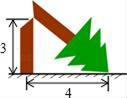A、5米 B、6米 C、7米 D、8米

查看试题解析
11. 在平面直角坐标系中，方程2x+3y＝4所对应的直线为a ，方程3x+2y＝4所对应的直线为b直线a与b的交点为P（m ， n），下列说法错误的是（　　）

A、 $\{\begin{array}{l} x = m \\ y = n \end{array}$ 是方程2x+3y＝4的解 B、 $\{\begin{array}{l} x = m \\ y = n \end{array}$ 是方程3x+2y＝4的解 C、 $\{\begin{array}{l} x = m \\ y = n \end{array}$ 是方程组 $\{\begin{array}{l} 2 x + 3 y = 4 \\ 3 x + 2 y = 4 \end{array}$ 的解 D、以上说法均错误

查看试题解析
12. 在平面直角坐标系中，有A（﹣2，a+2），B（a﹣3，4）两点，若AB∥x轴，则A ， B两点间的距离为（　　）

A、2 B、1 C、4 D、3

查看试题解析
13. 若实数m ， n ， p ， q在数轴上的对应点的位置如图所示，且n与q互为相反数，则绝对值最大的数对应的点是（）

A、点M B、点N C、点P D、点Q

查看试题解析
14. 如图，平面直角坐标系中A（﹣4，0），C（1，0），以点A为圆心，AC长为半径画弧，交y轴正半轴于点B ，则点B的坐标为（　　）

A、（0，3） B、（3，0） C、（2，0） D、（0，2）

查看试题解析
15. 如图，在等边△ABC中，AD⊥BC于D ，延长BC到E ，使 $C E = \frac{1}{2} B C$ ， F是AC的中点，连接EF并延长EF交AB于G ， BG的垂直平分线分别交BG ， AD于点M ，点N ，连接GN ， CN ，下列结论：①∠ACN＝∠BGN；② $G F = \frac{1}{2} E F$ ；③∠GNC＝120°；④GM＝CN；⑤EG⊥AB ，其中正确的个数是（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（共5小题，满分25分，每小题5分）

16. 化简： $\sqrt{16} =$ ．

查看试题解析
17. 如果 $\sqrt{x - 6}$ 有意义，那么x的取值范围是．

查看试题解析
18. 对于任意不相等的两个正实数a ， b ，定义运算△如下：如a△b $= \frac{\sqrt{a + b}}{3 - 2}$ ，如3△2 $= \frac{\sqrt{3 + 2}}{3 - 2} = \sqrt{5}$ ，那么8△12＝．

查看试题解析
19. 蝴蝶标本可以近似地看作是轴对称图形，如图，将一只蝴蝶标本放在平面直角坐标系中，如果点B的坐标是（﹣3，2），那么它关于y轴对称的点A的坐标是．

查看试题解析
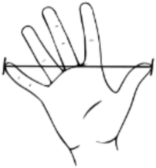
20. 如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．根据最近人体构造学的研究成果表明，一般情况下，人的指距d和身高h成某种关系．如表是测得的指距与身高的一组数据：
指距d/厘米
20
21
22
23
身高h/厘米
160
169
178
187
根据如表解决下面这个实际问题：姚明的身高是226厘米，可预测他的指距约为厘米．（结果精确到0.1）

查看试题解析

三、解答题（共7小题，满分80分）

21.

(1)、计算： $\sqrt{18} - \frac{2}{\sqrt{2}} +$ |1 $- \sqrt{2}$ |+（ $\frac{1}{2}$ ）^﹣1

(2)、解方程组： $\{\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$ ．

查看试题解析
22. 观察下面的变形规律：
$\frac{1}{\sqrt{2} + 1}$ ＝ $\sqrt{2}$ －1， $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\sqrt{3}$ － $\sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}}$ ＝ $\sqrt{4}$ － $\sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}}$ ＝ $\sqrt{5}$ － $\sqrt{4}$ ，…

解答下面的问题：

(1)、若 $n$ 为正整数，请你猜想 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝；

(2)、计算： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2016} + \sqrt{2015}}) \times (\sqrt{2016} + 1)$

查看试题解析
23. 已知，在平面直角坐标系中有△ABC ．
C（﹣2，0），B（﹣6，0），A（﹣4，8）

(1)、若△ABC沿y轴正方向平移2个单位得到△A₁B₁C₁ ，画出图形并写出各点的坐标；

(2)、作△A₁B₁C₁关于x轴对称的△A₂B₂C₂ ，并写出各点的坐标．

查看试题解析
24. 如图是某沿江地区交通平面图，其中，MN⊥ON ， OP⊥QP ．为了加快经济发展，该地区拟修建一条连接M ， O ， Q三个城市的沿江高速公路，已知该沿江高速公路的建设成本是100万元/km ，该沿江高速公路的造价预计是多少？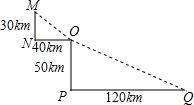

查看试题解析
25. 台风是一种自然灾害，它在以台风中心为圆心，一定长度为半径的圆形区域内形成极端气候，有极强的破坏力．如图，监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动，已知点C为一海港，且点C与A ， B两点的距离分别为300km、400km ，且∠ACB＝90°，过点C作CE⊥AB于点E ，以台风中心为圆心，半径为260km的圆形区域内为受影响区域．

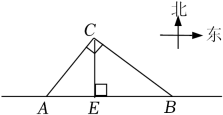(1)、求监测点A与监测点B之间的距离；

(2)、请判断海港C是否会受此次台风的影响，并说明理由；

(3)、若台风的速度为25km/h ，则台风影响该海港多长时间

查看试题解析
26. 为迎接党的二十大，助力乡村振兴，实现群众增产增收，某商场设立专柜，在乡村地区直接采购农副产品，架起对口农户与消费者之间的桥梁，实现农副产品直产直销．该专柜负责人欲查询两种商品的进货数量，发现进货单已被墨水污染．
进货单
商品
进价/（元/件）
数量/件
金额/元
绩溪山核桃
45
黄山毛峰
75
商品采购员李经理对采购情况回忆如下：两种商品共采购了100件．

(1)、若采购花费的总金额为5700元，问绩溪山核桃和黄山毛峰的进货数量分别为多少？

(2)、在进价不变的情况下，由于市场火爆，该专柜负责人计划再次安排采购这两种商品共100件，假设黄山毛峰的进货数量为x（件），所花费的总金额为y（元）．
①求出y与x的函数关系式；
②若李经理用不超过5000元采购这两种商品，问他最多能购买黄山毛峰多少件？

(3)、若绩溪山核桃每件的售价为80元，黄山毛峰每件的售价为100元，商场规定黄山毛峰的进货数是为a（35≤a≤40）件，请问应怎样进货才能使商场在销售完这批货物时获利最多？此时利润为多少元？

查看试题解析
27. 【模型建立】如图，等腰直角三角形ABC中∠ACB＝90°，CB＝CA ，直线ED经过点C ，过点A作AD⊥ED于点D ，过点B作BE⊥ED于点E ，易证明△BEC≌△CDA ，我们将这个模型称为“K形图”．
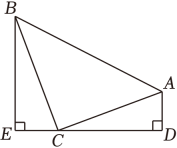
【模型应用】

(1)、如图1，当点A（﹣2，0），B（0，4）在坐标轴上时，连接AB ，以AB为直角边，点B为直角顶点作等腰直角三角形ABC ，则点C的坐标为；

(2)、应用：如图2，在四边形ABCD中，∠ADC＝90°，AD＝6，CD＝8，BC＝10，AB $= 10 \sqrt{2}$ ．求线段BD的长；

(3)、如图3，已知直线y＝﹣2x+4与坐标交于A、B两点，点D的坐标为（6，0），若直线AB上有一点M ，使∠BMD＝45°，求线段BM的长度．

查看试题解析

商品	进价/（元/件）	数量/件	金额/元
绩溪山核桃	45
黄山毛峰	75

指距d/厘米	20	21	22	23
身高h/厘米	160	169	178	187