广东省汕头市龙湖区2023~2024学年九年级第一学期数学期末学生学业质量评估
试卷更新日期：2024-03-04 类型：期末考试
一、选择题（本大题10小题，每小题3分，共30分，每小题给出四个选项中只有一个是正确的）
-
1. 我国传统文化中的“福禄寿喜”图(如图)由四个图案构成，这四个图案中是中心对称图形的是（ ）A、
B、
C、
D、
2. 若关于x的方程(m+2)x2-3x+1=0是一元二次方程，则m的取值范围是（ ）A、m≠0 B、m>-2 C、m≠-2 D、m>03. 有一个摊位游戏，先旋转一个转盘的指针，如果指针箭头停在奇数的位置，玩的人可以从袋子里抽出一个弹珠，当摸到黑色的弹珠就能得到奖品，转盘和弹珠如图所示，小明玩了一次这个游戏，则小明得奖的可能性为（ ）
A、不可能 B、不太可能 C、非常有可能 D、一定可以4. 在反比例函数图象的每一支上，y都随x的增大而增大.则k的取值范围是（ ）A、 B、 C、 D、5. 关于一元二次方程根的情况，下列说法中正确的是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 在半径为 的圆中，60°的圆心角所对弧的弧长是（ ）A、 B、 C、 D、7. 顶点（-5，-1），且开口方向、形状与函数y=-x2的图象相同的抛物线的是（ ）A、y= (x -5)x2+1 B、y=-x2-5 C、y=-(x +5)x2-1 D、y= (x -5)x2-18. 如图，在⊙O中， ， . 则 的度数为（ ）
A、 B、 C、 D、9. 第二十二届世界杯足球赛于2022年11月20日在卡塔尔举办开幕赛，为了迎接世界杯，某市举行了足球邀请赛，规定参赛的每两支球队之间比赛一场，共安排了45场比赛.设比赛组织者邀请了x个队参赛，则下列方程正确的是（ ）A、x (x +1)=45 B、 x (x - 1)=45 C、 x (x +1)=45 D、x (x - 1)=4510. 如图，抛物线y=ax2+bx+c的图象与x轴交于A（-1，0），B 两点与y轴交于点C，对称轴为x=1，则下列四个结论：①ac<0；②2a+b=0；③-1<x<3 时，y>0；④4a+c<0.其中正确结论的个数为（ ）
A、1个 B、2个 C、3个 D、4个二、填空题（本大题共 5 小题，每题 3分，共15分）将正确答案写在答题卡相应的位置上.
-
11. 如图，四角星的顶点是一个正方形的四个顶点，将这个四角星绕其中心旋转，当第一次与自身重合时，其旋转角的大小是度．
12. 如图，圆锥形烟囱帽的底面直径为80cm，母线长为50cm，则这样的烟囱帽的侧面积是。
13. 将抛物线y=-2(x -1)2+3向上平移2个单位，得到的抛物线是。14. 如图，在同一平面直角坐标系中，直线 y=t（t为常数）与反比例函数，y1= ， y2=﹣的图象分别交于点A，B，点O为坐标原点，连接OA，OB，则△OAB的面积为
15. 如图，在△ABC中，∠C＝90°，AC＝8，AB＝10，D是AC上一点，且CD＝3，E是BC边上一点，将△DCE沿DE折叠，使点C落在点F处，连接BF，则BF的最小值为 ．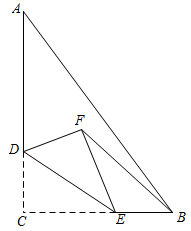
三、解答题（一）（本大题4小题，第16、17题各5分，第18、19题各7分，共24分）
-
16. 解方程：x2+6x+5=0．17. 如图△ABC三个顶点的坐标分别为A（1，1），B（4，2）C（3，4）.请画出 △ABC关于原点O对称的图形△A1B1C1并写出点B1的坐标.
18. 已知关于x的方程x2-kx +k-1=0.(1)、方程有一根为2，求k的值；(2)、求证：不论k为何值，方程总有实数根.19. 如图，在平面直角坐标系中，一次函数y=kx+b与反比例函数y=﹣的图象交于A（﹣1，6），B（m，﹣3）两点，一次函数 y= kx +b 的图象与y轴交于点C.
(1)、求一次函数的解析式；(2)、根据函数的图象，直接写出不等式kx+b≤﹣的解集；四、解答题（二）（本大题3小题，每小题9分，共27分）
-
20. 在定西这块深沉的土地上，处处彰显着文化的韵味.如石器时代的马家窑文化、齐家文化，青铜时代的辛店文化，寺洼文化，现有四张不透明的卡片，它们的背面完全一样，正面分别写有马家窑文化、齐家文化、辛店文化、寺洼文化，将四张卡片背面朝上，洗匀后放在桌子上.
(1)、从中随机抽取一张，抽到“辛店文化”的概率为；(2)、从中随机抽取一张（不放回），接着再随机抽取一张，请通过画树状图或列表法，求抽到的两张卡片所写的都属于石器时代文化的概率。21. 某商店销售一款工艺品，每件成本为元，为了合理定价，投放市场进行试销．据市场调查，销售单价是元时，每月的销售量是件，而销售单价每降价元，每月可多销售件．设这种工艺品每件降价x元．(1)、每件工艺品的实际利润为元（用含有x的式子表示）；(2)、为达到每月销售这种工艺品的利润为元，且要求降价不超过元，那么每件工艺品应降价多少元？22. 如图 1，在等腰直角三角形 ABC中，AB=AC，∠BAC=90°，点 D在 BC 边上，连接AD，AE⊥AD，AE=AD，连接 CE，DE.
(1)、求证：∠B=∠ACE.(2)、如图2，点A关于直线CE的对称点为M，连接CM，EM.①求证：∠CME=∠BAD；
②当 D，E，M三点共线时，∠BAD的度数为_▲_
五、解答题（三）（本大题 2小题，每小题12分，共24分）
-
23. 如图 1，⊙O为△ABC 的外接圆，AC=BC，D为OC与AB的交点，E为线段OC延长线上一点，且∠EAC=∠ABC.
图1 图2
(1)、求证：直线AE是⊙O的切线.(2)、若CD=5，AB=24，求⊙O的半径；(3)、如图 2，在（2）的基础上，点F在⊙O上，且 ， 点G是△ACF的内心，连接CG，请补全图形，并求CG 的长.24. 如图，抛物线y=﹣x2+bx +c与x轴交于A（4，0），B（﹣1，0）两点，与y轴交于点C，点D是抛物线上一动点，点E是线段AC的中点，连接AD，以AE和AD为一组邻边作口ADGE.
(1)、求b，c的值；(2)、当点D在直线 AC 上方的抛物线上时，求口ADGE面积的最大值及此时点D的坐标；(3)、当点G落在坐标轴上时，请直接写出点D的坐标.