广东省清远市清城区 2024年中考数学二模试卷
试卷更新日期:2024-03-04 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1. 在下列各数中,是无理数的是( )A、﹣1 B、 C、3.14 D、2. 是第五代移动通信技术,网络理论下载速度可以达到每秒以上,用科学记数法表示是( )A、 B、 C、 D、3. 如图,直线AB∥CD , AD平分∠BDC , ∠1=70°,那么∠2的度数是( )
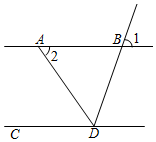 A、70° B、65° C、60° D、55°4. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,请找出以下四个图形中不是从正面、左面、上面看到的( )
A、70° B、65° C、60° D、55°4. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,请找出以下四个图形中不是从正面、左面、上面看到的( ) A、
A、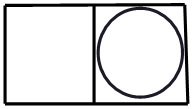 B、
B、 C、
C、 D、
D、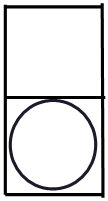 5. 点A(﹣1,4)关于原点对称的点的坐标为( )A、(1,4) B、(﹣1,﹣4) C、(1,﹣4) D、(4,﹣1)6. 下列运算正确的是( )A、(﹣a2b3)2=a4b6 B、a3•a5=a15 C、(﹣a2)3=﹣a5 D、3a2﹣2a2=17. 下列说法正确的是( )A、“任意画一个六边形,它的内角和是720度”,这是一个随机事件 B、为了解全国中学生的心理健康情况,应该采用全面调查的方式 C、一组数据6,8,7,9,7,10的众数和中位数都是7 D、若甲组数据的方差S甲2=0.4,乙组数据的方差S乙2=0.05,则乙组数据更稳定8. 小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )A、50≤x≤80 B、50≤x<80 C、50<x<80 D、50<x≤809. 如图,在Rt△ABC中,∠A=90°,BC= . 以BC的中点O为圆心的圆分别与AB , AC相切于D , E两点,则弧DE的长为( )
5. 点A(﹣1,4)关于原点对称的点的坐标为( )A、(1,4) B、(﹣1,﹣4) C、(1,﹣4) D、(4,﹣1)6. 下列运算正确的是( )A、(﹣a2b3)2=a4b6 B、a3•a5=a15 C、(﹣a2)3=﹣a5 D、3a2﹣2a2=17. 下列说法正确的是( )A、“任意画一个六边形,它的内角和是720度”,这是一个随机事件 B、为了解全国中学生的心理健康情况,应该采用全面调查的方式 C、一组数据6,8,7,9,7,10的众数和中位数都是7 D、若甲组数据的方差S甲2=0.4,乙组数据的方差S乙2=0.05,则乙组数据更稳定8. 小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )A、50≤x≤80 B、50≤x<80 C、50<x<80 D、50<x≤809. 如图,在Rt△ABC中,∠A=90°,BC= . 以BC的中点O为圆心的圆分别与AB , AC相切于D , E两点,则弧DE的长为( )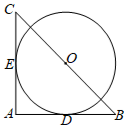 A、 B、 C、 D、π10. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )A、 B、 C、 或 D、 或
A、 B、 C、 D、π10. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )A、 B、 C、 或 D、 或二、填空题(共5小题,满分15分,每小题3分)
-
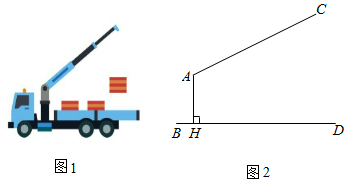
11. 分解因式:mn﹣m2= .12. 如果两个相似三角形对应边的比为2:3,那么它们对应高线的比是 .13. 方程1﹣3x=0的解是 .14. 图①是一辆吊车的实物图,图②是其工作示意图,AC是可以伸缩的起重臂,共转动点A离地面BD的高度AH为3.4m . 当AC=9m , ∠HAC=118°时,则操作平台C离地面的高度为 m . (结果精确到0.1米)【参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53】
 15. 如图,已知等边三角形ABC的边长为 , 点D为平面内一动点,且DA=1,将点D绕点C按逆时针方向转转60°,得到点E , 连接AE , 则AE的最大值是 .
15. 如图,已知等边三角形ABC的边长为 , 点D为平面内一动点,且DA=1,将点D绕点C按逆时针方向转转60°,得到点E , 连接AE , 则AE的最大值是 .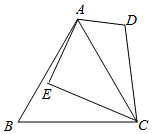
三、解答题(共8小题,满分75分)
-
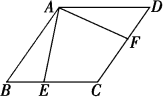
16. 计算: .17. 如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
 18. (x+2)2+(2x+1)(2x﹣1)﹣4x(x+1),其中x=..19. 为了使二十大精神深入人心,某地区举行了学习宣传贯彻党的二十大精神答题竞赛,试卷题目共10题,每题10分.现分别从三个小区中各随机取10名群众的成绩(单位:分),收集数据如下:
18. (x+2)2+(2x+1)(2x﹣1)﹣4x(x+1),其中x=..19. 为了使二十大精神深入人心,某地区举行了学习宣传贯彻党的二十大精神答题竞赛,试卷题目共10题,每题10分.现分别从三个小区中各随机取10名群众的成绩(单位:分),收集数据如下:锦绣城:90,70,80,70,80,80,80,90,80,100;
万和城:70,70,80,80,60,90,90,90,100,90;
龙泽湾:90,60,70,80,70,80,80,90,100,100.
整理数据:
分数
人数
小区
60
70
80
90
100
锦绣城
0
2
a
2
1
万和城
1
2
2
14
1
龙泽湾
1
2
3
2
2
分析数据:
平均数
中位数
众数
锦绣城
82
80
80
万和城
82
b
90
龙泽湾
82
80
c
根据以上信息回答下列问题:
(1)、请直接写出表格中a , b , c的值;(2)、比较这三组样本数据的平均数,中位数和众数,你认为哪个小区的成绩比较好?请说明理由;(3)、为了更好地学习宣传贯彻党的二十大精神,该地区将给竞赛成绩满分的群众颁发奖品,统计该地区参赛的选手数为3000人,试估计需要准备多少份奖品?20. 如图,在⊙O中,AB是直径,∠ABC=40°,点P在优弧BAC上.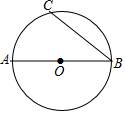 (1)、利用尺规作图,作CD∥AB , 交⊙O于点D . (不写作法,但要求保留作图痕迹).(2)、在(1)中,连接CP , DP , CO , DO , 求∠CPD的度数.21. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A , B类摊位占地面积各为多少平方米?(2)、该社区拟建A , B两类摊位共90个,且B类摊位的数量不大于A类摊位数量的3倍,建造这90个摊位的总费用不超过10850元.则共有哪几种建造方案?(3)、在(2)的条件下,哪种方案的总费用最少?最少费用是多少?22. 已知一次函数y=kx+b与反比例函数y=(mk≠0)的图象相交于点A(1,6)和点B(n , ﹣2).
(1)、利用尺规作图,作CD∥AB , 交⊙O于点D . (不写作法,但要求保留作图痕迹).(2)、在(1)中,连接CP , DP , CO , DO , 求∠CPD的度数.21. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A , B类摊位占地面积各为多少平方米?(2)、该社区拟建A , B两类摊位共90个,且B类摊位的数量不大于A类摊位数量的3倍,建造这90个摊位的总费用不超过10850元.则共有哪几种建造方案?(3)、在(2)的条件下,哪种方案的总费用最少?最少费用是多少?22. 已知一次函数y=kx+b与反比例函数y=(mk≠0)的图象相交于点A(1,6)和点B(n , ﹣2).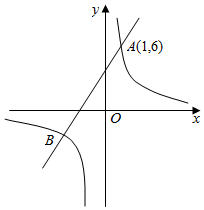 (1)、试确定一次函数与反比例函数的表达式;(2)、若点P在x轴上,且△PAB的面积为12,求点P的坐标;(3)、结合图象直接写出不等式kx+b>的解集.23. 已知四边形ABCD中,E , F分别是AB , AD边上的点,DE与CF交于点G , 令=k .
(1)、试确定一次函数与反比例函数的表达式;(2)、若点P在x轴上,且△PAB的面积为12,求点P的坐标;(3)、结合图象直接写出不等式kx+b>的解集.23. 已知四边形ABCD中,E , F分别是AB , AD边上的点,DE与CF交于点G , 令=k .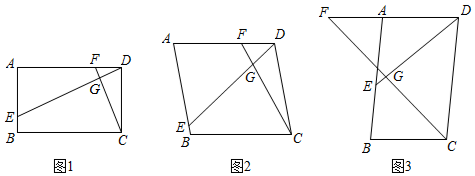 (1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.
(1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.