广东省深圳市2023年九年级上册期末考试数学模拟卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题(共10小题,满分30分,每小题3分)
-
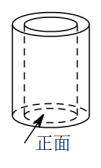
1. 如图是一个空心圆柱体,其主视图是( )
 A、
A、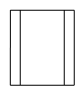 B、
B、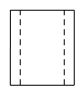 C、
C、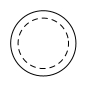 D、
D、 2. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、6个 B、15个 C、12个 D、13个3. 在直角△ABC中,∠C=90°,BC=3,sinA= , 求tanB为( )A、 B、 C、 D、4. 如图,已知直线l1∥l2∥l3 , 直线AC分别与直线l1、l2、l3交于A、B、C三点,直线DF分别与直线l1、l2、l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1,则OF的长是( )
2. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、6个 B、15个 C、12个 D、13个3. 在直角△ABC中,∠C=90°,BC=3,sinA= , 求tanB为( )A、 B、 C、 D、4. 如图,已知直线l1∥l2∥l3 , 直线AC分别与直线l1、l2、l3交于A、B、C三点,直线DF分别与直线l1、l2、l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1,则OF的长是( ) A、1 B、2 C、3 D、45. 若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )A、k<1 B、k≤1 C、k<1且k≠0 D、k≤1且k≠06. 已知反比例函数 , 点A(x1 , y1),B(x2 , y2)都在其图象上,下列说法不正确的是( )A、图象分布在第二、四象限 B、当x<0时,y随x的增大而增大 C、图象经过点(3,﹣1) D、若x1<x2 , 则 y1<y27. 要组织一次排球邀请赛,参赛的每两个队都要比赛一场(单循环比赛).根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,则比赛组织者应邀请( )个队参赛.A、6 B、7 C、8 D、98. 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,=3,则△ABC的面积为( )
A、1 B、2 C、3 D、45. 若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )A、k<1 B、k≤1 C、k<1且k≠0 D、k≤1且k≠06. 已知反比例函数 , 点A(x1 , y1),B(x2 , y2)都在其图象上,下列说法不正确的是( )A、图象分布在第二、四象限 B、当x<0时,y随x的增大而增大 C、图象经过点(3,﹣1) D、若x1<x2 , 则 y1<y27. 要组织一次排球邀请赛,参赛的每两个队都要比赛一场(单循环比赛).根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,则比赛组织者应邀请( )个队参赛.A、6 B、7 C、8 D、98. 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,=3,则△ABC的面积为( ) A、15 B、12 C、9 D、69. 如图,把一根4.5米长的竹竿斜靠在石坝旁,量出竿长1米时它离地面的高度是0.6米,又量得竿顶与坝脚的距离BC=2.8米,∠CBF记作α , 下列式子正确的是( )
A、15 B、12 C、9 D、69. 如图,把一根4.5米长的竹竿斜靠在石坝旁,量出竿长1米时它离地面的高度是0.6米,又量得竿顶与坝脚的距离BC=2.8米,∠CBF记作α , 下列式子正确的是( ) A、sinα= B、cosα= C、sinα= D、tanα=10. 如图,正方形ABCD中,E为BC中点连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④ ,其中结论正确的个数有( )
A、sinα= B、cosα= C、sinα= D、tanα=10. 如图,正方形ABCD中,E为BC中点连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④ ,其中结论正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(共5小题,满分15分,每小题3分)
-
11. 若 ,则 .12. 若关于x的一元二次方程x2﹣mx﹣6=0的一个根是x=3,则m的值为 .13. 如图,在菱形ABCD中,对角线AC=8,BD=6,则菱形的面积是 .
 14. 如图,在正方形网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点O,则∠AOC的正弦值是 .
14. 如图,在正方形网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点O,则∠AOC的正弦值是 . 15. 如图,直线y=mx﹣1交y轴于点B,交x轴于点C,以BC为边的正方形ABCD的顶点A(﹣1,a)在双曲线y=﹣(x<0)上,D点在双曲线y=(x>0)上,则k的值为 .
15. 如图,直线y=mx﹣1交y轴于点B,交x轴于点C,以BC为边的正方形ABCD的顶点A(﹣1,a)在双曲线y=﹣(x<0)上,D点在双曲线y=(x>0)上,则k的值为 .
三、解答题(共7小题,满分55分)
-
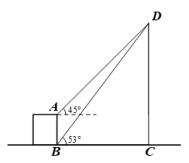
16. 解方程:x(x+2)=3x+6.17. 某医院计划选派护士支援某地的防疫工作,甲、乙、丙、丁4名护士积极报名参加,其中甲是共青团员,其余3人均是共产党员.医院决定用随机抽取的方式确定人选.(1)、随机抽取1人,甲恰好被抽中的概率是;(2)、若需从这4名护士中随机抽取2人,请用画树状图法或列表法求出被抽到的两名护士都是共产党员的概率.18. 如图,从楼层底部 处测得旗杆 的顶端 处的仰角是 ,从楼层顶部 处测得旗杆 的顶端 处的仰角是 ,已知楼层 的楼高为 米.求旗杆 的高度约为多少米?(参考数据: )
 19. 如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
19. 如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG. (1)、求证:四边形CEFG是菱形;(2)、若AB=6,AD=10,求四边形CEFG的面积.20. 由于新冠疫情的影响,口罩需求量急剧上升,经过连续两次价格的上调,口罩的价格由每包10元涨到了每包14.4元,(1)、求出这两次价格上调的平均增长率;(2)、在有关部门调控下,口罩价格还是降到了每包10元,而且调查发现,定价为每包10元时,一天可以卖出30包,每降价1元,可以多卖出5包,当销售额为315元时,且让顾客获得更大的优惠,应该降价多少元?21.
(1)、求证:四边形CEFG是菱形;(2)、若AB=6,AD=10,求四边形CEFG的面积.20. 由于新冠疫情的影响,口罩需求量急剧上升,经过连续两次价格的上调,口罩的价格由每包10元涨到了每包14.4元,(1)、求出这两次价格上调的平均增长率;(2)、在有关部门调控下,口罩价格还是降到了每包10元,而且调查发现,定价为每包10元时,一天可以卖出30包,每降价1元,可以多卖出5包,当销售额为315元时,且让顾客获得更大的优惠,应该降价多少元?21. (1)、【模型发现】如图1,△ABC∽△ADE,求证:△ABD∽△ACE.(2)、【深入探究】如图2,等边△ABC中,AB=3,D是AC上的动点,连接BD,将BD绕着点D逆时针旋转60°得到DE,连接CE,当点D从A运动到C时,求点E的运动路径长.(3)、【应用拓展】如图3,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,E是AD上的一点,连接BE,将BE绕着点E逆时针旋转90°,得到EF,EF交BC于点G,连接CF,若EG=FG,则的值为 .22. 如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数y=(k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(4,3).
(1)、【模型发现】如图1,△ABC∽△ADE,求证:△ABD∽△ACE.(2)、【深入探究】如图2,等边△ABC中,AB=3,D是AC上的动点,连接BD,将BD绕着点D逆时针旋转60°得到DE,连接CE,当点D从A运动到C时,求点E的运动路径长.(3)、【应用拓展】如图3,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,E是AD上的一点,连接BE,将BE绕着点E逆时针旋转90°,得到EF,EF交BC于点G,连接CF,若EG=FG,则的值为 .22. 如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数y=(k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(4,3). (1)、当点D恰好是FG中点时,求此时点C的横坐标;(2)、如图2,连接EF,求证:CD∥EF;(3)、如图3,将△CGD沿CD折叠,点G恰好落在边OB上的点H处,求此时反比例函数的解析式.
(1)、当点D恰好是FG中点时,求此时点C的横坐标;(2)、如图2,连接EF,求证:CD∥EF;(3)、如图3,将△CGD沿CD折叠,点G恰好落在边OB上的点H处,求此时反比例函数的解析式.