广东省深圳市2023-2024学年九年级数学适应性模拟考试试卷

试卷更新日期：2024-03-04 类型：中考模拟

进入出卷网下载

一、单选题（共30分）

1. 下列方程是一元二次方程的是（）

A、x²﹣5x＝1 B、3x+2y＝1 C、x²﹣ $\frac{1}{x}$ ＝1 D、ax²﹣3x+1＝0

查看试题解析
2. 关于 $x$ 的一元二次方程 $(m - 1) x^{2} + 2 x - m^{2} + 1 = 0$ ，常数项为 $0$ ，则 $m$ 值等于（）

A、 $1$ B、 $- 1$ C、 $\pm 1$ D、无法确定

查看试题解析
3. 如图是某几何体的三视图，这个几何体的侧面积是（）

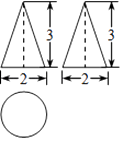A、6π B、2 $\sqrt{10}$ π C、 $\sqrt{10}$ π D、3π

查看试题解析
4. 目前电影《红船》票房已突破60亿元．第一天票房约3亿元，三天后票房累计总收入达9.5亿元，如果第二天，第三天票房收入按相同的增长率增长，增长率设为x ．则可列方程为（）

A、 $3 (1 + x) = 9.5$ B、 $3 {(1 + x)}^{2} = 9.5$ C、 $3 + 3 {(1 + x)}^{2} = 9.5$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 9.5$

查看试题解析
5. 如图，已知：在梯形ABCD中，CD∥AB，AD、BC的延长线相交于点E，AC、BD相交于点O，连接EO并延长交AB于点M，交CD于点N．则S_△_AOE：S_△_BOE等于（）

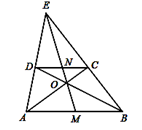A、1∶1 B、4∶3 C、3∶4 D、3∶2

查看试题解析
6. 如图，A、B是反比例函数 $y = \frac{2}{x}$ 的图象上关于原点O对称的任意两点，过点A作AC⊥x轴于点C，连接BC，则△ABC的面积为（）．

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，有一高度为8m的灯塔AB ，在灯光下，身高为1.6m的小亮从距离灯塔底端4.8m的点C处，沿BC方向前进3.2m到达点D处，那么他的影长（）

A、变长了0.8m B、变长了1.2m C、变短了0.8m D、变短了1.2m

查看试题解析
8. 如图，在 $△ A B C$ 中， $D$ ， $E$ 分别是 $B C$ ， $A C$ 的中点， $A D$ 和 $B E$ 相交于点 $G$ ，若 $A D = 6$ ，则 $A G$ 的长度为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 如图，正方形ABCD的对角线相交于O点，BE平分∠ABO交AO于E点，CF⊥BE于F点，交BO于G点，连接EG、OF，下列四个结论：①CE=CB；②AE= $\sqrt{2}$ OE；③OF= $\frac{1}{2}$ CG，其中正确的结论只有（）

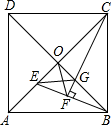A、①②③ B、②③ C、①③ D、①②

查看试题解析
10. 如图，在正方形 $A B C D$ 中，AB=6，E为AD的中点， $P$ 为对角线 $B D$ 上的一个动点，则 $A P + E P$ 最小值的是（）

A、6 B、 $4 \sqrt{3}$ C、 $3 \sqrt{5}$ D、 $6 \sqrt{2}$

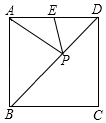查看试题解析

二、填空题(15分)

11. 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．若AB=8，AD=6 $\sqrt{3}$ ，AF=4 $\sqrt{3}$ ，则AE的长为．

查看试题解析
12. 在一个四宫格火锅里有三种锅底，一种是清汤锅底，一种是麻辣锅底．一种是红汤锅底，服务员将100粒丸子随机投入四个宫格中，就餐的小伙伴数了数，结果有49粒是清汤味的，估计倒入红汤锅底的丸子数是．

查看试题解析
13. 如图，正方形EFGH的四个顶点分别在正方形ABCD的四条边上，若正方形EFGH与正方形ABCD的相似比为 $\frac{\sqrt{5}}{3}$ ，则 $\frac{A E}{B E}$ （ $A E < B E$ ）的值为.

查看试题解析
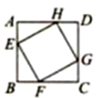14. 如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为．

查看试题解析
15. 如图，长方形 $A B C D$ 中， $A B = 8 c m$ ， $B C = 6 c m$ ， $Q$ 为 $C D$ 的中点．动点 $P$ 从 $A$ 点出发，以每秒 $2 c m$ 的速度沿 $A - B - C - Q$ 运动，最终到达点 $Q$ ，若点 $P$ 运动的时间为 $x$ 秒，则当 $x =$ 时， $△ A P Q$ 的面积等于 $20 c m^{2}$ ．

查看试题解析

三、解答题

16. 解方程：

(1)、 ${(2 x - 1)}^{2} = - 3 (2 x - 1)$

(2)、 $2 x^{2} - x - 3 = 0$ （用配方法）

查看试题解析
17. 木盒内有四个形状、大小完全相同的小球，分别标注数字 $1$ 、 $2$ 、 $3$ 、 $4$ ．

(1)、从木盒内随机摸取一个小球，球上标注的数字是偶数的概率是；

(2)、从木盒内连续摸出两个小球组成一个两位数（摸出后不放回），将第一次摸出的数作为十位数字，将第二次摸出的数作为个位数字，请用树状图或列表法求出这个两位数是3的倍数的概率．

查看试题解析
18. 如图，已知△ABC中，D是BC边上一点，过点D分别作DE∥AC交AB于点E ，作DF∥AB交AC于点F ，连接AD ．

(1)、下列条件：
①D是BC边的中点；②AD是△ABC的角平分线；③点E与点F关于直线AD对称．
请从中选择一个能证明四边形AEDF是菱形的条件，并写出证明过程；

(2)、若四边形AEDF是菱形，且AE＝4，CF＝2，求BE的长．

查看试题解析
19. 随着疫情防控全面放开，“复工复产”成为主旋律．中航无人机公司统计发现：公司今年2月份生产A型无人机2000架，4月份生产A型无人机达到12500架．

(1)、求该公司生产 $A$ 型无人机每月产量的平均增长率；

(2)、该公司还生产 $B$ 型无人机，已知生产1架A型无人机的成本200元，生产1架 $B$ 型无人机的成本是300元．若生产 $A 、 B$ 两种型号无人机共100架，预算投入生产的成本不高于22500元，问最多能生产 $B$ 型无人机多少架？

查看试题解析
20. 在Rt△ABC中，∠C=90°，AB=10，AC=8，点Q在AB上，且AQ=2，过Q作QR⊥AB ，垂足为Q ， QR交折线AC﹣CB于R（如图1），当点Q以每秒2个单位向终点B移动时，点P同时从A出发，以每秒6个单位的速度沿AB﹣BC﹣CA移动，设移动时间为t秒（如图2）．

(1)、求△BCQ的面积S与t的函数关系式．

(2)、t为何值时，QP∥AC？

(3)、t为何值时，直线QR经过点P？

(4)、当点P在AB上运动时，以PQ为边在AB上方所作的正方形PQMN在Rt△ABC内部，求此时t的取值范围．

查看试题解析
21. 图形的旋转变换是研究数学相关问题的重要手段之一．小华和小芳对等腰直角三角形的旋转变换进行研究．如图（1），已知 $△ A B C$ 和△ADE均为等腰直角三角形，点D ， E分别在线段 $A B ， A C$ 上，且 $∠ C = ∠ A E D = 90 °$ ．

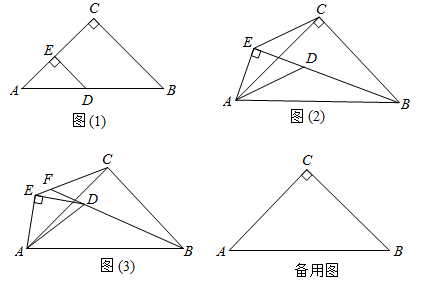(1)、观察猜想
小华将△ADE绕点A逆时针旋转，连接 $B D ， C E$ ，如图（2），当 $B D$ 的延长线恰好经过点E时，
① $\frac{B D}{C E}$ 的值为；
② $∠ B E C$ 的度数为度；

(2)、类比探究
如图（3），小芳在小华的基础上，继续旋转△ADE，连接 $B D ， C E$ ，设 $B D$ 的延长线交 $C E$ 于点F ，请求出 $\frac{B D}{C E}$ 的值及 $∠ B F C$ 的度数，并说明理由．

(3)、拓展延伸
若 $A E = D E = \sqrt{2} ， A C = B C = \sqrt{10}$ ，当 $C E$ 所在的直线垂直于 $A D$ 时，请你直接写出 $B D$ 的长．

查看试题解析