广东省深圳市龙岗区2023-2024学年九年级上学期数学期末试卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
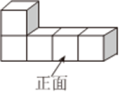
1. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、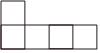 C、
C、 D、
D、 2. 如图,一个可以自由转动的转盘,被分成了白色和红色两个区域,任意转动转盘一次,当转盘停止转动时(若指针停在边界处,则重新转动转盘),指针落在红色区域内的概率是( )
2. 如图,一个可以自由转动的转盘,被分成了白色和红色两个区域,任意转动转盘一次,当转盘停止转动时(若指针停在边界处,则重新转动转盘),指针落在红色区域内的概率是( )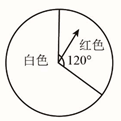 A、 B、 C、 D、3. 如图,在梯形中,交于点 , 已知 , , , , 则梯形的面积为( )
A、 B、 C、 D、3. 如图,在梯形中,交于点 , 已知 , , , , 则梯形的面积为( )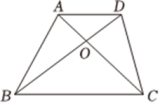 A、 B、 C、 D、4. 已知点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 已知关于的一元二次方程 , 则( )A、 B、或 C、或 D、6. 下列选项中,不能被边长为的正方形及其内部所覆盖的图形是( )A、长度为的线段 B、边长为的等边三角形 C、斜边为的直角三角形 D、面积为的菱形7. 有大小、形状、颜色完全相同的3个乒乓球,每个球上分别标有数字1,2,3中的一个,将这3个球放入不透明的袋中搅匀,如果不放回的从中随机连续抽取两个,则这两个球上的数字之和为偶数的概率是( )A、 B、 C、 D、8. 如图,已知与位似,且与的面积之比为: , 点的坐标为 , 则点的坐标为( )
A、 B、 C、 D、4. 已知点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 已知关于的一元二次方程 , 则( )A、 B、或 C、或 D、6. 下列选项中,不能被边长为的正方形及其内部所覆盖的图形是( )A、长度为的线段 B、边长为的等边三角形 C、斜边为的直角三角形 D、面积为的菱形7. 有大小、形状、颜色完全相同的3个乒乓球,每个球上分别标有数字1,2,3中的一个,将这3个球放入不透明的袋中搅匀,如果不放回的从中随机连续抽取两个,则这两个球上的数字之和为偶数的概率是( )A、 B、 C、 D、8. 如图,已知与位似,且与的面积之比为: , 点的坐标为 , 则点的坐标为( )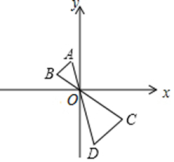 A、 B、 C、 D、9. 如图,▱ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=cm,则EF的长为( )
A、 B、 C、 D、9. 如图,▱ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=cm,则EF的长为( )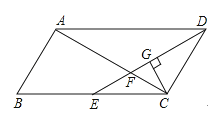 A、2cm B、cm C、1cm D、cm10. 如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处, , , 则的长为( )
A、2cm B、cm C、1cm D、cm10. 如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处, , , 则的长为( )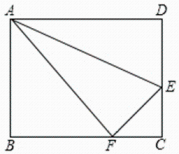 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共5小题,每小题3分,共15分。
-
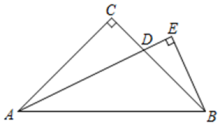
11. 已知关于x的一元二次方程有两个相等的实数根,则m的值为 .12. 设、是方程的两根,则 .13. 如图,是等腰直角三角形, , 为边上一点,连结 , 过点作 , 交的延长线于点若 , 则的值为 .
 14. 将长度为8厘米的木棍截成三段,每段长度均为整数厘米.如果截成的三段木棍长度分别相同算作同一种截法(如:5,2,1和1,5,2),那么截成的三段木棍能构成三角形的概率是 .15. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .
14. 将长度为8厘米的木棍截成三段,每段长度均为整数厘米.如果截成的三段木棍长度分别相同算作同一种截法(如:5,2,1和1,5,2),那么截成的三段木棍能构成三角形的概率是 .15. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .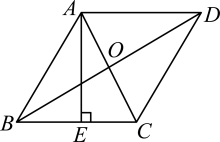
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
-
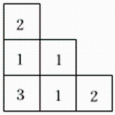
16. 若一个几何体由几个大小相同的小正方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.请画出从正面、左面看到的这个几何体的形状图.
 17. 已知关于的方程的一根为 .(1)、求的值;(2)、求方程的另一根.18. 如图,路灯点距地面米,小明在距路灯的底部点米的点时,测得此时他的影长为米.
17. 已知关于的方程的一根为 .(1)、求的值;(2)、求方程的另一根.18. 如图,路灯点距地面米,小明在距路灯的底部点米的点时,测得此时他的影长为米.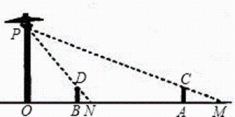 (1)、求小明的身高;(2)、小明沿所在的直线行走米到点时,身影的长度是变长了还是变短了?变长或变短了多少米?19. 商场以每件元的价格购进一批商品,以单价元销售.预计每月可售出件,该商场为尽可能减少库存,决定降价销售,根据市场调查,该商品单价每降低元,可多售出件,但最低售价应高于购进的价格;若该商场希望该商品每月获利元,则销售单价应定为多少元?每月可销售多少件?20. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球.(1)、请用画树形图或列表的方法写出两次取出的小球所能产生的全部结果;(2)、求两次取出的小球标号相同的概率;(3)、求两次取出的小球标号的和等于4的概率.21. 已知,如图,反比例函数的图象与一次函数的图象相交于点、 ,
(1)、求小明的身高;(2)、小明沿所在的直线行走米到点时,身影的长度是变长了还是变短了?变长或变短了多少米?19. 商场以每件元的价格购进一批商品,以单价元销售.预计每月可售出件,该商场为尽可能减少库存,决定降价销售,根据市场调查,该商品单价每降低元,可多售出件,但最低售价应高于购进的价格;若该商场希望该商品每月获利元,则销售单价应定为多少元?每月可销售多少件?20. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球.(1)、请用画树形图或列表的方法写出两次取出的小球所能产生的全部结果;(2)、求两次取出的小球标号相同的概率;(3)、求两次取出的小球标号的和等于4的概率.21. 已知,如图,反比例函数的图象与一次函数的图象相交于点、 ,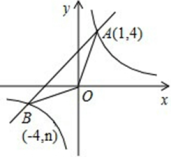 (1)、试确定这两个函数的表达式;(2)、求的面积;(3)、直接写出使反比例函数的值大于一次函数的值的的取值范围.22. 如图,在矩形ABCD中,AB=4cm,BC=11cm,点P从点D出发向终点A运动;同时点Q从点B出发向终点C运动.当P、Q两点其中有一点到达终点时,另一点随之停止,点P、Q的速度分别为1cm/s,2cm/s,连接PQ、AQ、CP.设点P、Q运动的时间为t(s).
(1)、试确定这两个函数的表达式;(2)、求的面积;(3)、直接写出使反比例函数的值大于一次函数的值的的取值范围.22. 如图,在矩形ABCD中,AB=4cm,BC=11cm,点P从点D出发向终点A运动;同时点Q从点B出发向终点C运动.当P、Q两点其中有一点到达终点时,另一点随之停止,点P、Q的速度分别为1cm/s,2cm/s,连接PQ、AQ、CP.设点P、Q运动的时间为t(s).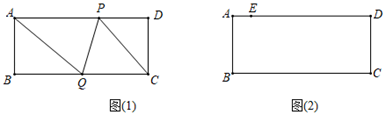 (1)、如图(1),当t为何值时,四边形ABQP是矩形?(2)、如图(2),若点E为边AD上一点,当AE=3cm时,四边形EQCP可能为菱形吗?若能,请求出t的值;若不能,请说明理由.
(1)、如图(1),当t为何值时,四边形ABQP是矩形?(2)、如图(2),若点E为边AD上一点,当AE=3cm时,四边形EQCP可能为菱形吗?若能,请求出t的值;若不能,请说明理由.