广东省佛山市顺德区2023-2024学年九年级上学期数学期末试卷

试卷更新日期：2024-03-04 类型：期末考试

进入出卷网下载

一、选择题（共10小题，每小题3分）

1. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一，具有极高的历史价值、文化价值．如图所示，关于它的三视图，下列说法正确的是（）

A、主视图与左视图相同 B、主视图与俯视图相同 C、左视图与俯视图相同 D、三种视图都相同

查看试题解析
2. 下列说法正确的是（　　）

A、四边相等的四边形是正方形 B、对角线互相垂直且相等的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分的四边形是菱形

查看试题解析
3. 已知菱形的边长为13cm ，它的一条对角线长为10cm ，则该菱形的面积为（　　）

A、60cm² B、120cm² C、240cm² D、480cm²

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 2 x - 5 = 0$ 时，将它化为 $(x + a)^{2} = b$ 的形式，则 $2 a + b$ 的值为（）

A、4 B、5 C、6 D、7

查看试题解析
5. 从1、2、3这三个数中任取两个不同的数，分别记为 $m 、 n$ ，那么点 $(m ， n)$ 在反比例函数 $y = \frac{6}{x}$ 的图象上的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{4}{9}$ D、 $\frac{2}{9}$

查看试题解析
6. 如图，在边长为1的小正方形组成的网格中，A，B，C，D四个点均在格点上， $A C$ 与 $B D$ 相交于点E，连接 $A B ， C D$ ，则 $△ A B E$ 与 $△ C D E$ 的周长比为（）

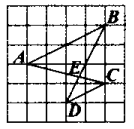A、1：4 B、4：1 C、1：2 D、2：1

查看试题解析
7. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变.如图，改变正方形ABCD的内角，正方形ABCD变为菱形 $A B C^{'} D^{'}$ ，若 $∠ D^{'} A B = 30^{°}$ ，则菱形 $A B C^{'} D^{'}$ 的面积与正方形ABCD的面积之比是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
8. 下列命题正确的是（）

A、已知：线段 $a = 1 c m ， b = 2 c m ， c = 3 c m ， d = 4 c m$ ，则 $a ， b ， c ， d$ 是比例线段 B、关于 $x$ 的方程 $(m^{2} + 1) x^{2} - 3 = 0$ 是一元二次方程 C、已知点 $A (- 1 ， y_{1}) ， B (- 2 ， y_{2})$ 是函数 $y = - \frac{5}{x}$ 图象上的两点，则 $y_{2} > y_{1}$ D、角都对应相等的两个多边形是相似多边形，边都对应成比例的多边形也是相似多边形

查看试题解析
9. 如图1，已知A，B是反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）图象上的两点， $B C ∥ x$ 轴，交y轴于点C，动点P从坐标原点O出发，沿 $O \to A \to B \to C$ （图中“ $\to$ ”所示路线）匀速运动，终点为C，过P作 $P M ⊥ x$ 轴，垂足为M.设三角形 $O M P$ 的面积为S，P点运动时间为t，则S关于t的函数图象大致如图2，则k的值为（）

A、8 B、6 C、4 D、2

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $A B = 6 ， B C = 9$ ，点 $E 、 F$ 分别在边 $A B 、 B C$ 上， $A E = 2 ， B D 、 E F$ 交于点 $G$ ，若 $G$ 是 $E F$ 的中点，则 $B F$ 的长是（）

A、5 B、6 C、6.4 D、7.2

查看试题解析

二、填空题（共5小题，每小题4分）

11. 若3n＝4m（mn≠0），则 $\frac{n}{m}$ ＝．

查看试题解析
12. 在一个不透明的袋子中装有红、白两种颜色的小球共20个，这些小球除了颜色不同外其它特质均相同．欣欣同学进行了摸球试验，每次摸出一个小球记下颜色，然后放回袋中搅拌均匀，再从中摸出一个…如此重复，经大量的试验发现摸到红球的频率稳定在0.60左右，由此可以估计袋中红球的个数为个．

查看试题解析
13. 在一元二次方程 $a x^{2} + b x + c = 0$ 中，若 $a 、 b 、 c$ 满足关系式 $4 a - 2 b + c = 0$ ，则这个方程必有一个根为．

查看试题解析
14. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6$ ， $B C = 8$ ，D是AB的中点，E是BC的中点， $E F ⊥ C D$ 于点F，则 $E F$ 的长是.

查看试题解析
15. 已知 $2 x^{2} - 3 x - 2 = 0$ ．则 $x^{2} + \frac{1}{x^{2}} =$ ．

查看试题解析

三、解答题（共6小题，共70分）

16. 用适当的方法解下列方程：

(1)、 $x (x - 5) = 3 x - 15$ ；

(2)、 $2 y^{2} - 9 y + 5 = 0$ ．

查看试题解析
17.

(1)、如图，在平面直角坐标系 $x O y$ 中，菱形 $O A B C$ 的顶点 $C$ 在 $x$ 轴的正半轴上．若点 $A$ 的坐标是 $(3 ， 4)$ ，求点 $B$ 的坐标．

(2)、关于 $x$ 的方程 $(a - 5) x^{2} - 4 x - 1 = 0$ 有实数根，求实数 $a$ 满足的条件．

查看试题解析
18. 【作图与探究】如图，在矩形 $A B C D$ 中， $A B = 6 ， B C = 8$ ．

(1)、用尺规作图法作菱形 $A E C F$ ，使点 $E 、 F$ 分别在 $B C$ 和 $A D$ 边上；

(2)、求 $E F$ 的长度．

查看试题解析
19. 某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图，是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度 $y (℃)$ 与时间 $x (h)$ 之间的函数关系，其中线段 $A B 、 B C$ 表示恒温系统开启阶段，双曲线的一部分 $C D$ 表示恒温系统关闭阶段．请根据图中信息解答下列问题：

(1)、求这天的温度 $y$ 与时间 $x (0 \leq x \leq 24)$ 的函数关系式；

(2)、求恒温系统设定的恒定温度；

(3)、若大棚内的温度低于 $10 ℃$ 时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？

查看试题解析
20. 问题情境：小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉，为了确定售价，小莹帮妈妈调查了附近A ， B ， C ， D ， E五家花卉店近期该种盆栽花卉的售价与日销售量情况，记录如下：

售价（元/盆）
日销售量（盆）
A
20
50
B
30
30
C
18
54
D
22
46
E
26
38
数据整理：（1）请将以上调查数据按照一定顺序重新整理，填写在下表中：
售价（元/盆）
____
____
____
____
____
日销售量（盆）
____
____
____
____
____

(1)、模型建立：分析数据的变化规律，找出日销售量与售价间的关系．

(2)、拓广应用：根据以上信息，小莹妈妈在销售该种花卉中，
①要想每天获得400元的利润，应如何定价？
②售价定为多少时，每天能够获得最大利润？

查看试题解析
21.
【综合与探究】问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知 $A D$ 是 $△ A B C$ 的角平分线，可证 $\frac{A B}{A C} = \frac{B D}{C D}$ ．小慧的证明思路是：如图2，过点 $C$ 作 $C E ∥ A B$ ，交 $A D$ 的延长线于点 $E$ ，构造相似三角形来证明 $\frac{A B}{A C} = \frac{B D}{C D}$ ．

(1)、尝试证明：请参照小慧提供的思路，利用图2证明： $\frac{A B}{A C} = \frac{B D}{C D}$ ；

(2)、应用拓展：如图3，在 $R t △ A B C$ 中， $∠ B A C = 90 ° ， D$ 是边 $B C$ 上一点．连接 $A D$ ，将 $△ A C D$ 沿 $A D$ 所在直线折叠，点 $C$ 恰好落在边 $A B$ 上的 $E$ 点处．
①若 $A C = 1 ， A B = 2$ ，求 $D E$ 的长；
②若 $B C = m ， ∠ A E D = α$ ，求 $D E$ 的长（用含 $m ， α$ 的式子表示）．

查看试题解析

	售价（元/盆）	日销售量（盆）
A	20	50
B	30	30
C	18	54
D	22	46
E	26	38

售价（元/盆）	____	____	____	____	____
日销售量（盆）	____	____	____	____	____