广东省深圳市南山区2023-2024学年八年级上学期数学期末试卷

试卷更新日期：2024-03-04 类型：期末考试

进入出卷网下载

一、选择题

1. 36的算术平方根是（）

A、 $\sqrt{6}$ B、6 C、 $\pm \sqrt{6}$ D、 $\pm 6$

查看试题解析
2. 在平面直角坐标系中，点 $(1 ， - 2)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 南山区博物馆五位小讲解员的年龄分别为10，12，12，13，15（单位：岁），则三年后这五位小讲解员的年龄数据中一定不会改变的是（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
4. 实数a ， b在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A、 $a > - 2$ B、 $a + b > 0$ C、 $| a | > | b |$ D、 $b - a < 0$

查看试题解析
5. 光在不同介质中的传播速度不同，当光从空气射向某透明液体时会发生折射．如图，在空气中平行的两条入射光线，其两条折射光线也是平行的，若水面和杯底互相平行，当 $∠ 1 = 50 °$ ， $∠ 2 = 115 °$ 时， $∠ 3 + ∠ 4 =$ （）

A、 $105 °$ B、 $115 °$ C、 $155 °$ D、 $165 °$

查看试题解析
6. 下列四个命题中，真命题是（）

A、若 $\sqrt{x - 3}$ 有意义，则 $x ≥ 3$ B、两个无理数的和还是无理数 C、体积为8的正方体，边长是无理数 D、两直线被第三条直线所截，内错角相等

查看试题解析
7. 《九章算术》是中国古代第一部数学专著，书中有这样一题：“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？”大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价格是多少？设共有 $x$ 个人，该物品价格是 $y$ 元，则下列方程组正确的是（）

A、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$ B、 ${\begin{array}{l} 8 y + 3 = x \\ 7 y - 4 = x \end{array}$ C、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ D、 ${\begin{array}{l} 8 y - 3 = x \\ 7 y + 4 = x \end{array}$

查看试题解析
8. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为 $∠ B A F$ 时，顶部边缘 $B$ 处离桌面的高度 $B C$ 为 $7 c m$ ，此时底部边缘 $A$ 处与 $C$ 处间的距离 $A C$ 为 $24 c m$ ，小组成员调整张角的大小继续探究，最后发现当张角为 $∠ D A F$ 时（ $D$ 是 $B$ 的对应点），顶部边缘 $D$ 处到桌面的距离 $D E$ 为 $20 c m$ ，则底部边缘 $A$ 处与 $E$ 之间的距离 $A E$ 为（）

A、 $\sqrt{69} c m$ B、 $10 \sqrt{5} c m$ C、 $21 c m$ D、 $15 c m$

查看试题解析
9. 如图，用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案，已知A（﹣2，6），则点B的坐标为（）

A、（﹣6，4） B、（ $- \frac{20}{3}$ ， $\frac{14}{3}$ ） C、（﹣6，5） D、（ $- \frac{20}{3}$ ， 4）

查看试题解析
10. 如图，这是一个供滑板爱好者使用的 $U$ 型池的示意图，该 $U$ 型池可以看作是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为 $8 m$ 的半圆，其边缘 $A B = C D = 20 m$ ，点 $E$ 在 $C D$ 上， $C E = 5 m$ ，一名滑板爱好者从 $A$ 点滑到 $E$ 点，则他滑行的最短距离为（）m（边缘部分的厚度可以忽略不计， $π$ 取3）

A、17 B、 $3 \sqrt{41}$ C、 $4 \sqrt{34}$ D、 $3 \sqrt{89}$

查看试题解析

二、填空题

11. 比较大小： $\sqrt{7}$ 3（填“ $<$ ”、“ $>$ ”或“ $=$ ”）．

查看试题解析
12. 一个正数的两个平方根分别是 $2 a - 1$ 与 $- a + 2$ ，则a的值为．

查看试题解析
13. 已知等腰 $△ A B C$ 的底边 $B C = 5$ ， D是腰 $A B$ 上一点，且 $C D = 4$ ， $B D = 3$ ，则 $A D$ 的长为.

查看试题解析
14. 如图1，11月10日晚，“深爱万物”—2023深圳人才嘉年华活动正式启动，千余架无人机在深圳人才公园上空上演“天空之舞”，为人才喝彩、向人才致敬．如图2的平面直角坐标系中，线段 $O A ， B C$ 分别表示1号、2号无人机在队形变换中飞行高度 $y_{1}$ ， $y_{2} (m)$ 与飞行时间 $x (s)$ 的函数关系，其中 $y_{2} = - 4 x + 150$ ，线段 $O A$ 与 $B C$ 相交于点P ， $A B ⊥ y$ 轴于点B ，点A的横坐标为25．则在第秒时1号和2号无人机在同一高度．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C = 6$ ， $B C = 10$ ，点 $D$ 是边 $B C$ 上一点（点 $D$ 不与点 $B$ ， $C$ 重合），将 $△ A B D$ 沿 $A D$ 翻折，点 $B$ 的对应点为点 $E$ ， $A E$ 交 $B C$ 于点 $F$ ，若 $D E ∥ A C$ ，则点 $C$ 到线段 $A D$ 的距离为．

查看试题解析

三、解答题

16. 计算：

(1)、 $(3 + \sqrt{5}) (\sqrt{5} - 2)$

(2)、 $\frac{\sqrt{12} + \sqrt{27}}{\sqrt{3}}$

查看试题解析
17. 已知实数x ， y满足 ${\begin{array}{l} 4 x - y = 3 \\ x + 6 y = 17 \end{array}$ ，求 $x + y$ 的值．

查看试题解析
18. 如图，在平面直角坐标系中， $△ A B C$ 各顶点分别为 $A (- 3 ， 3)$ ， $B (- 4 ， - 2)$ ， $C (- 1 ， - 1)$ ．

(1)、在图中作 $△ A^{'} B^{'} C^{'}$ ，使 $△ A^{'} B^{'} C^{'}$ 和 $△ A B C$ 关于y轴对称；

(2)、直接写出点B关于x轴对称的点的坐标；

(3)、在x轴上存在一点Q ，使得 $Q B + Q C$ 的值最小， $Q B + Q C$ 的最小值为；请直接写出点Q的坐标．

查看试题解析
19. 某校为丰富同学们的课余生活，全面提高科学素养，提升思维能力和科技能力，开展了“最强大脑”邀请赛，现从八年级（1）班和八年级（2）班各随机抽取了10名学生的初赛成绩（初赛成绩均为整数，满分为10分，9分及以上为优秀）统计、整理如下：八年级（1）班抽取的学生的初赛成绩：6，8，8，8，9，9，9，9，10，10．八年级（2）班抽取的学生的初赛成绩：6，7，8，8，8，9，10，10，10，10，请根据以上信息，完成下列问题：
八年级（1）班、八年级（2）班抽取的学生的初赛成绩统计表：
班级
平均数
中位数
众数
优秀率
八年级（1）班
8.6
9
b
m
八年级（2）班
8.6
a
10
$50 %$

(1)、填空： $a =$ ， $b =$ ， $m =$ ；

(2)、小明是抽取的20名学生中的一名，其成绩是9分．小明说：“在本班抽取的10名学生中，我的初赛成绩比一半同学的初赛成绩要好”，若小明的说法是正确的，则可判断小明是八年级班的学生（选填“（1）”或“（2）”）：

(3)、若八年级有学生500人，且满分才能进入决赛，估计八年级进入决赛的学生共有多少人？

查看试题解析
20. 南山区某社区为进一步落实全民健身政策，需要购买若干副羽毛球拍和乒乓球拍，用于社区球类比赛活动，已知购买2副羽毛球拍和1副乒乓球拍共需费用330元；购买5副羽毛球拍和2副乒乓球拍共需费用780元．

(1)、每副羽毛球拍和乒乓球拍的单价各是多少元？

(2)、根据社区实际情况，社区拟用810元购买若干副羽毛球拍和乒乓球拍，若810元恰好用完，且两种球拍均要购买，社区有哪几种购买方案？

查看试题解析
21. 【问题呈现】
如图①，已知线段 $A C$ ， $B D$ 相交于点 $O$ ，连结 $A B$ ， $C D$ ，我们把形如这样的图形称为“ $8$ 字型”．

(1)、证明： $∠ A + ∠ B = ∠ C + ∠ D$ ．

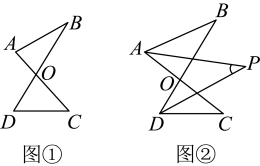(2)、【问题探究】
继续探究，如图②， $A P$ 、 $D P$ 分别平分 $∠ B A O$ 、 $∠ C D O$ ， $A P$ 、 $D P$ 交于点 $P$ ，求 $∠ P$ 与 $∠ B$ 、 $∠ C$ 之间的数量关系．为了研究这一问题，尝试代入 $∠ B$ 、 $∠ C$ 的值求 $∠ P$ 的值，得到下面几组对应值：
表中 $a =$ ，猜想得到 $∠ P$ 与 $∠ B$ 、 $∠ C$ 的数量关系为；

(3)、证明（ $2$ ）中猜想得到的 $∠ P$ 与 $∠ B$ 、 $∠ C$ 的数量关系；
$∠ B$ （单位：度）
$20$
$35$
$40$
$∠ C$ （单位：度）
$30$
$45$
$20$
$∠ P$ （单位：度）
$25$
$40$
$a$

查看试题解析
22. 先阅读下列材料，然后解决问题：
【阅读感悟】
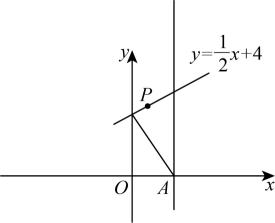
在平面直角坐标系中，已知点 $Q (t - 2 ， t + 3)$ ，当t的值发生改变时，点Q的位置也会发生改变，为了求点Q运动所形成的图象的解析式，令点Q的横坐标x ，纵坐标y ，得到了方程组 ${\begin{array}{l} t - 2 = x \\ t + 3 = y \end{array}$ 消去t ，得 $y - x = 5$ ，即 $y = x + 5$ ，可以发现，点 $Q$ 随t的变化而运动所形成的图象的解析式是 $y = x + 5$ ．

(1)、【尝试应用】
观察下列四个点的坐标，不在函数 $y = - x + 4$ 图象上的是____.

A、 $M (1 ， 3)$ B、 $N (t ， t - 4)$ C、 $P (4 - t ， t)$ D、 $P (2 t ， 4 - 2 t)$

(2)、求点 $M (3 - t ， 2 t - 7)$ 随t的变化而运动所形成的图象的解析式；

(3)、【综合运用】
如图，在平面直角坐标系中，点P在一次函数 $y = \frac{1}{2} x + 4$ 的图象上运动．已知点 $A (3 ， 0)$ 为定点，连接 $P A$ ，过点A作直线 $B A ⊥ P A$ ，且 $B A = P A$ ，求点B随点P的变化而运动所形成的图象的解析式．

查看试题解析

班级	平均数	中位数	众数	优秀率
八年级（1）班	8.6	9	b	m
八年级（2）班	8.6	a	10	$50 %$

$∠ B$ （单位：度）	$20$	$35$	$40$
$∠ C$ （单位：度）	$30$	$45$	$20$
$∠ P$ （单位：度）	$25$	$40$	$a$