广东省深圳市光明区2023-2024学年七年级上学期数学期末试卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一项是正确的)
-
1. 2024的倒数是( )A、 B、2024 C、 D、2. 深圳市地区生产总值统一核算结果显示,2023年光明区前3个季度地区生产总值为1113亿元,同比增长.数据1113亿用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的俯视图是( )
 A、
A、 B、
B、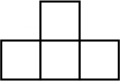 C、
C、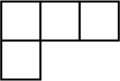 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 若是关于的方程的解,则的值是( )A、7 B、1 C、 D、-76. 根据“双减”要求,要充分保障学生睡眠的时间.光明区某学校为了解本校2000名学生的睡眠时间,从中抽查了200名学生的睡眠时间进行统计,下面叙述正确的是( )A、200名学生是总体的一个样本 B、总体是光明区某学校2000名学生 C、个体是学校每名学生的睡眠时间 D、以上说法都不正确7. ( )A、 B、 C、 D、8. 下列说法正确的是( )A、两点之间,直线最短 B、多项式的次数为3 C、六棱柱有8个面 D、“与的和的3倍”可表示为9. 某项工程由甲单独做需12天完成,由乙单独做需8天完成,若甲、乙共同做,则它们完成这项工程的时间是( )天.A、20 B、 C、12 D、810. 如图,第1个图形中有1个三角形,第2个图形中有5个三角形,第3个图形中有9个三角形,第10个图形中有( )个三角形.
4. 下列计算正确的是( )A、 B、 C、 D、5. 若是关于的方程的解,则的值是( )A、7 B、1 C、 D、-76. 根据“双减”要求,要充分保障学生睡眠的时间.光明区某学校为了解本校2000名学生的睡眠时间,从中抽查了200名学生的睡眠时间进行统计,下面叙述正确的是( )A、200名学生是总体的一个样本 B、总体是光明区某学校2000名学生 C、个体是学校每名学生的睡眠时间 D、以上说法都不正确7. ( )A、 B、 C、 D、8. 下列说法正确的是( )A、两点之间,直线最短 B、多项式的次数为3 C、六棱柱有8个面 D、“与的和的3倍”可表示为9. 某项工程由甲单独做需12天完成,由乙单独做需8天完成,若甲、乙共同做,则它们完成这项工程的时间是( )天.A、20 B、 C、12 D、810. 如图,第1个图形中有1个三角形,第2个图形中有5个三角形,第3个图形中有9个三角形,第10个图形中有( )个三角形.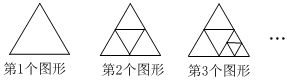 A、37 B、38 C、39 D、40
A、37 B、38 C、39 D、40二、填空题(本大题共5小题,每小题3分,共15分)
-
11. 如果与是同类项,那 .12. 扇形的圆心角为 , 半径为3,则这个扇形的面积为 . (结果保留)13. 已知 , 则.14. 如图,是的平分线, , , 则 , .
 15. 如图,点是线段上的两点(点在的左侧),点分别是线段和的中点,若 , 则线段的长为.
15. 如图,点是线段上的两点(点在的左侧),点分别是线段和的中点,若 , 则线段的长为.
三、解答题(本大题共7小题,共55分)
-
16. 计算:(1)、;(2)、.17. 先化简,再求值: , 其中 .18. 解方程: .19. 学习了频数分布直方图后,光明区某数学兴趣小组对某农场的西红柿大棚中每株西红柿秧结的小西红柿的个数做了调查.兴趣小组随机收集了这个农场西红柿大棚其中30株西红柿秧上结的小西红柿的个数如下:
28
62
54
39
32
47
68
27
65
43
52
59
67
59
45
42
79
51
54
25
82
18
39
32
64
74
49
37
39
52
(1)、数学兴趣小组采用的调查方式是;(填“普查”或“抽样调查”)(2)、将调查的30株西红柿秧上小西红柿的个数按组距为10将数据分组,列表如下:分组
频数
2
7
5
3
2
(16~26表示大于等于16同时小于26,其它分组中的“~”均表示这一含义)写出表中和的值;
(3)、根据以上的分组,画出频数分布直方图. 20. 足球是世界第一运动,2022年世界杯足球赛再一次点燃了人们对足球运动的热情.世界杯期间光明区某文具店用14400元购进了甲、乙两款足球,一共200个.两款足球的进价和标价如下表:
20. 足球是世界第一运动,2022年世界杯足球赛再一次点燃了人们对足球运动的热情.世界杯期间光明区某文具店用14400元购进了甲、乙两款足球,一共200个.两款足球的进价和标价如下表:类别
甲款足球
乙款足球
进价/(元/个)
80
60
标价/(元/个)
120
90
(1)、求该文具店的甲、乙两款足球分别购进多少个?(2)、该文具店为了加快销售,回笼资金,决定对甲款足球打8折销售,乙款足球打9折销售,若所购的足球全部售出,则该文具店能获利多少元?21. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”(如图1),“洛书”是一种关于天地空间变化脉络图案,它是以黑点与白点为基本要素,以一定方式构成若干不同组合.“洛书”用今天的数学符号翻译出来就是一个三阶幻方(如图2).三阶幻方又名九宫格,是一种将数字(1至9,数字不重复使用)安排在三行三列正方形格子中,使每行、列和对角线上的数字和都相等.
4
2
5
7
8
1
6
(1)、根据“洛书”中表达的意思,将图2中的三阶幻方补充完整;(2)、改变下表幻方中数字的位置,可以得到一个新的三阶幻方(如图3),请补全这个新的三阶幻方;2
7
9
1
3
8
(3)、如图4,有3个正方形,每个正方形的顶点处都有一个“ ”.将、、2、4、6、8、10、12这12个数填入恰当的位置(数字不重复使用),使每个正方形的4个顶点处“
”.将、、2、4、6、8、10、12这12个数填入恰当的位置(数字不重复使用),使每个正方形的4个顶点处“ ”中的数的和都为2.请直接写出的值.
”中的数的和都为2.请直接写出的值. 22. 小明同学喜欢玩折纸游戏,他发现折纸的过程中蕴含着丰富的数学知识,于是他用长方形纸片研究折纸过程中角的变化.他在长方形纸片的边上找到一点 , 边上找到一点 , 连接 , 沿着进行第一次折叠(如图1),使得点落在处,点落在处.
22. 小明同学喜欢玩折纸游戏,他发现折纸的过程中蕴含着丰富的数学知识,于是他用长方形纸片研究折纸过程中角的变化.他在长方形纸片的边上找到一点 , 边上找到一点 , 连接 , 沿着进行第一次折叠(如图1),使得点落在处,点落在处. (1)、若小明经过测量得到 , 则 .(2)、小明改变点和的位置重新折叠,第一次折叠后,将纸片沿着直线进行第二次折叠,使得点落在处(如图2,落在的左侧),若 , 求的大小.(请写出必要的推理过程)
(1)、若小明经过测量得到 , 则 .(2)、小明改变点和的位置重新折叠,第一次折叠后,将纸片沿着直线进行第二次折叠,使得点落在处(如图2,落在的左侧),若 , 求的大小.(请写出必要的推理过程) (3)、小明用一张新长方形纸片折成一架纸飞机,步骤如下图所示:
(3)、小明用一张新长方形纸片折成一架纸飞机,步骤如下图所示:
小明在步骤3时测得 , 在步骤5折叠机翼时,将机翼部分沿折痕折叠,使得 , 折痕交于点 , 此时满足 , 直接写出步骤6中的大小(左、右机翼展开后在同一平面上).