广西南宁重点中学2022-2023学年八年级(下)开学数学试卷
试卷更新日期:2024-03-04 类型:开学考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下面的图形是用数学家名字命名的,其中是轴对称图形的是( )A、
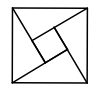 赵爽弦图
B、费马螺线
赵爽弦图
B、费马螺线  C、
C、 科克曲线
D、斐波那契螺旋线
科克曲线
D、斐波那契螺旋线  2. 下列式子中,是最简二次根式的是( )A、 B、 C、 D、3. 微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小某种电子元件的面积约为平方毫米,用科学记数法表示为( )A、 B、 C、 D、4. 内角和为的多边形是( )A、六边形 B、五边形 C、四边形 D、三边形5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,已知 , 那么添加下列一个条件后,仍无法判定≌的是( )
2. 下列式子中,是最简二次根式的是( )A、 B、 C、 D、3. 微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小某种电子元件的面积约为平方毫米,用科学记数法表示为( )A、 B、 C、 D、4. 内角和为的多边形是( )A、六边形 B、五边形 C、四边形 D、三边形5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,已知 , 那么添加下列一个条件后,仍无法判定≌的是( )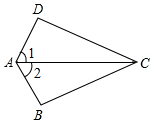 A、 B、 C、 D、7. 若分式的值为 , 则的值为( )A、或 B、 C、 D、8. 我区“人才引进”招聘考试分笔试和面试,按笔试占、面试占计算加权平均数作为总成绩应试者李老师的笔试成绩为分,面试成绩为分,则李老师的总成绩为( )A、 B、 C、 D、9. 如图,在数轴上点表示的数为 , 则的值为( )
A、 B、 C、 D、7. 若分式的值为 , 则的值为( )A、或 B、 C、 D、8. 我区“人才引进”招聘考试分笔试和面试,按笔试占、面试占计算加权平均数作为总成绩应试者李老师的笔试成绩为分,面试成绩为分,则李老师的总成绩为( )A、 B、 C、 D、9. 如图,在数轴上点表示的数为 , 则的值为( )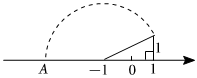 A、 B、 C、 D、10. 若关于的分式方程无解,则的值为( )A、 B、 C、或 D、11. 在如图所示的网格中,在格点上找一点 , 使为等腰三角形,则点有( )
A、 B、 C、 D、10. 若关于的分式方程无解,则的值为( )A、 B、 C、或 D、11. 在如图所示的网格中,在格点上找一点 , 使为等腰三角形,则点有( )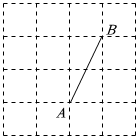 A、个 B、个 C、个 D、个12. 如图,已知直线:与轴的夹角是 , 过点作轴的垂线交直线于点 , 过点作直线的垂线交轴于点;过点作轴的垂线交直线于点 , 过点作直线的垂线交轴于点按此作法继续下去,则点的坐标为( )
A、个 B、个 C、个 D、个12. 如图,已知直线:与轴的夹角是 , 过点作轴的垂线交直线于点 , 过点作直线的垂线交轴于点;过点作轴的垂线交直线于点 , 过点作直线的垂线交轴于点按此作法继续下去,则点的坐标为( )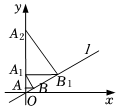 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
13. 二次根式 在实数范围内有意义,x的取值范围是.14. 分解因式: .15. 若关于的二次三项式是完全平方式,则的值为 .16. 如图,在中, , 平分 , 于点 , 若 , , 则的长为 .
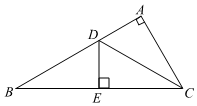 17. 如图,台阶阶梯每一层高 ,宽 ,长 .一只蚂蚁从 点爬到 点,最短路程是 .
17. 如图,台阶阶梯每一层高 ,宽 ,长 .一只蚂蚁从 点爬到 点,最短路程是 .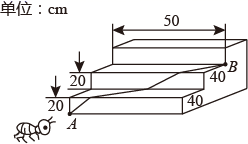 18. 如图,在 中, , ,以BC为边在BC的右侧作等边 ,点E为BD的中点,点P为CE上一动点,连结AP , BP . 当 的值最小时, 的度数为 .
18. 如图,在 中, , ,以BC为边在BC的右侧作等边 ,点E为BD的中点,点P为CE上一动点,连结AP , BP . 当 的值最小时, 的度数为 .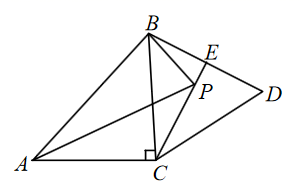
三、解答题:本题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤。
-
19. 计算:(1)、;(2)、20. 先化简,再求值: , 其中 .21. 如图,三个顶点的坐标分别为 , , .
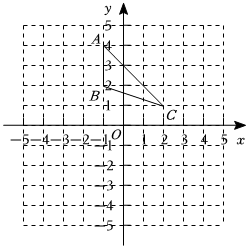 (1)、画出关于轴成轴对称的图形 , 并写出的坐标;(2)、作出的高 , 保留作图痕迹,不写作法,并直接写出的长.22. 如图,在四边形中, , , .
(1)、画出关于轴成轴对称的图形 , 并写出的坐标;(2)、作出的高 , 保留作图痕迹,不写作法,并直接写出的长.22. 如图,在四边形中, , , .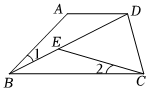 (1)、求证:≌;(2)、若 , , 求的度数.23. 数学源于生活,寓于生活,用于生活在人类历史发展和社会生活中,数学发挥着不可替代的作用为了激发学生学习数学的兴趣,某校计划购进什么是数学和古今数学思想若干套,已知元可购买什么是数学的数量比古今数学思想多套,且古今数学思想的单价是什么是数学单价的倍.(1)、求每套古今数学思想的价格;(2)、学校计划用不超过元购进这两套书共套,此时正赶上书城折销售所有书籍,求古今数学思想最多能买几套?24. 一艘轮船从港向南偏西方向航行到达岛,再从岛沿方向航行到达岛,港到航线的最短距离是 .
(1)、求证:≌;(2)、若 , , 求的度数.23. 数学源于生活,寓于生活,用于生活在人类历史发展和社会生活中,数学发挥着不可替代的作用为了激发学生学习数学的兴趣,某校计划购进什么是数学和古今数学思想若干套,已知元可购买什么是数学的数量比古今数学思想多套,且古今数学思想的单价是什么是数学单价的倍.(1)、求每套古今数学思想的价格;(2)、学校计划用不超过元购进这两套书共套,此时正赶上书城折销售所有书籍,求古今数学思想最多能买几套?24. 一艘轮船从港向南偏西方向航行到达岛,再从岛沿方向航行到达岛,港到航线的最短距离是 .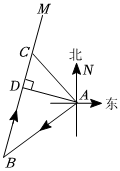 (1)、若轮船速度为小时,求轮船从岛沿返回港所需的时间.(2)、求岛在港的什么方向?25.
(1)、若轮船速度为小时,求轮船从岛沿返回港所需的时间.(2)、求岛在港的什么方向?25. (1)、【知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图 , 是用长为 , 宽为的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分小正方形的面积,可以得到、、三者之间的等量关系式: ;(2)、【知识迁移】如图所示的大正方体是由若干个小正方体和长方体拼成的,用两种不同的方法计算大正方体的体积,我们也可以得到一个等式: ;(3)、【成果运用】利用上面所得的结论解答:
(1)、【知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图 , 是用长为 , 宽为的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分小正方形的面积,可以得到、、三者之间的等量关系式: ;(2)、【知识迁移】如图所示的大正方体是由若干个小正方体和长方体拼成的,用两种不同的方法计算大正方体的体积,我们也可以得到一个等式: ;(3)、【成果运用】利用上面所得的结论解答:①已知 , , , 求的值;
②已知 , , 则 .
26. 如图,在平面直角坐标系中,已知点、分别为轴和轴上的点,且 , 满足 , 过点作于点 , 延长至点 , 使得 , 连接、 .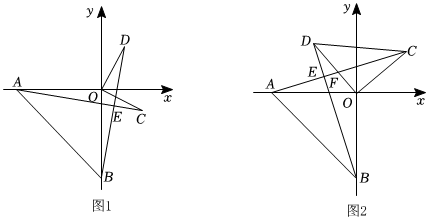 (1)、点的坐标为 ;的度数为 .(2)、如图 , 若点在第四象限,试判断与的数量关系与位置关系,并说明理由.(3)、如图 , 若点在第一象限,连接 , 平分 , 与交于点试判断与的数量关系,并说明理由.
(1)、点的坐标为 ;的度数为 .(2)、如图 , 若点在第四象限,试判断与的数量关系与位置关系,并说明理由.(3)、如图 , 若点在第一象限,连接 , 平分 , 与交于点试判断与的数量关系,并说明理由.