广东省深圳市福田区2023-2024学年重点中学八年级(上)期末数学试卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中.下列各组数中,是“勾股数”的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )
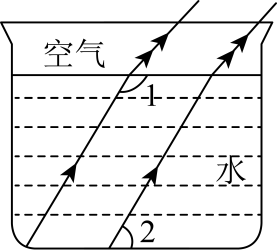 A、 B、 C、 D、4. 甲、乙两名射击运动员分别进行了相同次数的射击训练,如果将甲、乙两人射击环数的平均数分别记作和 , 方差分别记作和 , 那么下列描述能说明甲运动员成绩较好且更稳定的是( )A、且 B、且 C、且 D、且5. 已知点在轴上,那么点的坐标为( )A、 B、 C、 D、6. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )
A、 B、 C、 D、4. 甲、乙两名射击运动员分别进行了相同次数的射击训练,如果将甲、乙两人射击环数的平均数分别记作和 , 方差分别记作和 , 那么下列描述能说明甲运动员成绩较好且更稳定的是( )A、且 B、且 C、且 D、且5. 已知点在轴上,那么点的坐标为( )A、 B、 C、 D、6. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )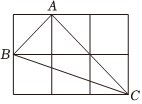 A、 B、 C、 D、7. 如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A、
A、 B、 C、 D、7. 如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A、 B、
B、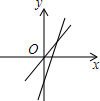 C、
C、 D、
D、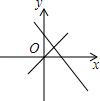 8. 下列命题中,真命题是( )A、若一个三角形的三边长分别是a、b、c,则有 B、(6,0)是第一象限内的点 C、所有的无限小数都是无理数 D、正比例函数()的图象是一条经过原点(0,0)的直线9. 小华和爸爸一起玩“掷飞镖”游戏.游戏规则:站在米开外朝飞镖盘扔飞镖,若小华投中次得分,爸爸投中次得分.结果两人一共投中了次,经过计算发现爸爸的得分比小华的得分多分.设小华投中的次数为 , 爸爸投中的次数为 , 根据题意列出的方程组正确的是( )A、 B、 C、 D、10. 甲、乙两车从地出发,匀速驶往地.乙车出发h后,甲车才沿相同的路线开始行驶.甲车先到达地并停留分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离与甲车行驶的时间x(h)的函数关系的图象,则( )
8. 下列命题中,真命题是( )A、若一个三角形的三边长分别是a、b、c,则有 B、(6,0)是第一象限内的点 C、所有的无限小数都是无理数 D、正比例函数()的图象是一条经过原点(0,0)的直线9. 小华和爸爸一起玩“掷飞镖”游戏.游戏规则:站在米开外朝飞镖盘扔飞镖,若小华投中次得分,爸爸投中次得分.结果两人一共投中了次,经过计算发现爸爸的得分比小华的得分多分.设小华投中的次数为 , 爸爸投中的次数为 , 根据题意列出的方程组正确的是( )A、 B、 C、 D、10. 甲、乙两车从地出发,匀速驶往地.乙车出发h后,甲车才沿相同的路线开始行驶.甲车先到达地并停留分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离与甲车行驶的时间x(h)的函数关系的图象,则( ) A、甲车的速度是 B、 , 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇
A、甲车的速度是 B、 , 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇二、填空题:本题共5小题,每小题3分,共15分。
-
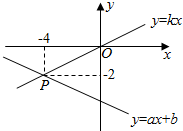
11. 25的平方根是 .12. 将直线沿轴向上平移个单位,可得直线的解析式 .13. 如图,已知直线和直线交于点 , 则关于 , 的二元一次方程组的解是 .
 14. 已知和关于轴对称,则的值为 .15. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .
14. 已知和关于轴对称,则的值为 .15. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .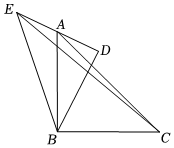
三、解答题:本题共7小题,共55分。解答应写出文字说明,证明过程或演算步骤。
-
16. 计算:
(1)、;(2)、17. 解方程组:
(1)、;(2)、 .18. 如图在平面直角坐标系中,已知的顶点坐标分别是 , , . (1)、画出关于轴对称的 , 其中点的对应点是点 , 点的对应点是点 , 并请直接写出点的坐标为 , 点的坐标为;(2)、请直接写出的面积是;(3)、已知点到两坐标轴距离相等,若 , 则请直接写出点的坐标为 .19. 已知:如图, , 和相交于点 , 是上一点,是上一点,
(1)、画出关于轴对称的 , 其中点的对应点是点 , 点的对应点是点 , 并请直接写出点的坐标为 , 点的坐标为;(2)、请直接写出的面积是;(3)、已知点到两坐标轴距离相等,若 , 则请直接写出点的坐标为 .19. 已知:如图, , 和相交于点 , 是上一点,是上一点,
且 . (1)、求证:;(2)、若 , , 求的度数.20. 为了解八年级学生的体质健康状况,某校对八年级班名同学进行了体质检测满分分,最低分 , 并按照男女把成绩整理如图:
(1)、求证:;(2)、若 , , 求的度数.20. 为了解八年级学生的体质健康状况,某校对八年级班名同学进行了体质检测满分分,最低分 , 并按照男女把成绩整理如图:
八年级班体质检测成绩分析表平均数
中位数
众数
方差
男生
女生
(1)、求八年级班的女生人数;(2)、根据统计图可知, , , ;(3)、若该校八年级一共有人,则估计得分在分及分以上的人数共有多少人?21. 根据以下信息,探索完成任务:如何设计招聘方案?
素材
某汽车制造厂开发一款新式电动汽车,计划一年生产安装辆每名熟练工均能独立安装电动汽车,由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人,经过培训上岗可以独立进行安装.
素材
调研部门发现:名熟练工和名新工人每月可安装辆电动汽车;名熟练工和名新工人每月可安装辆电动汽车.
素材
工厂给安装电动汽车的每名熟练工每月发元工资,每名新工人每月发元工资.
(1)、【任务一分析数量关系】每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、【任务二:确定可行方案】如果工厂招聘名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种工人的招聘方案?(3)、【任务三:选取最优方案】在上述方案中,为了节省成本,应该招聘新工人 名直接写出答案22. 如图,直线与坐标轴分别交于点 , , 以为边在轴的右侧作正方形 . (1)、求点 , 的坐标;(2)、如图,点是轴上一动点,点在的右侧, , .
(1)、求点 , 的坐标;(2)、如图,点是轴上一动点,点在的右侧, , .
探究发现,点在一条定直线上,请直接写出该直线的解析式_▲_ ;
若点是线段的中点,另一动点在直线上,且 , 请求出点的坐标.