广东省深圳市福田区明德重点中学2023-2024学年七年级(上)期末数学试卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 有理数的相反数是( )A、 B、 C、 D、2. 中国信息通信研究院测算,年,中国商用带动的信息消费规模将超过万亿元,直接带动经济总产出达万亿元.其中数据万亿用科学记数法表示为( )A、 B、 C、 D、3. 榫卯是我国古代建筑、家具的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,如图是其中一种榫,其主视图是( )
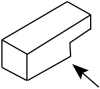 A、
A、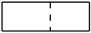 B、
B、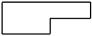 C、
C、 D、
D、 4. 下面调查方式中,合适的是( )A、神舟十五号飞船发射前的零件检查,选择抽样调查方式 B、调查某新型防火材料的防火性能,采用全面调查的方式 C、为了了解某旅游景点全年的游客流量,选择抽样调查的方式 D、对乘坐某班次飞机的乘客进行安检,采用抽样调查的方式5. 如图, , , 平分 , 则的度数为( )
4. 下面调查方式中,合适的是( )A、神舟十五号飞船发射前的零件检查,选择抽样调查方式 B、调查某新型防火材料的防火性能,采用全面调查的方式 C、为了了解某旅游景点全年的游客流量,选择抽样调查的方式 D、对乘坐某班次飞机的乘客进行安检,采用抽样调查的方式5. 如图, , , 平分 , 则的度数为( ) A、 B、 C、 D、6. 下列判断正确的是( )A、与不是同类项 B、和都是单项式 C、单项式的次数是3,系数是0 D、是三次三项式7. 某学校七年级进行一次徒步活动,带队教师和学生们以的速度从学校出发,后,小王骑自行车前去追赶如果小王以的速度行驶,那么小王要用多少小时才能追上队伍?设小王要用才能追上队伍,那么可列出的方程是( )A、 B、 C、 D、8. 实数 , 在数轴上的位置如图所示,下列各式正确的是( )
A、 B、 C、 D、6. 下列判断正确的是( )A、与不是同类项 B、和都是单项式 C、单项式的次数是3,系数是0 D、是三次三项式7. 某学校七年级进行一次徒步活动,带队教师和学生们以的速度从学校出发,后,小王骑自行车前去追赶如果小王以的速度行驶,那么小王要用多少小时才能追上队伍?设小王要用才能追上队伍,那么可列出的方程是( )A、 B、 C、 D、8. 实数 , 在数轴上的位置如图所示,下列各式正确的是( ) A、 B、 C、 D、9. 已知代数式的值为 , 则代数式的值为( )A、 B、 C、 D、10. 定义:从的顶点出发,在角的内部引一条射线 , 把分成:的两部分,射线叫做的三等分线若在中,射线是的三等分线,射线是的三等分线,设 , 则用含的代数式表示为( )A、或或 B、或或 C、或或 D、或或
A、 B、 C、 D、9. 已知代数式的值为 , 则代数式的值为( )A、 B、 C、 D、10. 定义:从的顶点出发,在角的内部引一条射线 , 把分成:的两部分,射线叫做的三等分线若在中,射线是的三等分线,射线是的三等分线,设 , 则用含的代数式表示为( )A、或或 B、或或 C、或或 D、或或二、填空题:本题共5小题,每小题3分,共15分。
-
11. 已知是方程的解,则 .12. 一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“祥”相对的面上所写的字是 .
 13. 如图是一个数值转换机,如果输出的结果为 , 那么输入的数是 .
13. 如图是一个数值转换机,如果输出的结果为 , 那么输入的数是 . 14. 已知线段 , 直线上有点 , 且 , 是线段的中点,则 .15. 如图,用大小相同的小正方形拼图形,第个图形是一个小正方形;第个图形由个小正方形拼成;第个图形由个小正方形拼成,依此规律,若第个图形比第个图形多用了个小正方形,则的值是 .
14. 已知线段 , 直线上有点 , 且 , 是线段的中点,则 .15. 如图,用大小相同的小正方形拼图形,第个图形是一个小正方形;第个图形由个小正方形拼成;第个图形由个小正方形拼成,依此规律,若第个图形比第个图形多用了个小正方形,则的值是 .
三、计算题:本大题共2小题,共16分。
-
16. 先化简,再求值:
(1)、 , 其中 .(2)、 , 其中 .17. 如图所示, 分别平分 和 ,且 . (1)、如果 ,求 的度数;(2)、如果 ,求 的度数.
(1)、如果 ,求 的度数;(2)、如果 ,求 的度数.四、解答题:本题共5小题,共39分。解答应写出文字说明,证明过程或演算步骤。
-
18. 计算:
(1)、;(2)、 .19. 解下列方程:
(1)、;(2)、 .20. 我市某中学开展“厉行勤俭节约,反对铺张浪费”主题活动,为了解学生的参与情况,小明在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行了调查将调查内容分为四组:饭和菜全部吃完;有剩饭但菜吃完;饭吃完但菜有剩;饭和菜都有剩根据调查结果,绘制了如图所示两幅尚不完整的统计图,回答下列问题: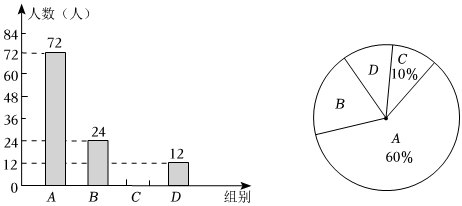 (1)、这次被抽查的学生共有 人,扇形统计图中,“组”所对圆心角的度数为 ;(2)、直接补全条形统计图;(3)、已知该中学共有学生人,请估计这日午饭有剩饭的学生人数;若有剩饭的学生按平均每人剩克米饭计算,这日午饭将浪费多少千克米饭?21. 第九届亚洲冬季运动会于年在中国黑龙江省哈尔滨市举行,为了迎接亚洲冬季运动会,现要修一条公路,甲工程队单独修需天完成,乙工程队单独完成需要的天数是甲工程单独完成天数的少天.(1)、乙工程队单独完成需要多少天?(2)、若甲先单独修天,之后甲乙合作修完这条公路,求甲乙还需合作几天修完这条路?22. 如图,在数轴上原点表示数 , 点表示数是 , 点表示的数是 , 且点在原点右侧,点在原点的左侧,点到原点距离个单位长度. , 满足式子 .
(1)、这次被抽查的学生共有 人,扇形统计图中,“组”所对圆心角的度数为 ;(2)、直接补全条形统计图;(3)、已知该中学共有学生人,请估计这日午饭有剩饭的学生人数;若有剩饭的学生按平均每人剩克米饭计算,这日午饭将浪费多少千克米饭?21. 第九届亚洲冬季运动会于年在中国黑龙江省哈尔滨市举行,为了迎接亚洲冬季运动会,现要修一条公路,甲工程队单独修需天完成,乙工程队单独完成需要的天数是甲工程单独完成天数的少天.(1)、乙工程队单独完成需要多少天?(2)、若甲先单独修天,之后甲乙合作修完这条公路,求甲乙还需合作几天修完这条路?22. 如图,在数轴上原点表示数 , 点表示数是 , 点表示的数是 , 且点在原点右侧,点在原点的左侧,点到原点距离个单位长度. , 满足式子 .
 (1)、求 , 的值;(2)、若动点从点出发,以每秒个单位长度的速度沿数轴向左运动:同时动点从点出发以每秒个单位长度的速度沿着数轴向右运动,求两点运动时间为何值时,线段的长为个单位长度.(3)、若动点从点出发沿数轴向左运动,到达原点之前的速度为每秒个单位长度,到达原点之后的速度为每秒个单位长度;同时动点从点出发以每秒个单位长度的速度沿着数轴向右运动,求两点运动时间为何值时,、两点到原点的距离相等.
(1)、求 , 的值;(2)、若动点从点出发,以每秒个单位长度的速度沿数轴向左运动:同时动点从点出发以每秒个单位长度的速度沿着数轴向右运动,求两点运动时间为何值时,线段的长为个单位长度.(3)、若动点从点出发沿数轴向左运动,到达原点之前的速度为每秒个单位长度,到达原点之后的速度为每秒个单位长度;同时动点从点出发以每秒个单位长度的速度沿着数轴向右运动,求两点运动时间为何值时,、两点到原点的距离相等.