广东省深圳市2023-2024学年上学期12月九年级适应性考试模拟数学试卷
试卷更新日期:2024-03-04 类型:月考试卷
一、单选题(共30分)
-
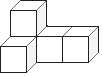
1. 如图,由5个相同正方体组合而成的几何体,它的主视图是( )
 A、
A、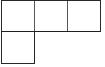 B、
B、 C、
C、 D、
D、 2. 某工厂由于采用新技术,生产量逐月增加,原来月产量为2000件,两个月后增至月产量为3000件. 若设月平均增长率为x , 则下列所列的方程正确的是( )A、 B、 C、 D、3. 如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形 沿 对开后,再把矩形 沿 对开,依此类推.若各种开本的矩形都相似,那么 等于( ).
2. 某工厂由于采用新技术,生产量逐月增加,原来月产量为2000件,两个月后增至月产量为3000件. 若设月平均增长率为x , 则下列所列的方程正确的是( )A、 B、 C、 D、3. 如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形 沿 对开后,再把矩形 沿 对开,依此类推.若各种开本的矩形都相似,那么 等于( ). A、 B、 C、 D、4. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.作.若 , 则的值为( )
A、 B、 C、 D、4. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.作.若 , 则的值为( ) A、 B、 C、 D、15. 如图,点A、B、C在一条直线上,和均为正三角形,AE、BD分别与CD、CE交于点M、N , 有如下结论:①;②;③;④;⑤AE与DB所夹锐角为60°.其中正确的有(
A、 B、 C、 D、15. 如图,点A、B、C在一条直线上,和均为正三角形,AE、BD分别与CD、CE交于点M、N , 有如下结论:①;②;③;④;⑤AE与DB所夹锐角为60°.其中正确的有( A、5个 B、4个 C、3个 D、2个6. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、7. 从上面看如图所示的几何体,得到的图形是( )
A、5个 B、4个 C、3个 D、2个6. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、7. 从上面看如图所示的几何体,得到的图形是( )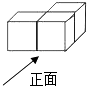 A、
A、 B、
B、 C、
C、 D、
D、 8. 用配方法解方程时,配方结果正确的是( )A、 B、 C、 D、9. 如果关于x的一元二次方程x2﹣6x+2k=0有两个实数根,那么实数k的取值范围是( )A、k≤ B、k C、k D、k10. 如图为西周时期的“凤鸟纹饰”玉琮,其形对称,呈扁矮方柱状,内圆外方,前后穿圆孔,两端留有短射,蕴含古人“壁圆象天,琮方象地”的天地思想.下列是该玉琮主视图的是( )
8. 用配方法解方程时,配方结果正确的是( )A、 B、 C、 D、9. 如果关于x的一元二次方程x2﹣6x+2k=0有两个实数根,那么实数k的取值范围是( )A、k≤ B、k C、k D、k10. 如图为西周时期的“凤鸟纹饰”玉琮,其形对称,呈扁矮方柱状,内圆外方,前后穿圆孔,两端留有短射,蕴含古人“壁圆象天,琮方象地”的天地思想.下列是该玉琮主视图的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(共15分)
-
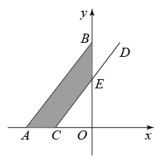
11. 如图,在平面直角坐标系中,点A在x轴上,点B(0,9),线段AB向右平移3个单位至线段CD,线段CD与y轴交于点E,若图中阴影部分面积是21,则点C的坐标为 .
 12. 已知在中, , , , 那么 .13. 一次函数y=-x+1与反比例函数 (k<0)中,x与y的部分对应值如下表:
12. 已知在中, , , , 那么 .13. 一次函数y=-x+1与反比例函数 (k<0)中,x与y的部分对应值如下表:x
-3
-2
-1
1
2
3
y=-x+1
4
3
2
0
-1
-2
1
2
-2
-1
-
则不等式 >0的解集为.
14. 已知一元二次方程x2-4x-3=0两根为x1、x2 , 则x1x2= .15. 要为一幅长 . 宽为的照片配一个相框(相框不遮挡照片),要求相框的四条边宽度相等,且相框所占面积为照片面积的四分之一,相框边的宽度应是多少厘米?设相框边的宽度是 , 则列出的方程应为 .三、解答题(共20分)
-
16. 解方程:(1)、;(2)、 .17. 解下列方程或解不等式组:(1)、(2)、(3)、18. 如图:小明想测量一棵树的高度AB,在阳光下,小明测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长CD为1.5米,落在地面上的影长BD为3米,则树高AB为多少米.

 19. 如图,一次函数与反比例函数的图象交于 , 两点.
19. 如图,一次函数与反比例函数的图象交于 , 两点. (1)、求反比例函数与一次函数的解析式;(2)、过点A作轴,垂足为C , 求的面积 .20. 某著名的旅游城市2016年“十一”黄金周期间,接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次.(1)、求出2016年至2018年十一长假期间游客人次的年平均增长率;(2)、该市一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗6元,借鉴以往经验:若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗.若规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家能实现每天盈利6300元?21.(1)、问题发现:如图1,在等边 中,点 为 边上一动点, 交 于点 ,将 绕点 顺时针旋转 得到 ,连接 .则 与 的数量关系是 , 的度数为.
(1)、求反比例函数与一次函数的解析式;(2)、过点A作轴,垂足为C , 求的面积 .20. 某著名的旅游城市2016年“十一”黄金周期间,接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次.(1)、求出2016年至2018年十一长假期间游客人次的年平均增长率;(2)、该市一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗6元,借鉴以往经验:若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗.若规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家能实现每天盈利6300元?21.(1)、问题发现:如图1,在等边 中,点 为 边上一动点, 交 于点 ,将 绕点 顺时针旋转 得到 ,连接 .则 与 的数量关系是 , 的度数为.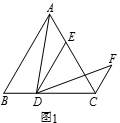 (2)、拓展探究:如图2,在 中, , ,点 为 边上一动点, 交 于点 ,当∠ADF=∠ACF=90°时,求 的值.
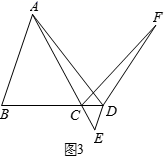
(2)、拓展探究:如图2,在 中, , ,点 为 边上一动点, 交 于点 ,当∠ADF=∠ACF=90°时,求 的值.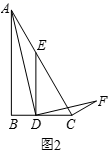 (3)、解决问题:如图3,在 中, ,点 为 的延长线上一点,过点 作 交 的延长线于点 ,直接写出当 时 的值.
(3)、解决问题:如图3,在 中, ,点 为 的延长线上一点,过点 作 交 的延长线于点 ,直接写出当 时 的值.