浙江省嘉兴市2023-2024学年七年级上学期期末考试模拟卷数学试卷

试卷更新日期：2024-03-04 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 数a的相反数为2023，则a的值为（）

A、2023 B、 $- 2023$ C、 $- \frac{1}{2023}$ D、 $\frac{1}{2023}$

查看试题解析
2. 杭州亚运体育场俗称“大莲花”，总建筑面积约 216000平方米，将216000平方米用科学记数法表示为（）

A、 $21.6 \times 1 0^{5}$ 平方米 B、 $2.16 \times 1 0^{6}$ 平方米 C、 $2.16 \times 1 0^{5}$ 平方米 D、 $2.16 \times 1 0^{7}$ 平方米

查看试题解析
3. 在实数3.14， $\sqrt{0.04}$ ， $\frac{2}{9}$ ， $\frac{π}{2}$ 中，属于无理数的是（）

A、3.14 B、 $\sqrt{0.04}$ C、 $\frac{2}{9}$ D、 $\frac{π}{2}$

查看试题解析
4. 下列化简正确的是（）

A、 $8 x - 7 y = x - y$ B、 $2 a^{2} b^{2} - a b = a b$ C、 $9 a^{2} b - 4 b a^{2} = 5 a^{2} b$ D、 $5 m - 4 m = 1$

查看试题解析
5. 已知关于x的方程3x+2a=2的解是x=1，则a的值是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $- \frac{5}{2}$ D、 $\frac{5}{2}$

查看试题解析
6. 下列说法：
①在所有连结两点的线中，线段最短；
②连接两点的线段叫做这两点的距离；
③若线段 $A C = B C$ ，则点C是线段AB的中点；
④经过刨平的木板上的两个点，能弹出一条笔直的墨线，是因为两点确定一条直线．
其中说法正确的是（）

A、①②③ B、①④ C、②③ D、①②③④

查看试题解析
7. 如果代数式 $a - 2 b$ 的值为4，那么代数式 $4 b - 2 a - 3$ 的值等于（）

A、 $- 11$ B、 $- 7$ C、7 D、1

查看试题解析
8. 如图，点C把线段AB从左至右依次分成2：3两部分，点D是AB的中点，若CD＝2，则线段AB的长是（）

A、10 B、15 C、20 D、25

查看试题解析
9. 某商店在某一时间以每件90元的价格出售两件商品，其中一件盈利25%，另一件亏损25%，则在这次买卖中，商家（）

A、亏损8元 B、赚了12元 C、亏损了12元 D、不亏不损

查看试题解析
10. 如图所示，在这个数据运算程序中，若开始输入的x的值为5，
第1次运算结果输出的是8，返回进行第二次运算输出的是4，…，
则第2022次输出的结果是（）

A、1 B、2 C、4 D、8

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 化简： $\sqrt{4}$ = ．

查看试题解析
12. 已知单项式 $- \frac{4}{3} a^{n} b^{3}$ 与单项式 $- 2 a^{2} b^{m - 2}$ 是同类项，则 $m - n =$ ．

查看试题解析
13. 如图，点C、D在线段AB上，点C为AB中点，若AC=5cm，BD=2cm，则CD=cm．

查看试题解析
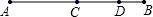14. 现规定一种新的运算： $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，若 $| \begin{array}{l} 3 & 3 \\ 2 - x & 4 \end{array} | = 9$ ，则 $x =$ .

查看试题解析
15. 某次数学竞赛共有20道题，已知做对一道得4分，做错一道或者不做扣1分，某同学最后的得分是50分，则他做对道题．

查看试题解析
16. 如图所示，用火柴拼成一排由 $6$ 个三角形组成图形，需要根火柴棒，小亮用 $2023$ 根火柴棒，可以拼出个三角形．

查看试题解析

三、解答题（本题有8小题，第17~22题每题6分，第23、24题每题8分，共52分）

17. 计算：

(1)、 $(- 1)^{2} + \sqrt[3]{- 27} + | - 2 |$

(2)、 $(- 6)^{2} \times (\frac{1}{3} - \frac{1}{2}) - 2^{3}$

查看试题解析
18. 解方程：

(1)、 $4 x - 3 = 2 (x - 1)$

(2)、 $\frac{x}{6} - \frac{30 - x}{4} = 15$

查看试题解析
19. 如图，已知 $A$ ， $B$ 是直线 $l$ 上两点， $C$ 是直线 $l$ 外一点．

(1)、画射线 $A C$ ，线段 $B C$ ；

(2)、过点 $C$ 作 $l$ 的垂线段．

查看试题解析
20. 先化简，再求值： $\frac{1}{2} a - 2 (a - \frac{1}{3} b^{2}) + (- \frac{3}{2} a + \frac{1}{3} b^{2})$ ，其中 $a = - 3$ ， $b = - \frac{1}{2}$ ．

查看试题解析
21. 某市为鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过40立方米时，按2元/立方米计费；月用水量超过40立方米时，其中的40立方米仍按2元/立方米收费，超过部分按3.5元/立方米计费.设每户家庭月用水量为x立方米.

(1)、当x不超过40时，应收水费为（用x的代数式表示）；当x超过40时，应收水费为（用x的代数式表示化简后的结果）；

(2)、小明家四月份用水26立方米，五月份用水52立方米，请帮小明计算一下他家这两个月一共应交多少元水费？

(3)、小明家六月份交水费150元，请帮小明计算一下他家这个月用水量多少立方米？

查看试题解析
22. 如图，点C为线段AD上一点，点B为CD的中点，且AD＝13cm，BC＝3cm．

(1)、图中共有条线段；

(2)、求AC的长；

(3)、若点E在直线AD上，且EA＝4cm，求BE的长．

查看试题解析
23. 如图1，已知，点 $O$ 为直线 $A B$ 上一点， $O C$ 在直线 $A B$ 是上方， $∠ A O C = 60 °$ ．一直角三角板的直角顶点放在点 $O$ 处，三角板一边 $O M$ 在射线 $O B$ 上，另一边 $O N$ 在直线 $A B$ 的下方．

(1)、在图1的时刻， $∠ B O C$ 的度数为 $°$ ， $∠ C O N$ 的度数为 $°$ ；

(2)、如图2，当三角板绕点 $O$ 旋转至一边 $O M$ 恰好平分 $∠ B O C$ 时， $∠ B O N$ 的度数为 $°$ ；

(3)、如图3，当三角板绕点 $O$ 旋转至一边 $O N$ 在 $∠ A O C$ 的内部时， $∠ A O M - ∠ C O N$ 的度数为 $°$ ；

(4)、在三角板绕点 $O$ 旋转一周的过程中， $∠ C O M$ 与 $∠ A O N$ 的关系为．

查看试题解析
24. 数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合，
研究数轴我们发现了许多重要的规律．

(1)、【特例感知】：若数轴上点A ，点B表示的数分别为5， $- 7$ ，
则A ， B两点之间的距离为，线段 $A B$ 的中点表示的数为；

(2)、①【分类讨论】：若数轴上点A ，点B表示的数分别为a ， b ，
当 $a > b > 0$ ，则A ， B两点之间的距离为 $A B = a - b$ ；
当 $a > 0 > b$ ，则A ， B两点之间的距离为 $A B = a - b$ ；
当 $0 > a > b$ ，则A ， B两点之间的距离为 $A B =$ ；
②【类比探究】：线段 $A B$ 的中点表示的数为（用含a ， b的代数式表示）；

(3)、【综合运用】：若数轴上点A ，点B表示的数分别为5， $- 7$ ，
点M从点A出发，以每秒1个单位长度的速度向左匀速运动，
同时，点N从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，
当M ， N两点相遇时，均停止运动，设运动时间为t秒（ $t > 0$ ），点M ， N在运动过程中；
①M ， N两点之间的距离为；（用含t的代数式表示）
②若点C为 $A M$ 的中点，点D为 $B N$ 的中点，线段 $C D$ 的长度为（用含t的代数式表示）．

查看试题解析