广东省茂名市高州市2023-2024学年八年级上学期期末数学试卷

试卷更新日期：2024-03-04 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 在下列实数中，无理数是（）

A、 $\frac{1}{3}$ B、 $\sqrt{2}$ C、 $0$ D、 $9$

查看试题解析
2. 下列各点在第一象限的是（）

A、 $(3 ， - 2)$ B、 $(- 3 ， - 2)$ C、 $(3 ， 2)$ D、 $(- 1 ， 2)$

查看试题解析
3. 下列各式正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{(- 3)^{2}} = - 3$ C、 $\sqrt[3]{4} = 2$ D、 $\pm \sqrt{25} = \pm 5$

查看试题解析
4. ${\begin{array}{l} x = 5 \\ y = 3 \end{array}$ 是下面哪个二元一次方程的解（）

A、 $2 x - y = 7$ B、 $y = - x + 2$ C、 $x = - y - 2$ D、 $2 x - 3 y = - 1$

查看试题解析
5. 下列画出的直线a与b不一定平行的是（）

A、 B、 C、 D、

查看试题解析
6. 小明同学随机调查七 $(2)$ 班 $6$ 名同学每天食堂午饭消费金额，制作如下统计表：
类别
同学 $1$
同学 $2$
同学 $3$
同学 $4$
同学 $5$
同学 $6$
金额 $($ 元 $)$
     $5$
     $6$
     $5$
     $6$
     $6$
     $8$
则这组消费金额（）

A、平均数为 $5$ B、中位数为 $5$ C、众数为 $6$ D、方差为 $6$

查看试题解析
7. 下列各式中，是最简二次根式的是（）

A、 $\sqrt{0.3}$ B、 $\sqrt{10}$ C、 $\sqrt{20}$ D、 $\sqrt{24}$

查看试题解析
8. 如图，矩形纸片 $A B C D$ ， M为 $A D$ 边的中点将纸片沿 $B M 、 C M$ 折叠，使A点落在 $A_{1}$ 处，D点落在 $D_{1}$ 处，若 $∠ 1 = 32 °$ ，则 $∠ B M C =$ （）

A、 $74 °$ B、 $106 °$ C、 $122 °$ D、 $148 °$

查看试题解析
9. 直线 $y = - k x + k$ 与直线 $y = k x$ 在同一坐标系中的大致图象可能是图中（）

A、 B、 C、 D、

查看试题解析
10. 如图是一块在电脑屏幕上出现的长方形色块图，由 6 个不同颜色的正方形组成，已知中间最小的一个正方形的边长为 1，那么这个长方形色块图的周长为（）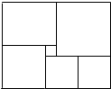

A、42 B、48 C、44 D、50

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分。

11. $\sqrt{2} + \sqrt{\frac{1}{2}} =$ ．

查看试题解析
12. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的 $.$ 如图， $∠ 1 = 122 ° 13'$ ，则 $∠ 2$ 的度数为．

查看试题解析
13. 如图，直线 $y = 2 x$ 与 $y = k x + b$ 相交于点 $P (1 ， 2)$ ，则关于 $x$ 的方程 $k x + b = 2 x$ 的解是．

查看试题解析
14. 一水池的容积是90m³ ，现蓄水10m³ ，用水管以5m³/h的速度向水池注水，直到注满为止写出蓄水量V（m³）与注水时间t（h）之间的关系式（指出自变量t的取值范围）．

查看试题解析
15. “三等分一个任意角”是数学史上一个著名问题 $.$ “今天人们已经知道，仅用圆规和直尺是不可能作出的，在探索中，有人曾利用过如图所示的图形，其中， $A B C D$ 是长方形， $F$ 是 $D A$ 延长线上一点， $G$ 是 $C F$ 上一点，并且 $∠ A C G = ∠ A G C$ ， $∠ G A F = ∠ F .$ 若 $∠ F = 15 °$ ， $G F = 4$ ，则长方形 $A B C D$ 的面积为．

查看试题解析

三、计算题：本大题共1小题，共6分。

16. 解方程组： ${\begin{array}{l} 3 x + 2 y = 7 \\ 4 x - y = 13 \end{array}$

查看试题解析

四、解答题：本题共8小题，共69分。解答应写出文字说明，证明过程或演算步骤。

17. 计算：
$\sqrt[3]{27} + (- 3)^{0} - \sqrt{8} + | - 2 \sqrt{2} | .$

查看试题解析
18. 为了弘扬爱国主义精神，实验中学在五四青年节，组织了唱红歌活动，八 $(3)$ 班选定了三人合唱小组，排练时歌手 $A$ ， $B$ ， $C$ 的站位如图所示：

(1)、如果 $A$ 点的坐标为 $(0 ， 0)$ ， $B$ 点的坐标为 $(2 ， 4)$ ，则 $C$ 点的坐标为；

(2)、在（1）的坐标系下，连结 $A B$ ， $A C$ ， $B C$ ，求出 $△ A B C$ 的面积；

(3)、在（1）的坐标系下，歌手 $B$ 保持不动，将歌手 $A$ 向上平移 $1$ 个单位后再向右平移 $1$ 个单位到 $A'$ ，将歌手 $C$ 向上平移 $2$ 个单位到 $C'$ ，请判断由 $A'$ ， $B$ ， $C'$ 三点构成的三角形是否为直角三角形？为什么？

查看试题解析
19. 已知：如图， $B C ⊥ A C$ 于点 $C$ ， $C D ⊥ A B$ 于点 $D$ ， $∠ E B C = ∠ A$ ，求证： $B E / / C D$ ．

查看试题解析
20. 如图，大拇指与小拇指尽量张开时，两指尖的距离称为“指距”，研究表明，一般情况下人的身高 $h (c m)$ 是指距 $d (c m)$ 的一次函数，
【测量数据】测量数据如表：
指距 $d (c m)$
20
21
22
23
身高 $h (c m)$
160
169
178
187

(1)、【关系探究】
根据表中数据，求h与d之间的函数关系式；

(2)、【结论应用】
我国篮球运动员周琦的身高约为 $217 c m$ ，估算他的指距是多少？（结果精确到 $0.1 c m$ ）

查看试题解析

21. 某校八

(5)

班小唐同学为了解

2022

年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，

月均用水量 $x (t)$	频数 $($ 户 $)$	频率
$0 < x \leq 5$	$6$	$0.12$
$5 < x \leq 10$	$a$	$0.24$
$10 < x \leq 15$	$16$	$0.32$
$15 < x \leq 20$	$10$	$0.20$
$20 < x \leq 25$	$4$	$b$
$25 < x \leq 30$	$2$	$0.04$

请根据图表提供的信息，解答下列问题：

(1)、在频数分布表中，求出

a =

_▲__，

b =

_▲_，并补全频数分布直方图；

(2)、求该小区用水量不超过

20 t

的家庭占被调查家庭总数的百分比；

(3)、若该小区有

500

户家庭，根据小明的调查数据请估计该小区月均用水量超过

25 t

的家庭大约有多少户？

查看试题解析

22. 综合与实践活动中，为了测量学校旗杆的高度，小明设计了一个方案：如图，将升旗的绳子拉直到末端刚好接触地面，测得此时绳子末端距旗杆底端距离为 $2 m$ ，然后将绳子末端拉直到距离旗杆 $8 m$ 处，测得此时绳子末端距离地面高度为 $2 m$ ，求旗杆的高度 $. ($ 滑轮上方的部分忽略不计 $)$

查看试题解析
23. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具，某汽车销售公司计划购进一批新能源汽车进行销售，据了解， $3$ 辆 $A$ 型汽车、 $4$ 辆 $B$ 型汽车的进价共计 $115$ 万元； $4$ 辆 $A$ 型汽车、 $3$ 辆 $B$ 型汽车的进价共计 $130$ 万元．

(1)、求 $A 、 B$ 两种型号的汽车每辆进价分别为多少万元？

(2)、若该公司计划正好用 $150$ 万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），销售 $1$ 辆 $A$ 型汽车可获利 $6000$ 元，销售 $1$ 辆 $B$ 型汽车可获利 $4000$ 元，求该公司共有几种购买方案？假如这些新能源汽车全部售出，最大利润是多少元？

查看试题解析
24. 如图1，在平面直角坐标系中，直线 $l$ 与 $x$ 轴交于点 $A (- 8 ， 0)$ ，与 $y$ 轴交于点 $B (0 ， 6)$ ，点 $P$ 在 $x$ 轴上运动，连接 $P B$ ，将 $△ O B P$ 沿直线 $B P$ 折叠，点 $O$ 的对应点记为 $O'$ ．

(1)、求直线 $l$ 的函数表达式；

(2)、若点 $O'$ 恰好落在直线 $A B$ 上，求 $△ A B P$ 的面积；

(3)、如图2，若 $O' B$ 恰好与 $x$ 轴平行，且边 $O' P$ 与线段 $A B$ 有交点，设交点为 $C$ ，在 $y$ 轴上是否存在点 $Q$ ，使得 $△ B C Q$ 是等腰三角形？若存在，请直接写出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析

类别	同学 $1$	同学 $2$	同学 $3$	同学 $4$	同学 $5$	同学 $6$
金额 $($ 元 $)$	$5$	$6$	$5$	$6$	$6$	$8$

指距 $d (c m)$	20	21	22	23
身高 $h (c m)$	160	169	178	187