广东省汕头市龙湖区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 中国新能源汽车发展迅速,下列各图是国产新能源汽车图标,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 分式 有意义的条件是( )A、x=-3 B、x≠-3 C、x≠3 D、x≠03. 下列多边形中,内角和等于的是( )A、
2. 分式 有意义的条件是( )A、x=-3 B、x≠-3 C、x≠3 D、x≠03. 下列多边形中,内角和等于的是( )A、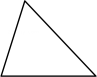 B、
B、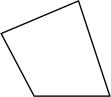 C、
C、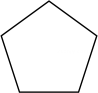 D、
D、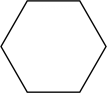 4. 下面运算正确的是( )A、7a2b-5a2b=2 B、x8÷x4=x2 C、(a-b)2=a2-b2 D、(2x2)3=8x65. 袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
4. 下面运算正确的是( )A、7a2b-5a2b=2 B、x8÷x4=x2 C、(a-b)2=a2-b2 D、(2x2)3=8x65. 袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( ) A、10cm B、15cm C、20cm D、25cm6. 我国古代数学家祖冲之发现的圆周率的分数近似值 , 称为密率,比的值只大 , 这个数用科学记数法可表示为( )A、 B、 C、 D、7. 阅读以下作图步骤:
A、10cm B、15cm C、20cm D、25cm6. 我国古代数学家祖冲之发现的圆周率的分数近似值 , 称为密率,比的值只大 , 这个数用科学记数法可表示为( )A、 B、 C、 D、7. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且8. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )
A、且 B、且 C、且 D、且8. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )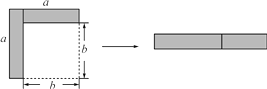 A、(a-b)2=a2-2ab+b2 B、a(a-b)=a2-ab C、(a-b)2=a2-b2 D、a2-b2=(a+b)(a-b)9. 如图所示,在△ABC中, , , DE为AB的中垂线, , 则CD的长是( )
A、(a-b)2=a2-2ab+b2 B、a(a-b)=a2-ab C、(a-b)2=a2-b2 D、a2-b2=(a+b)(a-b)9. 如图所示,在△ABC中, , , DE为AB的中垂线, , 则CD的长是( ) A、3 B、4 C、6 D、810. 如图,已知中高恰好平分边 , , 点是延长线上一动点,点是线段上一动点,且 , 下面的结论:
A、3 B、4 C、6 D、810. 如图,已知中高恰好平分边 , , 点是延长线上一动点,点是线段上一动点,且 , 下面的结论:①;
②的周长为;
③;
④ .
其中正确个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:本题共5小题,每小题3分,共15分。
-
11. 因式分解: = .12. 如图,点在的边的延长线上,若 , , 则的大小为 .
 13. 如图,点、在线段上,且 , , 若要使≌ , 则还需补充一个条件只需填一个答案即可
13. 如图,点、在线段上,且 , , 若要使≌ , 则还需补充一个条件只需填一个答案即可 14. 计算: .15. 人们把这个数叫做黄金比,著名数学家华罗庚优选法中的“法”就应用了黄金比. , , 记 , , 则 .
14. 计算: .15. 人们把这个数叫做黄金比,著名数学家华罗庚优选法中的“法”就应用了黄金比. , , 记 , , 则 .三、计算题:本大题共1小题,共7分。
-
16. 解分式方程: .
四、解答题:本题共8小题,共68分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算:
.
18. 如图,是的中点, , . 求证: . 19. 先化简,再求值 , 其中 .20. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .
19. 先化简,再求值 , 其中 .20. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .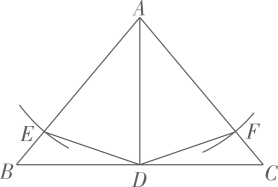 (1)、求证:;(2)、若 , 求的度数.21. 如图,三个顶点的坐标分别是 , , .
(1)、求证:;(2)、若 , 求的度数.21. 如图,三个顶点的坐标分别是 , , . (1)、请画出关于x轴对称的图形 , 并写出点的坐标;(2)、求的面积;(3)、在x轴上求一点P,使的值最小,通过画图直接画出点P.22. 某欧洲客商准备采购一批特色商品,下面是一段对话:
(1)、请画出关于x轴对称的图形 , 并写出点的坐标;(2)、求的面积;(3)、在x轴上求一点P,使的值最小,通过画图直接画出点P.22. 某欧洲客商准备采购一批特色商品,下面是一段对话:甲:用元采购型商品的件数是用元采购型商品的件数的倍;
乙:一件型商品的进价比一件型商品的进价多元.
(1)、根据对话信息,求一件 , 型商品的进价分别为多少元;(2)、若该欧洲客商购进 , 型商品共件进行试销,其中型商品的件数不大于型商品的件数,且不小于件,则共有哪几种进货方式?23. 综合与实践数学模型可以用来解决一类问题,是数学应用的基本途径通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
 (1)、发现问题:如图 , 在和中, , , , 连接 , , 延长交于点则与的数量关系: , ;(2)、类比探究:如图 , 在和中, , , , 连接 , , 延长 , 交于点请猜想与的数量关系及的度数,并说明理由;(3)、拓展延伸:如图 , 和均为等腰直角三角形, , 连接 , , 且点 , , 在一条直线上,过点作 , 垂足为点则 , , 之间的数量关系: .24. 综合与实践:
(1)、发现问题:如图 , 在和中, , , , 连接 , , 延长交于点则与的数量关系: , ;(2)、类比探究:如图 , 在和中, , , , 连接 , , 延长 , 交于点请猜想与的数量关系及的度数,并说明理由;(3)、拓展延伸:如图 , 和均为等腰直角三角形, , 连接 , , 且点 , , 在一条直线上,过点作 , 垂足为点则 , , 之间的数量关系: .24. 综合与实践:
【积累经验】我们在第十三章全等三角形中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题. 例如:我们在解决:如图 , 在中, , , 线段经过点 , 且于点 , 于点 .
求证: , 这个问题时,只要证明≌即可得到解决.
 (1)、请写出证明过程:(2)、【类比应用】
(1)、请写出证明过程:(2)、【类比应用】如图 , 在平面直角坐标系中, , , 点的坐标为 , 点的坐标为 , 求点的坐标.
(3)、【拓展提升】如图 , 在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为一边构造等腰直角三角形 , 直接写出在第一象限内满足条件的所有点的坐标 .
-