广东省深圳市龙岗区2023-2024学年八年级上学期期末数学仿真模拟试卷
试卷更新日期:2024-03-04 类型:期末考试
一、选择题(本部分共10小题,每小题3分,共30分)
-
1. 16的算术平方根是( )A、 ±4 B、±2 C、4 D、-42. 下列不能判定△ABC是直角三角形的是( )A、a2+b2-c2=0 B、a∶b∶c=3∶4∶5 C、∠A∶∠B∶∠C=3:4∶5 D、∠A+∠B=∠C3. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、4. 若是关于x 、y的二元一次方程ax-2y=1的解,则a的值为( )A、3 B、5 C、-3 D、-55. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )

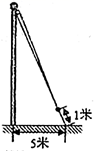 A、12 B、13 C、15 D、246. 在2023年元旦汇演中,10位评委给八年级一班比赛的打分如表格:
A、12 B、13 C、15 D、246. 在2023年元旦汇演中,10位评委给八年级一班比赛的打分如表格:成绩/分
94
95
96
97
98
99
评委人数
2
1
3
1
2
1
则这组数据的众数和中位数分别是( )
A、95,95 B、96,96 C、96,95 D、96,977. 如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D , 交AB于E , CD=3,则AD等于( )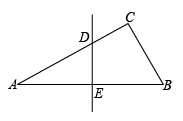 A、12 B、10 C、8 D、68. 函数与( , )在同一坐标系中的图象可能是( )A、
A、12 B、10 C、8 D、68. 函数与( , )在同一坐标系中的图象可能是( )A、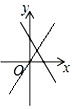 B、
B、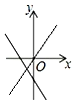 C、
C、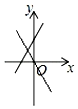 D、
D、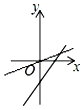 9. 如图,用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形,则每个小长方形的周长是( )
9. 如图,用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形,则每个小长方形的周长是( )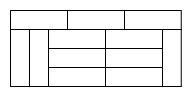 A、60厘米 B、80厘米 C、100厘米 D、120厘米10. 甲、乙两船沿直线航道AC匀速航行.甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行.设t小时后甲、乙两船与B处的距离分别为d1 , d2 , 则d1 , d2与t的函数关系如图.下列说法:
A、60厘米 B、80厘米 C、100厘米 D、120厘米10. 甲、乙两船沿直线航道AC匀速航行.甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行.设t小时后甲、乙两船与B处的距离分别为d1 , d2 , 则d1 , d2与t的函数关系如图.下列说法:①乙船的速度是40千米/时;
②甲船航行1小时到达B处;
③甲、乙两船航行0.6小时相遇;
④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的是( )
 A、①② B、①②③ C、①②④ D、①②③④
A、①② B、①②③ C、①②④ D、①②③④二、填空题(本部分共5小题,每小题3分,共15分,请将正确的答案填在答题卡上).
-
11. 的立方根是 .12. 某大学生招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,
已知小明数学得分为95分,物理得分为90分,那么小明的综合得分是分.
13. 如图,一次函数的图象与一次函数的图象相交于点 , 则关于,的方程组的解为 . 14. A , B两地相距20km , 甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.
14. A , B两地相距20km , 甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.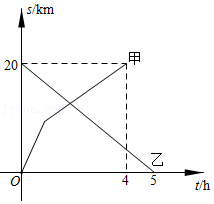 15. 如图,四边形是长方形纸片, , 对折长方形纸片 .
15. 如图,四边形是长方形纸片, , 对折长方形纸片 .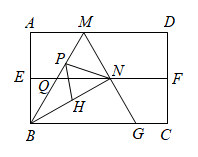
使与重合,折痕为 . 展平后再过点B折叠长方形纸片,
使点A落在上的点N , 折痕为 , 再次展平,连接 , ,
延长交于点G . 有如下结论:
①;
②;
③是等边三角形;
④P为线段上一动点,H是线段上的动点,则的最小值是 .
其中正确结论的序号是 .
三、解答题(本大题共7题.其中16题6分,17题7分,18题7分,19题8分,20题8分,21题10分,22题9分,共55分).
-
16. 计算:(1)、(2)、17. 解方程组:(1)、(2)、18. 某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现随机抽查了八年级20位同学捐款情况,并绘制出如下的统计表和统计图.根据上述信息,回答下列问题:
捐款(元)
20
50
100
150
200
人数(人)
4
8
n
2
1
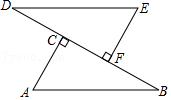
 (1)、 , ;(2)、学生捐款数目的众数是元,中位数是元,平均数是元;(3)、若该校有学生1500人,估计该校学生共捐款多少元?19. nbsp;. 如图,D、C、F、B四点在一条直线上,AB=DE , AC⊥BD于C , EF⊥BD于F , CD=BF .
(1)、 , ;(2)、学生捐款数目的众数是元,中位数是元,平均数是元;(3)、若该校有学生1500人,估计该校学生共捐款多少元?19. nbsp;. 如图,D、C、F、B四点在一条直线上,AB=DE , AC⊥BD于C , EF⊥BD于F , CD=BF .求证:AB∥DE .
 20. 为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,1只A型节能灯和3只B型节能灯共需26元.(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元.(2)、学校准备购买这两种型号的节能灯共200只,要求购买A型号的节能灯a只,记购买两种型号的节能灯的总费用为W元.
20. 为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,1只A型节能灯和3只B型节能灯共需26元.(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元.(2)、学校准备购买这两种型号的节能灯共200只,要求购买A型号的节能灯a只,记购买两种型号的节能灯的总费用为W元.①求W与a的函数关系式;
②当时,求购买两种型号的节能灯的总费用是多少?
21. 如图,直线L1: 与轴,轴分别交于A,B两点,点P( , 3)为直线AB上一点,另一直线L2:经过点P.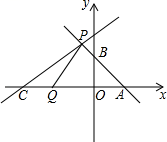 (1)、求点A、B坐标;(2)、求点P坐标和的值;(3)、若点C是直线L2与轴的交点,点Q是轴上一点,当△CPQ的面积等于3时,求出点Q的坐标22.(1)、[发现]:如图1.在△ABC中,AB=AC , ∠BAC=90°,过点A作AH⊥BC于点H ,
(1)、求点A、B坐标;(2)、求点P坐标和的值;(3)、若点C是直线L2与轴的交点,点Q是轴上一点,当△CPQ的面积等于3时,求出点Q的坐标22.(1)、[发现]:如图1.在△ABC中,AB=AC , ∠BAC=90°,过点A作AH⊥BC于点H ,求证:AH=BC .
 (2)、[拓展]:如图2.在△ABC和△ADE中,AB=AC , AD=AE , 且∠BAC=∠DAE=90°,点D、B、C在同一条直线上,AH为△ABC中BC边上的高,连接CE . 则∠DCE的度数为 , 同时猜想线段AH、CD、CE之间的数量关系,并说明理由.
(2)、[拓展]:如图2.在△ABC和△ADE中,AB=AC , AD=AE , 且∠BAC=∠DAE=90°,点D、B、C在同一条直线上,AH为△ABC中BC边上的高,连接CE . 则∠DCE的度数为 , 同时猜想线段AH、CD、CE之间的数量关系,并说明理由. (3)、[应用]:在图3、图4中.在△ABC中,AB=AC , 且∠BAC=90°,在同一平面内有一点P , 满足PC=1,PB=6,且∠BPC=90°,请求出点A到BP的距离.
(3)、[应用]:在图3、图4中.在△ABC中,AB=AC , 且∠BAC=90°,在同一平面内有一点P , 满足PC=1,PB=6,且∠BPC=90°,请求出点A到BP的距离.