2023年湖北省中考数学真题分类汇编：01 数与式

试卷更新日期：2024-03-04 类型：二轮复习

进入出卷网下载

一、选择题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、 $2$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、 $3 x^{2} + 2 x^{2} = 6 x^{4}$ B、 $(- 2 x^{2})^{3} = - 6 x^{6}$ C、 $x^{3} \cdot x^{2} = x^{6}$ D、 $- 6 x^{2} y^{3} \div 2 x^{2} y^{2} = - 3 y$

查看试题解析
3. 实数 $a$ 与 $b$ 在数轴上的位置如图所示，则它们的大小关系是（）

A、 $a > b$ B、 $a = b$ C、 $a < b$ D、无法确定

查看试题解析
4. 下列实数： $- 1$ ， 0， $\sqrt{2}$ ， $- \frac{1}{2}$ ，其中最小的是（　　）

A、 $- 1$ B、0 C、 $\sqrt{2}$ D、 $- \frac{1}{2}$

查看试题解析
5. 如图，数轴上点A所表示的数的相反数是（　　）

A、9 B、 $- \frac{1}{9}$ C、 $\frac{1}{9}$ D、 $- 9$

查看试题解析
6. 2023年全国普通高校毕业生规模预计达到1158万人，数11580000用科学记数法表示为（）

A、 $1.158 \times 1 0^{7}$ B、 $1.158 \times 1 0^{8}$ C、 $1.158 \times 1 0^{3}$ D、 $1158 \times 1 0^{4}$

查看试题解析
7. 实数10的相反数等于（）

A、-10 B、+10 C、 $- \frac{1}{10}$ D、 $\frac{1}{10}$

查看试题解析
8. 已知 $k = \sqrt{2} (\sqrt{5} + \sqrt{3}) \cdot (\sqrt{5} - \sqrt{3})$ ，则与 $k$ 最接近的整数为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 在实数－1， $\sqrt{3}$ ， $\frac{1}{2}$ ， 3.14中，无理数是（）

A、－1 B、 $\sqrt{3}$ C、 $\frac{1}{2}$ D、3.14

查看试题解析
10. 设有边长分别为a和b( $a > b$ )的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张．如图所示要拼一个边长为 $a + b$ 的正方形，需要1张A类纸片、1张B类纸片和2张C类纸片．若要拼一个长为 $3 a + b$ 、宽为 $2 a + 2 b$ 的矩形，则需要C类纸片的张数为（）

A、6 B、7 C、8 D、9

查看试题解析
11. 已知 $x^{2} - x - 1 = 0$ ，计算 $(\frac{2}{x + 1} - \frac{1}{x}) \div \frac{x^{2} - x}{x^{2} + 2 x + 1}$ 的值是（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析

12. 在日历上，某些数满足一定的规律．如图是某年8月份的日历，任意选择其中所示的含4个数字的方框部分，设右上角的数字为a，则下列叙述中正确的是（）．

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

A、左上角的数字为

a + 1

B、左下角的数字为

a + 7

C、右下角的数字为

a + 8

D、方框中4个位置的数相加，结果是4的倍数

查看试题解析

13. “五一”假期，宜昌旅游市场接待游客 $606.7$ 万人次，实现旅游总收入 $41.5$ 亿元．数据“ $41.5$ 亿”用科学记数法表示为（）．

A、 $415 \times 1 0^{7}$ B、 $41.5 \times 1 0^{8}$ C、 $4.15 \times 1 0^{9}$ D、 $4.15 \times 1 0^{10}$

查看试题解析
14. 下列运算正确的个数是（）．
① $| 2023 | = 2023$ ；② $2023 ° = 1$ ；③ $202 3^{- 1} = \frac{1}{2023}$ ；④ $\sqrt{202 3^{2}} = 2023$ ．

A、4 B、3 C、2 D、1

查看试题解析
15. 下列运算正确的是（）．

A、 $2 x^{4} \div x^{3} = 2 x$ B、 ${(x^{3})}^{4} = x^{7}$ C、 $x^{4} + x^{3} = x^{7}$ D、 $x^{3} \cdot x^{4} = x^{12}$

查看试题解析

二、填空题

16. 计算： $(- \frac{1}{3})^{- 2} + (1 - \sqrt{2})^{0} - 2 c o s 60 ° =$ ．

查看试题解析
17. 因式分解： $x (y - 1) + 4 (1 - y) =$ ．

查看试题解析
18. 观察下列两行数，探究第②行数与第①行数的关系：
$- 2$ ， 4， $- 8$ ， 16， $- 32$ ， 64，……①

0，7， $- 4$ ， 21， $- 26$ ， 71，……②

根据你的发现，完成填空：第①行数的第10个数为；取每行数的第2023个数，则这两个数的和为．

查看试题解析
19. 写出一个小于4的正无理数是．

查看试题解析
20. 计算； ${(- 1)}^{2} + {(\frac{1}{3})}^{0} =$ ．

查看试题解析
21. 若实数a、b分别满足a²-3a+2=0，b²-3b+2=0，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ = ．

查看试题解析
22. 计算 $4^{- 1} - \sqrt{\frac{1}{16}} + {(3 - \sqrt{2})}^{0}$ 的结果是．

查看试题解析
23. 若 $| a - 1 | + （ b - 3 ）^{2} = 0$ ，则 $\sqrt{a + b}$ = ．

查看试题解析
24. 若 $x + y = 3$ ， $x y = 2$ ，则 $x^{2} y + x y^{2}$ 的值是．

查看试题解析
25. 用火柴棍拼成如下图案，其中第①个图案由4个小等边三角形围成1个小菱形，第②个图案由6个小等边三角形围成2个小菱形，……，若按此规律拼下去，则第n个图案需要火柴棍的根数为（用含n的式子表示）．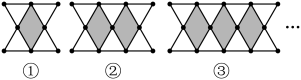

查看试题解析
26. 计算： $(- 2)^{2} + (- 2) \times 2 =$ ．

查看试题解析
27. 某天老师给同学们出了一道趣味数学题：
设有编号为1-100的100盏灯，分别对应着编号为1-100的100个开关，灯分为“亮”和“不亮”两种状态，每按一次开关改变一次相对应编号的灯的状态，所有灯的初始状态为“不亮”．现有100个人，第1个人把所有编号是1的整数倍的开关按一次，第2个人把所有编号是2的整数倍的开关按一次，第3个人把所有编号是3的整数倍的开关按一次，……，第100个人把所有编号是100的整数倍的开关按一次．问最终状态为“亮”

的灯共有多少盏？

几位同学对该问题展开了讨论：

甲：应分析每个开关被按的次数找出规律：

乙：1号开关只被第1个人按了1次，2号开关被第1个人和第2个人共按了2次，3号开关被第1个人和第3个人共按了2次，……

丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态．

根据以上同学的思维过程，可以得出最终状态为“亮”的灯共有盏．

查看试题解析
28. 新时代十年来，我国建成世界上规模最大的社会保障体系．其中基本医疗保险的参保人数由5.4亿增加到13.6亿，参保率稳定在95%．将数据13.6亿用科学记数法表示为 $1.36 \times 1 0^{n}$ 的形式，则 $n$ 的值是（备注：1亿＝100000000）．

查看试题解析

三、计算题

29. 先化简，再求值： $(\frac{2}{m - 3} + 1) \div \frac{2 m - 2}{m^{2} - 6 m + 9}$ ，然后从 $1$ ， $2$ ， $3$ ， $4$ 中选择一个合适的数代入求值．

查看试题解析
30. 先化简，再求值： $\frac{2}{x^{2} - 4} \div (1 - \frac{x}{x - 2})$ ，其中 $x = \sqrt{5} - 2$ ．

查看试题解析
31. 先化简，再求值： $\frac{a}{a^{2} - 1} - \frac{1}{a^{2} - 1}$ ，其中a=2．

查看试题解析
32.

(1)、计算： $(12 x^{4} + 6 x^{2}) \div 3 x - (- 2 x)^{2} (x + 1)$ ；

(2)、解分式方程： $\frac{5}{x^{2} + x} - \frac{1}{x^{2} - x} = 0$ ．

查看试题解析
33. 化简： $(1 - \frac{4}{a + 3}) \div \frac{a^{2} - 2 a + 1}{2 a + 6}$ ．

查看试题解析
34. 计算： $| 1 - \sqrt{2} | + {(\frac{1}{2})}^{- 2} - (π - 2023)^{0}$ ．

查看试题解析
35. 先化简，再求值： $\frac{a^{2} - 4 a + 4}{a^{2} - 4} \div \frac{a - 2}{a^{2} + 2 a} + 3$ ，其中 $a = \sqrt{3} - 3$ ．

查看试题解析

四、解答题

36. 先化简，再求值：
$(\frac{2 x - y}{x + y} - \frac{x^{2} - 2 x y + y^{2}}{x^{2} - y^{2}}) \div \frac{x - y}{x + y}$ ，其中 $x = {(\frac{1}{2})}^{- 1} ， y = (- 2023)^{0} .$

查看试题解析

五、实践探究题

37. 某数学兴趣小组运用《几何画板》软件探究y=ax²（a＞0）型抛物线图象．发现：如图1所示，该类型图象上任意一点P到定点F（0， $\frac{1}{4 a}$ ）的距离PF，始终等于它到定直线l：y= $- \frac{1}{4 a}$ 的距离PN　（该结论不需要证明）．他们称：定点F为图象的焦点，定直线l为图象的准线，y= $- \frac{1}{4 a}$ 叫做抛物线的准线方程．准线l与y轴的交点为H．其中原点O为FH的中点，FH=2OF= $\frac{1}{2 a}$ ．例如，抛物线y=2x² ，其焦点坐标为F（0， $\frac{1}{8}$ ），准线方程为l：y= $- \frac{1}{8}$ ，其中PF=PN，FH=2OF= $\frac{1}{4}$ ．

(1)、【基础训练】请分别直接写出抛物线y= $\frac{1}{4} x^{2}$ 的焦点坐标和准线l的方程：，；

(2)、【技能训练】如图2，已知抛物线y= $\frac{1}{4} x^{2}$ 上一点P（x₀ ， y₀）（x₀＞0）到焦点F的距离是它到x轴距离的3倍，求点P的坐标；

(3)、【能力提升】如图3，已知抛物线y= $\frac{1}{4} x^{2}$ 的焦点为F，准线方程为l．直线m：y= $\frac{1}{2} x - 3$ 交y轴于点C，抛物线上动点P到x轴的距离为d₁ ，到直线m的距离为d₂ ，请直接写出d₁+d₂的最小值；

(4)、【拓展延伸】该兴趣小组继续探究还发现：若将抛物线y=ax²（a＞0）平移至y=a(x-h)²+k（a＞0）．
抛物线y=a(x-h)²+k（a＞0）内有一定点F（h， $k + \frac{1}{4 a}$ ），直线l过点M（h， $k - \frac{1}{4 a}$ ）且与x轴平行．当动点P在该抛物线上运动时，点P到直线l的距离PP₁始终等于点P到点F的距离（该结论不需要证明）．例如：抛物线y=2(x-1)²+3上的动点P到点F（1， $\frac{25}{8}$ ）的距离等于点P到直线l：y= $\frac{23}{8}$ 的距离．

请阅读上面的材料，探究下题：

如图4，点D（-1， $\frac{3}{2}$ ）是第二象限内一定点，点P是抛物线y= $\frac{1}{4} x^{2}$ -1上一动点．当PO+PD取最小值时，请求出△POD的面积．

查看试题解析

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31