备战2024年中考数学细点逐一突破真题训练第5章不等式（组）及其应用（2）-在线组卷题库

1. 如图，数轴上的点 $A ， B$ 表示的数分别是 $a ， b$ ．如果 $| a | < | b |$ ，且 $a b < 0$ ，那么该数轴的原点 $O$ 的位置应该在（）

A、点 $A$ 的左侧 B、点 $B$ 的右侧 C、点 $A$ 与点 $B$ 之间且靠近点 $A$ D、点 $A$ 与点 $B$ 之间且靠近点 $B$

查看试题解析
2. 已知关于x的不等式（a﹣1）x＞2的解集为 $x < \frac{2}{a - 1}$ ，则a的取值范围是（）

A、a＜1 B、a＞1 C、a＜0 D、a＞0

查看试题解析
3. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
4. 已知 $b > a > 0$ ，下列选项正确的是（）

A、 $\frac{a}{b} < \frac{a - 1}{b - 1}$ B、 $\frac{a}{b} < \frac{a + 1}{b + 1}$ C、 $\frac{1}{a^{2} - 1} < \frac{1}{{(a - 1)}^{2}}$ D、 $\frac{a}{b} < \frac{a + m}{b + m}$

查看试题解析
5. 已知实数 $a$ ， $b$ ， $c$ 满足 $a - 3 b + c = 0$ ， $a + 3 b + c < 0$ ，则下列选项中正确的（）

A、 $b < 0$ ， $b^{2} - \frac{4}{9} a c \leq 0$ B、 $b < 0$ ， $b^{2} - \frac{4}{9} a c \geq 0$ C、 $b > 0$ ， $b^{2} - \frac{4}{9} a c \leq 0$ D、 $b > 0$ ， $b^{2} - \frac{4}{9} a c \geq 0$

查看试题解析

6. 疫情期间，有一批患者要入住邵阳市中心医院的某栋大楼，若每间住4人，则有38人无法入住；若每间住5人，则最后一间没住满．若设房间数为x间，则可列不等式组为：．

查看试题解析
7. 解不等式（组）：

(1)、 $\frac{2 x - 1}{3} \leq 5$

(2)、 ${\begin{array}{l} 5 x - 2 > 2 x - 8 \\ 1 - 2 x \geq - 3 \end{array}$

查看试题解析
8. 已知关于x的不等式组 ${\begin{cases} x - a \geq 0 \\ 3 - 2 x > 0 \end{cases}$ 的整数解共有4个，则a的取值范围是（）

A、﹣3＜a≤﹣2 B、﹣3≤a＜﹣2 C、﹣3＜a＜﹣2 D、a＜﹣2

查看试题解析
9. 已知不等式组 ${\begin{cases} x - a > 2 \\ x + 1 < b \end{cases}$ 的解集是 $- 1 ＜ x ＜ 1$ ，则 $(a + b)^{2023}$ =（）

A、0 B、-1 C、1 D、2023

查看试题解析
10. 用锤子以相同的力将铁钉垂直钉入木块，随着铁钉的深入，铁钉所受的阻力也越来越大．当铁钉未进入木块部分长度足够时，每次钉入木块的铁钉长度是前一次的 $\frac{1}{3}$ ，已知这个铁钉被敲击3次后全部进入木块（木块足够厚），且第一次敲击后，铁钉进入木块的长度是acm，若铁钉总长度为6cm，则a的取值范围是．

查看试题解析
11. 若整数 $a$ 使得关于 $x$ 的不等式组 ${\begin{array}{l} 3 x - 2 (x - 1) > 3 \\ \frac{1 - x}{2} \geq 3 - a \end{array}$ 有解，且使得关于 $x$ 的分式方程 $2 + \frac{a}{x - 4} = \frac{10 - x}{x - 4}$ 有正整数解，那么符合条件的所有整数 $a$ 的和为．

查看试题解析
12. 对于三个数a ， b ， c ，我们规定 $m a x {a ， b ， c}$ 表示这三个数中最大的数.例如 $m a x {1 ， 2 ， - 3} = 2$ ， $m a x {- 2 ， 4 ， 4} = 4$ 若 $m a x {1 ， x + 1 ， 2 x} = 2 x$ ，则x的取值范围是．

查看试题解析

13. 不等式 $6 - 2 x \geq 3 x - 4$ 的正整数解有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
14. 若关于x的分式方程 $\frac{x}{x - 1} + 1 = \frac{m}{1 - x}$ 的解为非负数，则m的取值范围是（）

A、 $m \leq 1$ 且 $m \neq - 1$ B、 $m \geq - 1$ 且 $m \neq 1$ C、 $m < 1$ 且 $m \neq - 1$ D、 $m > - 1$ 且 $m \neq 1$

查看试题解析
15. 若不等式组 ${\begin{array}{l} 1 + x > a \\ 2 x - 4 \leq 0 \end{array}$ 有解，则 $a$ 的取值范围是（）

A、 $a ⩽ 3$ B、 $a < 3$ C、 $a < 2$ D、 $a ⩽ 2$

查看试题解析
16. 若整数 $a$ 使得关于 $x$ 的分式方程 $\frac{3}{x (x - 1)} - \frac{1}{x} = \frac{a}{2 (x - 1)}$ 有正整数解，且使关于 $y$ 的不等式组 $\{\begin{array}{l} 4 (y - 1) > 3 (y - 2) + 1 \\ \frac{1 - y}{2} \geq - a - 1 \end{array}$ 至少有 $4$ 个整数解，那么符合条件的所有整数 $a$ 的和为（）

A、 $- 1$ B、 $1$ C、 $2$ D、 $8$

查看试题解析
17. 关于x，y的方程组 ${\begin{array}{l} 2 x - y = 3 k - 1 \\ x - 2 y = k \end{array}$ 的解中，x与y的和不大于3，则k的取值范围是（）

A、 $k \geq 2$ B、 $k \leq 2$ C、 $k \geq 1$ D、 $k \leq 1$

查看试题解析
18. 若关于x的不等式组 $\{\begin{matrix} \frac{x + 2}{3} > \frac{x}{2} + 1 ， \\ 4 x + a < x - 1 \end{matrix}$ 的解为x<-2，且关于y的分式方程 $\frac{a + 2}{y - 1} + \frac{y + 2}{1 - y} = 2$ 的解为正数，则所有满足条件的整数a的值之和为.

查看试题解析

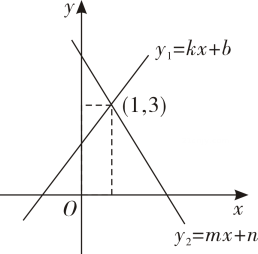
19. 如图，一次函数y₁＝kx+b与y₂＝mx+n的图象相交于点（1，3），则方程组 ${\begin{cases} y_{1} = k x + b \\ y_{2} = m x + n \end{cases}$ 的解为 ${\begin{cases} x = 1 \\ y = 3 \end{cases}$ ，关于x的不等式kx+b＞mx+n的解为．

查看试题解析
20. 如图，已知二次函数y₁₌ $a x^{2} + b x + c (a \neq 0)$ 的图象与正比例函数y₂＝kx（k≠0）的图象相交于点A（3，4），与x轴交于点B（2，0），若0＜y₁＜y₂ ，则x的取值范围是（　　）

A、 $- \frac{2}{3} < x < 3$ B、2＜x＜3 C、 $- \frac{2}{3} < x < 2$ D、0＜x＜3

查看试题解析
21. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象与 $y = - 2 x$ 的图象交于点 $(m ， - 4)$ ．则对于不等式 $\underset{˙}{k} \underset{˙}{x} \underset{˙}{-} \underset{˙}{b} < - 2 x$ ，下列说法正确的是（）

A、当 $k < - 2$ 时， $x > 2$ B、当 $k < - 2$ 时， $x < 2$ C、当 $k > - 2$ 且 $k \neq 0$ 时， $x > - 2$ D、当 $k > - 2$ 且 $k \neq 0$ 时， $x < - 2$

查看试题解析
22. 已知反比例函数 $y = \frac{k}{x}$ 的图像经过点 $(- 1 ， 4)$ ．

(1)、求 $k$ 的值；

(2)、完成下面的解答过程．
解不等式组 ${\begin{array}{l} x + 3 > 1 ① \\ \frac{k}{x} > 1 ② \end{array}$

解：解不等式①，得；

在方格中画出反比例函数 $y = \frac{k}{x}$ 的大致图像，根据图像写出不等式②的解集是；

把不等式①和②的解集在数轴上表示出来；

从图中可以找出这两个不等式解集的公共部分，得到原不等式组的解集是．

查看试题解析
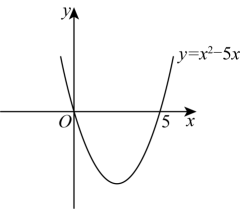
23. 自主学习，请阅读下列解题过程．
解一元二次不等式： $x^{2} - 5 x$ ＞0．
解：设 $x^{2} - 5 x$ =0，解得： $x_{1}$ =0， $x_{2}$ =5，则抛物线y= $x^{2} - 5 x$ 与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y= $x^{2} - 5 x$ 的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即 $x^{2} - 5 x$ ＞0，所以，一元二次不等式 $x^{2} - 5 x$ ＞0的解集为：x＜0或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：

(1)、上述解题过程中，渗透了下列数学思想中的和．（只填序号）
①转化思想 ②分类讨论思想 ③数形结合思想

(2)、一元二次不等式 $x^{2} - 5 x$ ＜0的解集为．

(3)、用类似的方法解一元二次不等式： $x^{2} - 2 x - 3$ ＞0．

查看试题解析

24. 综合与实践问题情境：“文房四宝”是中国独有的书法绘画工具，即笔、墨、纸、砚，文房四宝之名，起源于南北朝时期．某中学为了落实双减政策，丰富学生的课后服务活动，开设了书法社团，计划为学生购买A，B两种型号“文房四宝”共40套．已知某文化用品店每套A型号的“文房四宝”的标价比B型号的“文房四宝”的标价高30%，若按标价购买需花费4300元，其中购买B型号“文房四宝”花费3000元．
问题解决：

(1)、求每套B型号的“文房四宝”的标价．

(2)、若经过与店主协商，考虑到购买较多，店主同意该中学按A型号“文房四宝”九折，B型号“文房四宝”八折的优惠价购入，则购买原定数量的A，B型号“文房四宝”共需花费多少元？

(3)、一段时间后，由于传统文化广受关注，另一所学校想要购入A，B两种型号“文房四宝”共100套。店主继续以（2）中的折扣价进行销售，已知A，B两种型号的“文房四宝”每套进价分别为67元和50元，若通过此单生意，该店主获利不低于3800元，则该校在这家店至少买了套A型“文房四宝”？

查看试题解析
25. 某企业有甲、乙两个车间用于生产医用防护服.甲车间每天生产的数量是乙车间每天生产数量的1.5倍，两车间各加工6000套医用防护服，甲车间比乙车间少用4天.

(1)、甲、乙两车间每天各生产多少套医用防护服？

(2)、已知甲、乙两车间生产这种医用防护服每天的生产费用分别是12000元和10000元，现有18000套医用防护服的生产任务，甲车间单独生产一段时间后另有安排，剩余任务由乙车间单独完成.如果总生产费用不超过339000元，则甲车间至少需要生产几天？

查看试题解析
26. 某公园要铺设广场地面，其图案设计如图所示．矩形地面的长为50米，宽为32米，中心建设一个直径为10米的圆形喷泉，四周各角留一个相同的矩形花坛，图中阴影处铺设地砖．已知矩形花坛的长比宽多15米，铺设地砖的面积是1125平方米．（ $π$ 取3）

(1)、求矩形花坛的宽是多少米；

(2)、四个角的矩形花坛由甲、乙两个工程队负责绿化种植，甲工程队每平方米施工费为100元，乙工程队每平方米施工费为120元．若完成此工程的工程款不超过42000元，至少要安排甲队施工多少平方米？

查看试题解析

27. 【综合与实践】
学校在某商场购买甲、乙两种不同类型的足球，相关信息如下：购买甲种足球共用2000元，购买乙种足球共花费1400元.已知购买一个乙种足球比购买一个甲种足球多花20元.设购买一个甲种足球的单价是 $x$ 元。

(1)、请用含 $x$ 的代数式分别表示购买甲、乙两种足球的数量；

(2)、若本次购买甲种足球的数量是购买乙种足球数量的2倍，求甲、乙两种足球在此商场的销售单价；

(3)、为满足学生需求，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的销售单价进行调整，甲种足球的销售单价比上次购买时提高了10％，乙种足球的销售单价比上次购买时降低了10％.如果此次购买甲、乙两种足球的总费用不超过2950元，求这所学校最多可以购买乙种足球的数量.

查看试题解析
28. 某商场“双 $11$ ”前准备从供货商家处新选购一批商品，已知按进价购进 $1$ 件甲种商品和 $2$ 件乙种商品共需 $320$ 元，购进 $3$ 件甲种商品和 $2$ 件乙种商品共需 $520$ 元．

(1)、求甲、乙两种商品每件的进价分别是多少元？

(2)、若甲种商品的售价为每件 $120$ 元，乙种商品的售价为每件 $140$ 元，该商场准备购进甲、乙两种商品共 $50$ 件，且这两种商品全部售出后总利润不少于 $1350$ 元，不高于 $1375$ 元．若购进甲种商品 $m$ 件，请问该商场共有哪几种进货方案？

(3)、根据往年销售情况，商场计划在“双 $11$ ”当天将现有的甲、乙两种商品共 $46$ 件按 $(2)$ 中的售价全部售完．但因受拉尼娜现象形成的冷空气持续影响，当天出现的雨雪天气使得 $46$ 件商品没有全部售完，两种商品的实际销售利润总和为 $1220$ 元．那么，“双 $11$ ”当天商场至少卖出乙种商品多少件？

查看试题解析

29. 为了迎接“十·一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：

运动鞋价格/种类	甲	乙
进价（元/双）	m	$m - 20$
售价（元/双）	160	120

已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．

(1)、求m的值；

(2)、要使购进的甲、乙两种运动鞋共200双的总利润（利润

=

售价

-

进价）不少于10800元，且不超过11100元，问该专卖店有几种进货方案？

(3)、在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠

a (10 < a < 35)

元出售．乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？

查看试题解析

30. 观察： $\frac{1}{2} < \frac{1 + 1}{2 + 1}$ ， $\frac{1}{3} < \frac{1 + 1}{3 + 1}$ ， $\frac{3}{4} < \frac{3 + 1}{4 + 1}$ ， $\frac{4}{7} < \frac{4 + 1}{7 + 1}$ ．

(1)、猜想：当 $0 < b < a$ 时， $\frac{b}{a}$ $\frac{b + 1}{a + 1}$ ， $\frac{b}{a}$ $y = 1$ ， $\frac{b}{a}$ $\frac{b + 3}{a + 3}$ （“>”“＝”“<”填空）

(2)、探究：当 $0 < b < a$ 时， $\frac{b}{a}$ 与 $\frac{b + n}{a + n}$ （其中n为正整数）的大小关系，并说明理由．

查看试题解析
31. 对于“已知 $x + y = 1$ ，求 $x y$ 的最大值”这个问题，小明是这样求解的：
∵ $x + y = 1$ ， ∴ $y = 1 - x$ ， ∴ $x y = x (1 - x) = x - x^{2} = - {(x - \frac{1}{2})}^{2} + \frac{1}{4}$
∴ $x y \leq \frac{1}{4}$ ，所以 $x y$ 的最大值为 $\frac{1}{4}$ .
请你按照这种方法计算：当 $2 n + m = 4 (m > 0 ， n > 0)$ 时， $\frac{2}{m} + \frac{1}{n}$ 的最小值.

查看试题解析

备战2024年中考数学细点逐一突破真题训练第5章不等式（组）及其应用（2）

一、不等式性质

二、不等式（组）及其解集

三、不等式（组）的特殊解

四、函数与不等式结合

五、一次不等式的实际应用

六、方程组与不等式结合

七、实践探究题