2023-2024学年春季期苏科版七下第八章单元测试

试卷更新日期：2024-03-04 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共15分）

1. 下列运算中，正确的是（）

A、 $3 a^{2} - a^{2} = 2$ B、 ${(2 a^{2})}^{2} = 2 a^{4}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 $a^{3} \cdot a^{2} = a^{5}$

查看试题解析
2. 有下列各式：①( $\frac{1}{4}$ )^-2=16；②a²·a²=2a²；③(-3a²)³=-9a⁵；④a⁵+a³=a⁸；⑤(2-π)⁰=1；⑥m⁶÷m²=m⁴ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 计算(6×10³)·(8×10⁵)的结果为（）

A、48×10¹⁵ B、48×10⁹ C、4.8×10¹⁵ D、4.8×10⁹

查看试题解析
4. 已知m，n是正整数，且2^m·2ⁿ=2⁵ ，则m，n的值共有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
5. 已知 $2^{a} = 5$ ， $4^{b} = 7$ ，则 $2^{a + 2 b}$ 的值是（　　）

A、 $35$ B、 $19$ C、 $12$ D、 $10$

查看试题解析
6. 已知a=8³³ ， b=16²⁵ ， c=32¹⁹ ，则有（）

A、a<b<c B、c<b<a C、c<a<b D、a<c<b

查看试题解析
7. 当x=-6，y= $\frac{1}{6}$ 时，x²⁰¹⁸y²⁰¹⁹的值为（）

A、 $\frac{1}{6}$ B、- $\frac{1}{6}$ C、6 D、-6

查看试题解析
8. 若 $3^{x} + 3^{x} + 3^{x} + 3^{x} = \frac{4}{9}$ ，则 $x =$ （）

A、-2 B、-1 C、0 D、 $\frac{1}{4}$

查看试题解析
9. 19⁹³+93¹⁹的个位数字是（　）

A、2 B、4 C、6 D、8

查看试题解析
10. 如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．下列判断正确的是（）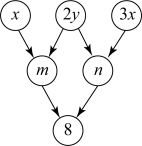

结论 Ⅰ ：若n的值为5，则y的值为1；

结论Ⅱ： $x + y$ 的值为定值；

结论Ⅲ：若 $x^{m - 3 n} = 1$ ，则y的值为4或1．

A、Ⅰ ，Ⅲ均对 B、Ⅱ对，Ⅲ错 C、Ⅱ错，Ⅲ对 D、Ⅰ ，Ⅱ均错

查看试题解析

二、填空题（第11-15题每题1分，第16-24题每题2分）

11. 已知 $a^{m} = 5$ ， $a^{n} = 10$ ，则 $a^{m - n} =$ ．

查看试题解析
12. 计算 ${(- 2)}^{3} \times {(\frac{1}{2})}^{1} =$ .

查看试题解析
13. 有一种冠状病毒直径为 0.000 000 012 米，数0 000 000 012用科学记数法表示为

查看试题解析
14. 有下列运算：① ${(- x^{2})}^{3} = - x^{5} ； ② 3 x y - 3 y x = 0 ；$ $③ 3^{1 \infty} \times {(- 3)}^{100} = 0 ， ④ m \cdot m^{5} \cdot m^{7} = m^{12} ，$ $⑤ 3 a^{4} + a^{4} = 3 a^{8} ， ⑥ {(x^{2})}^{4} = x^{16} .$ .其中正确的是（填序号）.

查看试题解析
15. 计算： $(- x^{2}) \cdot {(- x)}^{2} \cdot {(- x)}^{3} =_{.}$

查看试题解析
16. 比较 ${(\frac{1}{6})}^{- 1} ， {(- 2)}^{0} ， {(- 3)}^{2}$ 这三个数的大小，并用“<”号连接：

查看试题解析
17. 如果a，b，c满足2^a=3，2^b=5，2^c=135，那么a，b，c满足的等式为.

查看试题解析
18. 若5x-3y-2=0，则 $10^{5 x} \div 10^{3 y} =$ .

查看试题解析
19. 已知3^x+1·5^x+1=15^2x-1 ，则x= ．

查看试题解析
20. 若 ${(5 - 2 x)}^{x + 1} = 1$ ，则 $x =$ ．

查看试题解析
21. 已知2×8^m×16^m=2²² ，则(-m²)⁴÷(m³·m²)的值为.

查看试题解析
22. 计算 ${(27)}^{- \frac{1}{3}} =$ ．

查看试题解析
23. 已知整数a，b满足（ $\frac{2}{9}$ ）^a•（ $\frac{3}{4}$ ）^b=8，则a﹣b= ．

查看试题解析
24. 已知 ${(x - 2)}^{x^{2} - 4}$ = 1，则 x =（）

查看试题解析

三、计算题（共6题，共39分）

25. 计算：

(1)、 $b^{2} \cdot b^{3} \div b^{5}$

(2)、 $- 3 + 2^{0} - {(\frac{1}{2})}^{- 1}$

查看试题解析
26. 计算：

(1)、(-t⁴)³+(-t²)⁶ ．

(2)、(m⁴)²+(m³)²-m(m²)²·m³ ．

(3)、x^n-1·(xⁿ⁺²)²·x²·(x^2n-1)³ ．

(4)、(x-y)³·(y-x)²^·(x-y)⁴ ．

查看试题解析
27. 计算下列各式，结果用幂的形式表示．

(1)、 (-14)³×14．

(2)、 (a-b) ·(b-a)⁵

(3)、 (-5)²×(-5)³×54．

(4)、 10 000 000×(-10 000 000 000)

(5)、 (-2)²⁰²⁰+(- 2)²⁰²¹ ．

(6)、 1000×10^m+1 ．

查看试题解析
28. 计算：

(1)、 2³×2³+2×2⁴ ．

(2)、 x⁵·x³-x⁴x⁴+x⁷·x+x⁶·x²

(3)、已知a^x=2，a^y=3，求下列两式的值：
①a^x+y ．
②a^2x+3y ．

查看试题解析
29. 计算：

(1)、 (xⁿ)²·x^m^-n ．

(2)、 (a)²-(-a)²·(-2a²)³ ．

(3)、 (-2a⁴)³+a⁶·a⁶ ．

(4)、 x²·(-2x)⁴-(-3x³)²+(-x²)³ ．

(5)、 [2(a-b)²]³·[(b- a)³]⁵(可保留(a- b)的形式)

查看试题解析
30.

(1)、已知5^m=6，7ⁿ=8，求35^2m的值．

(2)、已知2^x+33^x+3=36^x-2 ，求x的值．

(3)、已知3m+2n=8，求8^m·4ⁿ的值．

查看试题解析

四、解答题（共3题，共23分）

31. 已知n为正整数，且x²ⁿ=4

(1)、求x^n-3·x³⁽ⁿ⁺¹⁾的值；

(2)、求9(x³ⁿ)²-13(x²)²ⁿ的值．

查看试题解析
32. 计算：

(1)、已知a^m=2，aⁿ=4，a^k=32，求a^3m+2n-k的值．

(2)、已知x^m=5，x^m+n=125，求x^2m-n的值．

(3)、已知9^m÷3^2m+2=( $\frac{1}{3}$ )ⁿ ，求n的值．

(4)、已知4×16^m×64^m=4²¹ ，则(-m²)³÷(m³·m²)的值.

查看试题解析
33. 已知16^m=4×2²ⁿ^﹣² ， 27ⁿ=9×3^m⁺³ ，求（n﹣m）²⁰¹⁰的值．

查看试题解析