初中数学同步训练必刷培优卷（北师大版七年级下册1.7整式的除法）

试卷更新日期：2024-03-04 类型：同步测试

进入出卷网下载

一、选择题

1. 计算（x+3y）²-（3x+y）²的结果是（）

A、8x²-8y² B、8y²-8x² C、8（x+y）² D、8（x-y）²

查看试题解析
2. 若 ${(x + 2 y)}^{2} = {(x - 2 y)}^{2} + A ，$ 则A等于（）

A、8xy B、-8xy C、8y² D、4xy

查看试题解析
3. 下列运算不正确的是（）

A、 $\frac{3}{4} x^{3} \div \frac{4}{3} x^{2} = \frac{9}{16} x$ B、(-2³x²y)÷(-3²xy)= $\frac{8}{9}$ x C、6a²bc÷(-6c)=-a²b D、-x³y³÷y³=-x³y

查看试题解析
4. 设a，b是实数，定义新运算“*”：a*b=（a+b）² ，给出下列结论：
①若a*b=0，则a=0且b=0.②a*b=b*a.③a*（b+c）=a*b+a*c.④a*b=（-a）*（-b）.
其中正确的是（）

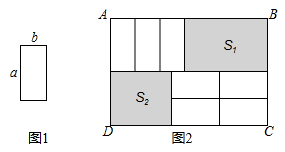
A、①③ B、②④ C、①②③ D、②③④

查看试题解析
5. 在长方形ABCD内，将两张边长分别为a和b（a>b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，若图1中阴影部分的面积为 S₁，图2中阴影部分的面积和为 S₂，则关于 S₁，S₂的大小关系表述正确的是（）

A、 $S_{1} > S_{2}$ B、 $S_{1} < S_{2}$ C、 $S_{1} = S_{2}$ D、 $S_{1} \geq S_{2}$

查看试题解析
6. 若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为40；其中5个如图2摆放，构造出一个长方形，其中阴影部分面积为100（各个小长方形之间不重叠不留空），则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析
7. 如图，大正方形的边长为 $m$ ，小正方形的边长为 $n$ ， $x$ ， $y$ 表示四个相同长方形的两边长（ $x > y$ ）.则① $x - y = n$ ；② $x y = \frac{m^{2} - n^{2}}{4}$ ；③ $x^{2} - y^{2} = m n$ ；④ $x^{2} + y^{2} = \frac{m^{2} - n^{2}}{2}$ ，中正确的是（）

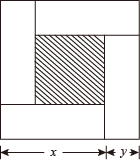A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
8. 某公司有如图所示的甲、乙、丙、丁四个生产基地．现决定在其中一个基地修建总仓库，以方便公司对各基地生产的产品进行集中存储．已知甲、乙、丙、丁各基地的产量之比等于4：5：4：2，各基地之间的距离之比a：b：c：d：e＝2：3：4：3：3（因条件限制，只有图示中的五条运输渠道），当产品的运输数量和运输路程均相等时，所需的运费相等．若要使总运费最低，则修建总仓库的最佳位置为（）

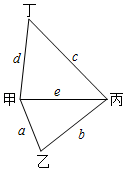A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

9. 已知A=3a，B是多项式，在计算 B÷A时，小虎同学把B÷A看成了B+A，结果得9a² ，则B÷A =.

查看试题解析
10. 有一块绿地的形状如图，则它的面积为.

查看试题解析
11. 若一个四位正整数（各个数位均不为0），百位数字比千位数字小3，个位数字比十位数字小2，则称该数为“和平数”，例如：4131，9642都是“和平数”，将一个四位正整数 $P$ 的百位和十位交换位置后得到四位数 $Q ， G (P) = \frac{P - Q}{90}$ ，若 $P$ 为“和平数”，且 $P$ 能被9整除，则满足条件的所有 $P$ 值中， $G (P)$ 的最大值是．

查看试题解析

三、综合题

12. 如图，长为40，宽为x的大长方形被分割为9小块，除阴影A， B两块外，其余7块是形状、大小完全相同的小长方形，其较短一边长为y．

(1)、分别用含x，y的代数式表示阴影A，B两块的周长，并计算阴影A，B两块的周长和．

(2)、分别用含x，y的代数式表示阴影A，B两块的面积，并计算阴影A，B的面积差．

(3)、当y取何值时，阴影A与阴影B的面积差不会随着x的变化而变化，并求出这个值．

查看试题解析
13. 7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按如图2、3的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．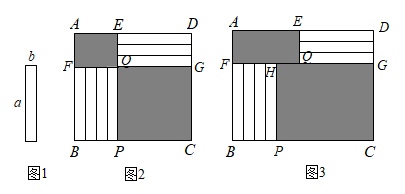

(1)、如图2，点E、Q、P在同一直线上，点F、Q、G在同一直线上，右下角与左上角的阴影部分的面积的差为（用含a、b的代数式表示），矩形ABCD的面积为（用含a、b的代数式表示）；

(2)、如图3，点F、H、Q、G在同一直线上，设右下角与左上角的阴影部分的面积的差为S，PC＝x．当BC的长度变化时，按照同样的放置方式，S始终保持不变，那么a、b必须满足什么条件？

查看试题解析
14. （知识回顾）
七年级学习代数式求值时，遇到这样一类题“代数式 $a x - y + 6 + 3 x - 5 y - 1$ 的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式= $(a + 3) x - 6 y + 5$ ，所以 $a + 3 = 0$ ，则 $a = - 3$ .

(1)、（理解应用）
若关于x的多项式 $(2 x - 3) m + 2 m^{2} - 3 x$ 的值与x的取值无关，求m值；

(2)、已知 $A = (2 x + 1) (x - 1) - x (1 - 3 y)$ ， $B = - x^{2} + x y - 1$ ，且3A+6B的值与x无关，求y的值；

(3)、（能力提升）
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分(图中阴影部分)，设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求a与b的等量关系.

查看试题解析