初中数学同步训练必刷培优卷(北师大版七年级下册1.4整式的乘法)
试卷更新日期:2024-03-04 类型:同步测试
一、选择题
-
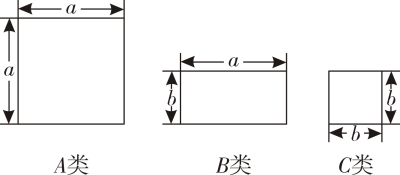
1. 已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )A、-3 B、-1 C、1 D、52. 计算(2x-1)(1-2x)的结果是( )A、 B、 C、 D、3. 下列计算中,正确的是( )A、a4⋅a3=a¹2 B、5a(b-3a2)=5ab-15a3 C、(a+b)(a-2b)=a2-2b2 D、(x-1)(x2+2)=x3+2x-24. 若(x-3)(2x+m)=2x2+nx-15,则( )A、m=-5,n=1 B、m=5,n=-1 C、m=-5,n=-1 D、m=5,n=15. 若(x﹣4)(x+8)=x2+mx﹣n,则m、n的值分别是( )A、4,32 B、4,﹣32 C、﹣4,32 D、﹣4,﹣326. 若p=x2y,则计算-x10y5(-2x2y)3的结果为( )A、-8p8 B、8p8 C、-6p8 D、6p87. 如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(2a+3b),宽为(a+2b)的大长方形,则需要A类、B类和C类卡片的张数分别为( )
 A、 , , B、 , , C、 , , D、 , ,8. 如图,四位同学给出了四种表示该长方形面积的多项式,
A、 , , B、 , , C、 , , D、 , ,8. 如图,四位同学给出了四种表示该长方形面积的多项式,

①
②
③
④
你认为其中正确的有( )
A、①② B、③④ C、①②③ D、①②③④二、填空题
-
9. 已知多项式(x-a)与(x2+2x-1)的乘积中不含x2项,则常数a的值是 .10. 如图所示的正方形和长方形卡片各有若干张,若要拼成一个长为(2a+b),宽为(a+ b)的长方形,则需要A类卡片张,B类卡片张,C类卡片张.
 11. 要使(x3+ax2-x)(-8x4)的运算结果中不含x6的项,则a的值为.12. 如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有种.
11. 要使(x3+ax2-x)(-8x4)的运算结果中不含x6的项,则a的值为.12. 如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有种.
三、计算题
-
13.(1)、若3m=6,3n=2,求32m-3n+1的值.(2)、已知x2-3x-1=0,求代数式(x-1)(3x+1)-(x+2)2+5的值.
四、解答题
-
14. 计算:(a-b)2m-1·(b-a)2m·(a-b)2m+1 , 其中m为正整数.15. 教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作:
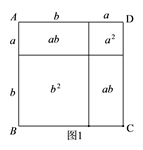
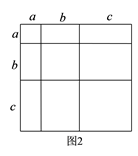
(1)把它看成是一个大正方形,则它的面积为 ;
(2)把它看成是2个小长方形和2个小正方形组成的,则它的面积为 ;因此,可得到等式: .① 类比教材中的方法,由图2中的大正方形可得等式: .
② 试在图2右边空白处画出面积为 的长方形的示意图(标注好a、b),由图形可知,多项式 可分解因式为: .
在上方空白处画出②中的示意图
③ 若将代数式 展开后合并同类项,得到多项式N,则多项式N的项数一共有 项.
-