备考2024年中考数学核心素养专题四数与式的阅读理解

试卷更新日期：2024-03-03 类型：二轮复习

进入出卷网下载

一、选择题

1. 阅读材料：对于任何实数，我们规定符号 $| \begin{matrix} a \\ c \end{matrix}$ $\begin{matrix} b \\ d \end{matrix} |$ 的意义是 $| \begin{matrix} a \\ c \end{matrix}$ $\begin{matrix} b \\ d \end{matrix} |$ =ad-bc．按照这个规定，若 $| \begin{matrix} x - 2 \\ 2 x - 1 \end{matrix}$ $\begin{matrix} x \\ x - 2 \end{matrix} |$ ＝0，则x的值是（）

A、－4 B、1 C、－4或1 D、不存在

查看试题解析
2. 阅读材料：在处理分数和分式的问题时，有时由于分子大于分母，或分子的次数高于分母的次数，在实际运算时难度较大，这时，我们可将分数（分式）拆分成一个整数（整式）与一个真分数（真分式）的和（差）的形式，通过对它的简单分析来解决问题，我们称这种方法为分离常数法，此法在处理分式或整除问题时颇为有效.将分式分离常数可类比假分数变形带分数的方法进行.如： $\frac{a^{2} - 2 a + 3}{a - 1} = \frac{a (a - 1) + a - 2 a + 3}{a - 1} = a + \frac{- (a - 1) + 2}{a - 1} =$ a-1 $+ \frac{2}{a - 1}$ ，这样，分式就拆分成一个分式 $\frac{2}{a - 1}$ 与一个整式a-1的和的形式，下列说法正确的有（）个.
①若x为整数， $\frac{x + 4}{x + 2}$ 为负整数，则x＝-3；②6 $＜ \frac{6 x^{2} + 18}{x^{2} + 2} \leq$ 9；③若分式 $\frac{5 x^{2} + 9 x - 3}{x + 2}$ 拆分成一个整式与一个真分式（分子为整数）的和（差）的形式为：5m-11 $+ \frac{1}{n - 6}$ （整式部分对应等于5m-11，真分式部分对应等于 $\frac{1}{n - 6}$ ），则m²+n²+mn的最小值为27.

A、0 B、1 C、2 D、3

查看试题解析
3. 在平面直角坐标系xOy中，点P（x₀ ， y₀）到直线Ax+By+C＝0的距离公式为d＝ $\frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ，例如：点P₀（0，0）到直线4x+3y﹣3＝0的距离为d＝ $\frac{| 4 \times 0 + 3 \times 0 - 3 |}{\sqrt{4^{2} + 3^{2}}}$ ＝ $\frac{3}{5}$ ，根据以上材料，求点P₁（3，4）到直线y＝﹣ $\frac{3}{4}$ x+ $\frac{5}{4}$ 的距离为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 阅读材料：坐标平面内，对于抛物线y=ax²+bx（a≠0），我们把点（ $- \frac{b}{2 a}$ ， $\frac{1 - b^{2}}{4 a}$ ）称为该抛物线的焦点，把y= $- \frac{b^{2} + 1}{4 a}$ 称为该抛物线的准线方程。例如：抛物线y=x²+2x的焦点为（-1， $- \frac{3}{4}$ ），准线方程是y= $- \frac{5}{4}$ 。根据材料，现已知抛物线y=ax²+bx（a≠0）的焦点的纵坐标为3，准线方程y=5，则关于二次函数y=ax²+bx的最值情况，下列说法正确的是（）

A、最大值为4 B、最小值为4 C、最大值为3.5 D、最小值为3.5

查看试题解析

二、填空题

5. 阅读材料：希腊几何学家海伦和我国南宋数学家秦九韶曾提出利用三角形的三边求面积的公式，称为海伦—秦九韶公式：如果一个三角形的三边长分别是 $a$ ， $b$ ， $c$ ，记 $p = \frac{a + b + c}{2}$ ，那么三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ．如图，在 $△ A B C$ 中， $a = 7$ ， $b = 5$ ， $c = 6$ ，则 $B C$ 边上的高为．

查看试题解析
6. 读一读：式子“ $1 + 2 + 3 + 4 + \dots + 100$ ”表示从 $1$ 开始的 $100$ 个连续自然数的和，由于式子比较长，书写不方便，为了简便起见，我们将其表示为 $\sum_{n = 1}^{100} n$ ，这里“ $\sum$ ”是求和符号，通过对以上材料的阅读，计算 $\sum_{n = 1}^{2016} \frac{1}{n (n + 1)} =$ ．

查看试题解析
7. 阅读材料：整体代值是数学中常用的方法.例如“已知 $3 a - b = 2$ ，求代数式 $6 a - 2 b - 1$ 的值.”可以这样解： $6 a - 2 b - 1 = 2 (3 a - b) - 1 = 2 \times 2 - 1 = 3$ .根据阅读材料，解决问题：若 $x = 2$ 是关于x的一元一次方程 $a x + b = 3$ 的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看试题解析
8. 阅读材料：写出二元一次方程x﹣3y=6的几个解： ${\begin{matrix} x = 0 \\ y = - 2 \end{matrix}$ ， ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ ， ${\begin{matrix} x = 6 \\ y = 0 \end{matrix}$ ，…，发现这些解的一般形式可表示为 ${\begin{matrix} x = 3 m \\ y = m - 2 \end{matrix}$ （m为有理数）．把一般形式再变形为 ${\begin{matrix} m = \frac{x}{3} \\ m = y + 2 \end{matrix}$ ，可得 $\frac{x}{3}$ =y+2，整理得原方程x﹣3y=6．根据阅读材料解答下列问题：若二元一次方程ax+by=c的解，可以写成 ${\begin{matrix} x = 2 n \\ y = n + 1 \end{matrix}$ （n为有理数），则a+b+c= ．

查看试题解析
9. 自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如: $\frac{x - 2}{x + 1}$ >0; $\frac{2 x + 3}{x - 1}$ <0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
①若a>0,b>0,则 $\frac{a}{b}$ >0;若a<0,b<0,则 $\frac{a}{b}$ >0;
②若a>0,b<0,则 $\frac{a}{b}$ <0;若a<0,b>0,则 $\frac{a}{b}$ <0.
反之①若 $\frac{a}{b}$ >0,则 ${\begin{matrix} a > 0 \\ b > 0 \end{matrix}$ 或 ${\begin{matrix} a < 0 \\ b < 0 \end{matrix}$
②若 $\frac{a}{b}$ <0,则或.
根据上述规律,求不等式 $\frac{x - 2}{x + 1}$ >0的解集.

查看试题解析
10. 阅读下面材料：小明想探究函数 $y = \sqrt{x^{2} - 1}$ 的性质，他借助计算器求出了y与x的几组对应值，并在平面直角坐标系中画出了函数图象：
x
…
－3
－2
－1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…
小聪看了一眼就说：“你画的图象肯定是错误的．”
请回答：
①小聪判断的理由是．
②当 $y = 0$ 时，x的值为．
③请写出函数 $y = \sqrt{x^{2} - 1}$ 的一条性质：．

查看试题解析
11. 阅读下面材料：在数学课上，老师给同学们布置了一道尺规作图题：
尺规作图：作Rt△ABC，使其斜边AB=c，一条直角边BC=a．已知：如图1，正比例函数和反比例函数的
图象分别交于M、N两点．
要求：在y轴上求作点P，使得∠MPN为直角．
小丽的作法如下：如图2，以点O为圆心，以OM长为半径作⊙O，
⊙O与y轴交于P₁、P₂两点，则点P₁、P₂即为所求．
老师说：“小丽的作法正确．”
请回答：小丽这样作图的依据是

查看试题解析

三、实践探究题

12. 认真阅读下面的材料，完成有关问题.
材料：在学习绝对值时，我们知道了绝对值的几何意义，如 $| 6 - 3 |$ 表示6、3在数轴上对应的两点之间的距离； $| 6 + 3 | = | 6 - (- 3) |$ ，所以 $| 6 + 3 |$ 表示6、 $- 3$ 在数轴上对应的两点之间的距离； $| 6 | = | 6 - 0 |$ ，所以 $| 5 |$ 表示5在数轴上对应的点到原点的距离。

(1)、一般地，点A，B，C在数轴上分别表示有理数x、 $- 2$ 、1，那么A到B的距离与A到C的距离之和可表示为（用含绝对值的式子表示）；

(2)、利用数轴探究：
①满足 $| x - 3 | + | x + 1 | = 6$ 的x的所有值是；
② $| x - 3 | + | x + 1 |$ 的最小值是，此时x的取值范围为.

查看试题解析
13. 请阅读下面的材料，并探索用材料中的方法解决问题．
【材料1】两个含有二次根式而非零的代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式．

例如： $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) = 1$ ，我们称 $\sqrt{3} + \sqrt{2}$ 的一个有理化因式是 $\sqrt{3} - \sqrt{2}$ ．

【材料2】如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含根号，这种变形叫做分母有理化．

例如： $\frac{2}{\sqrt{3} + \sqrt{2}} = \frac{2 (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \frac{2 (\sqrt{3} - \sqrt{2})}{1} = 2 \sqrt{3} - 2 \sqrt{2}$ ．

问题探究：

(1)、写出 $\sqrt{5} - \sqrt{7}$ 的一个有理化因式：_；

(2)、计算： $(2 \sqrt{3} + 3 \sqrt{2}) (2 \sqrt{3} - 3 \sqrt{2}) - {(\sqrt{3} + \sqrt{2})}^{2}$ ；

(3)、将式子 $\frac{22}{2 \sqrt{5} + 3}$ 分母有理化．

查看试题解析
14. 阅读下列材料，回答问题.

(1)、形如 $x^{2} + (p + q) x + p q$ 型的二次三项式，有以下特点：①二次项系数是1；②常数项是两个数之积；③一次项系数是常数项的两个因数之和.
把这个二次三项式进行因式分解，可以这样来解：
$x^{2} + (p + q) x + p q$
$= x^{2} + p x + q x + p q$
$= (x^{2} + p x) + (q x + p q)$
$= x (x + p) q (x + p)$
$= (x + p) (x + q)$ .
因此，可以得 $x^{2} + (p + q) x + p q =$ .
利用上面的结论，可以直接将某些二次项系数为1的二次三项式分解因式；

(2)、利用（1）中的结论，分解因式：
① $m^{2} + 7 m - 18 =$ ；
② $x^{2} - 2 x - 8 =$ ；
③ $x^{2} y^{2} - 7 x y + 10 =$ .

查看试题解析
15. 阅读材料：
已知多项式（a+4）x³+10x²﹣5x+3是关于x的二次多项式，且二次项系数为b，数轴上两点A，B对应的数分别为a，b.

(1)、点A表示的数是，点B表示的数是；

(2)、点A、B同时出发沿数轴向左移动，速度分别为1个单位长度/秒，3个单位长度/秒，经过多少秒，点A与点B相距4个单位？

(3)、点M、N分别从点A、B出发沿数轴向右移动，速度分别为1个单位长度/秒、2个单位长度/秒，点P为ON上靠近点N的三等分点，设OP- $\frac{4}{3}$ AM的值为y，在移动过程中，y值是否发生变化？若不变，求出y值；若变化，说明理由．

查看试题解析
16. 阅读材料：
配方法是初中数学中经常用到的一种重要方法，学好配方法对我们学好数学有很大的帮助，所谓配方就是将某一个多项式变形为一个完全平方式，变形一定要恒等．
例如，解方程x²-4x+4=0，有(x-2)²=0，
∴x=2．
再如，由x²-4x+y²-6y+13=0得：
(x²-4x+4)+(y²-6y+9)=0，
即：(x-2)²+(y-3)²=0，
∴x=2，y=3．
根据上述材料解答下列各题：

(1)、若x²-10x+y²+2y+26=0，求x^y的值．

(2)、若x²-4xy+5y²-2y+1=0，求x+y的值．

(3)、若a，b，c表示三角形ABC的三边长，且a²+b²+c²=ab+bc+ca，试说明：三角形ABC是等边三角形．

查看试题解析
17. 阅读下列材料：我们知道 $| x |$ 表示的是在数轴上数 $x$ 对应的点与原点的距离，即 $| x | = | x - 0 |$ ，也就是说， $| x |$ 表示在数轴上数 $x$ 与数 $0$ 对应点之间的距离 $.$ 这个结论可以推广为 $| x_{1} - x_{2} |$ 表示在数轴上数 $x_{1}$ ， $x_{2}$ 对应点之间的距离．
例如：解方程 $| x | = 6$ ．

解： $∵ | x | = | x - 0 | = 6$ ，

$∴$ 在数轴上与原点距离为 $6$ 的点对应的数为 $\pm 6$ ，即该方程的解为 $x = \pm 6$ ．

【理解应用】根据绝对值的几何意义可以解一些绝对值不等式．

我们定义：形如“ $| x | \leq m$ ， $| x | \geq m$ ， $| x | < m$ ， $| x | > m$ ” $(m$ 为非负数 $)$ 的不等式叫做绝对值不等式，能使一个绝对值不等式成立的所有未知数的值称为绝对值不等式的解集．

由图 $1$ 可以得出：绝对值不等式 $| x | > 1$ 的解集是 $x < - 1$ 或 $x > 1$ ，

绝对值不等式 $| x | \leq 3$ 的解集是 $- 3 \leq x \leq 3$ ．

例如：解不等式 $| x - 1 | > 2$ ．

解：如图 $2$ ，首先在数轴上找出 $| x - 1 | = 2$ 的解，即到 $1$ 的距离为 $2$ 的点对应的数为 $- 1$ ， $3$ ，则 $| x - 1 | > 2$ 的解集为到 $1$ 的距离大于 $2$ 的点对应的所有数，所以原不等式的解集为 $x < - 1$ 或 $x > 3$ ．

参考阅读材料，解答下列问题：

(1)、方程 $| x - 5 | = 3$ 的解为．

(2)、不等式 $| x | \geq 4$ 的解集是．

(3)、不等式 $2 | x + 2 | + 1 < 9$ 的解集是．

(4)、不等式 $| x + 1 | + | x - 3 | > 4$ 的解集是．

(5)、若 $| x - 3 | - | x + 4 | \leq a$ 对任意的 $x$ 都成立，则 $a$ 的取值范围是．

查看试题解析
18. 【阅读材料】把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．配方法在因式分解、最值问题中都有着广泛的应用．例如：
请根据上述材料解决下列问题：

(1)、在横线上添上一个常数项使之成为完全平方式： $a^{2} + 4 a +$ ．

(2)、利用上述方法①进行因式分解： $a^{2} - 10 a + 21$ ．

(3)、参照方法②求 $4 x^{2} + 4 x + 5$ 的最小值．

查看试题解析
19. 先阅读下面的材料，然后回答问题：
方程x+ $\frac{1}{x}$ =2+ $\frac{1}{2}$ 的解为x₁=2，x₂= $\frac{1}{2}$ ；
方程x+ $\frac{1}{x}$ =3+ $\frac{1}{3}$ 的解为x₁=3，x₂= $\frac{1}{3}$ ；
方程x+ $\frac{1}{x}$ =4+ $\frac{1}{4}$ 的解为x₁=4，x₂= $\frac{1}{4}$
……

(1)、观察上述方程的解，猜想关于x的方程x+ $\frac{1}{x}$ =5+ $\frac{1}{5}$ 的解是.

(2)、根据上面的规律，猜想关于x的方程x+ $\frac{1}{x}$ =a+ $\frac{1}{a}$ 的解是.

(3)、猜想关于x的方程x- $\frac{1}{x}$ = $1 \frac{1}{2}$ 的解并验证你的结论

(4)、在解方程y+ $\frac{y + 2}{y + 1}$ = $\frac{10}{3}$ 时，可将方程变形转化为(2)的形式求解，按要求写出你的变形求解过程．

查看试题解析
20. 阅读材料：
在数轴上， $x = 2$ 表示一个点；在平面直角坐标系中， $x = 2$ 表示一条直线；以二元一次方程 $x + y = 2$ 的所有解为坐标的点组成的图形就是一次函数 $y = - x + 2$ 的图象，它也是一条直线.

如图1，在平面直角坐标系中，不等式 $x ⩽ 2$ 表示一个平面区域，即直线 $x = 2$ 及其左侧的部分；

如图2，不等式 $y ⩽ - x + 2$ 也表示一个平面区域，即直线 $y = - x + 2$ 及其下方的部分.

请根据以上材料回答问题：

(1)、图3阴影部分(含边界)表示的是(填写不等式)表示的平面区域；

(2)、如图4，请求出表示阴影部分平面区域(含边界)的不等式组；

(3)、如图5，点 $A$ 在 $x$ 轴上，点 $B$ 的坐标为 $(0 ， 1)$ ，且 $∠ A B O = 6 0^{°}$ ，点 $P$ 为 $△ A B O$ 内部一点(含边界)，过点 $P$ 分别作 $P C ⊥ O A ， P D ⊥ A B ， P E ⊥ B O$ ，垂足分别为C，D，E，若 $P C ⩽ P E ⩽ P D$ ，则所有点 $P$ 组成的平面区域的面积为.

查看试题解析
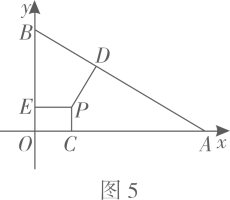21. 阅读理解题：
阅读材料：

如图1，四边形 $A B C D$ 是矩形， $△ A E F$ 是等腰直角三角形，记 $∠ B A E$ 为 $α$ 、 $∠ F A D$ 为 $β$ ，若 $t a n α = \frac{1}{2}$ ，则 $t a n β = \frac{1}{3}$ ．

证明：设 $B E = k$ ， ∵ $t a n α = \frac{1}{2}$ ， ∴ $A B = 2 k$ ，

易证 $△ A E B ≌ △ E F C (A A S)$

∴ $E C = 2 k ， C F = k$ ，

∴ $F D = k ， A D = 3 k$

∴ $t a n β = \frac{D F}{A D} = \frac{k}{3 k} = \frac{1}{3}$ ，

若 $α + β = 45 °$ 时，当 $t a n α = \frac{1}{2}$ ，则 $t a n β = \frac{1}{3}$ ．

同理：若 $α + β = 45 °$ 时，当 $t a n α = \frac{1}{3}$ ，则 $t a n β = \frac{1}{2}$ ．

根据上述材料，完成下列问题：

如图2，直线 $y = 3 x - 9$ 与反比例函数 $y = \frac{m}{x} (x > 0)$ 的图象交于点 $A$ ，与 $x$ 轴交于点 $B$ ．将直线 $A B$ 绕点 $A$ 顺时针旋转 $45 °$ 后的直线与 $y$ 轴交于点 $E$ ，过点 $A$ 作 $A M ⊥ x$ 轴于点 $M$ ，过点 $A$ 作 $A N ⊥ y$ 轴于点 $N$ ，已知 $O A = 5$ ．

(1)、求反比例函数的解析式；

(2)、直接写出 $t a n ∠ B A M 、 t a n ∠ N A E$ 的值；

(3)、求直线 $A E$ 的解析式．

查看试题解析
22. 阅读下列材料：利用完全平方公式，将多项式x²+bx+c变形为（x+m）²+n的形式，然后由（x+m）²≥0就可求出多项式x²+bx+c的最小值．
例题：求多项式x²﹣4x+5的最小值．
解：x²﹣4x+5＝x²﹣4x+4+1＝（x﹣2）²+1，
因为（x﹣2）²≥0，所以（x﹣2）²+1≥1．
当x＝2时，（x﹣2）²+1＝1．因此（x﹣2）²+1有最小值，最小值为1，即x²﹣4x+5的最小值为1．
通过阅读，理解材料的解题思路，请解决以下问题：

(1)、【理解探究】
已知代数式A＝x²+10x+20，则A的最小值为；

(2)、【类比应用】
张大爷家有甲、乙两块长方形菜地，已知甲菜地的两边长分别是（3a+2）米、（2a+5）米，乙菜地的两边长分别是5a米、（a+5）米，试比较这两块菜地的面积S_甲和S_乙的大小，并说明理由；

(3)、【拓展升华】
如图，△ABC中，∠C＝90°，AC＝5cm ， BC＝10cm ，点M、N分别是线段AC和BC上的动点，点M从A点出发以1cm/s的速度向C点运动；同时点N从C点出发以2cm/s的速度向B点运动，当其中一点到达终点时，两点同时停止运动，设运动的时间为t ，则当t的值为多少时，△MCN的面积最大，最大值为多少？

查看试题解析

四、综合题

23. 阅读下面的材料：
如果函数 $y = f (x)$ 满足：对于自变量 $x$ 取值范围内的任意 $x_{1}$ ， $x_{2}$ ，

（ 1 ）若 $x_{1} < x_{2}$ ，都有 $f (x_{1}) < f (x_{2})$ ，则称 $f (x)$ 是增函数；

（ 2 ）若 $x_{1} < x_{2}$ ，都有 $f (x_{1}) > f (x_{2})$ ，则称 $f (x)$ 是减函数.

例题：证明函数 $f (x) = x^{2} (x > 0)$ 是增函数.

证明：任取 $x_{1} < x_{2}$ ，且 $x_{1} > 0$ ， $x_{2} > 0$

则 $f (x_{1}) - f (x_{2}) = x_{1}^{2} - x_{2}^{2} = (x_{1} + x_{2}) (x_{1} - x_{2})$

∵ $x_{1} < x_{2}$ 且 $x_{1} > 0$ ， $x_{2} > 0$

∴ $x_{1} + x_{2} > 0$ ， $x_{1} - x_{2} < 0$

∴ $(x_{1} + x_{2}) (x_{1} - x_{2}) < 0$ ，即 $f (x_{1}) - f (x_{2}) < 0$ ， $f (x_{1}) < f (x_{2})$

∴函数 $f (x) = x^{2} (x > 0)$ 是增函数.

根据以上材料解答下列问题：

(1)、函数 $f (x) = \frac{1}{x} (x > 0)$ ， $f (1) = \frac{1}{1} = 1$ ， $f (2) = \frac{1}{2}$ ， $f (3) =$ ， $f (4) =$ ；

(2)、猜想 $f (x) = \frac{1}{x} (x > 0)$ 是函数 ▲ （填“增”或“减”），并证明你的猜想.

查看试题解析

x	…	－3	－2	－1	1	2	3	…
y	…	2.83	1.73	0	0	1.73	2.83	…

备考2024年中考数学核心素养专题四 数与式的阅读理解

一、选择题

二、填空题

三、实践探究题

四、综合题

备考2024年中考数学核心素养专题四数与式的阅读理解