备考2024年中考数学核心素养专题三 填空题难题突破
试卷更新日期:2024-03-03 类型:二轮复习
一、填空题
-
1. 如 , 我们叫集合M , 其中1,2,x叫做集合M的元素.集合中的元素具有确定性(如x必然存在),互异性(如 , ),无序性(即改变元素的顺序,集合不变).若集合 , 我们说 . 已知集合 , 集合 , 若 , 则的值是 .2. 一只昆虫从点处出发,以每分钟2米的速度在一条直线上运动,它先前进1米,再后退2米,又前进3米,再后退4米,依此规律继续走下去,则运动1小时这只昆虫与点相距米.3. 在 , , , …中,共有个有理数.4. 如图所示,已知△ABC中,∠ACB=90°,∠BAC=30°,BC=1,作AC的垂直平分线交AB于点、交AC于点 , 连接 , 得到第一条线段;作的垂直平分线交AB于点、交于点 , 连接 , 得到第二条线段;作的垂直平分线交AB于点、交于点 , 连接 , 得到第三条线段;……如此作下去,则第n条线段的长为 .
 5. 计算:=6. 如图,在长方形ABCD的边上有P , Q两个动点,速度分别为 , , 两个点同时出发,运动过程中,一个点到达终点停止运D动时,另一个点也停止运动,动点P从C点出发,沿折线向终点A运动,动点Q从A点出发,沿射线向终点B运动,运动时间为t秒.若AB=8m, , 当和的面积之和为12平方米时,t的值为 .
5. 计算:=6. 如图,在长方形ABCD的边上有P , Q两个动点,速度分别为 , , 两个点同时出发,运动过程中,一个点到达终点停止运D动时,另一个点也停止运动,动点P从C点出发,沿折线向终点A运动,动点Q从A点出发,沿射线向终点B运动,运动时间为t秒.若AB=8m, , 当和的面积之和为12平方米时,t的值为 . 7. 若关于 , 的的解是 , 则关于 , 的方程组的解是 .8. 某社区为增强居民体质,体现以人民为中心的理念,准备到一家健身器材专卖店购置一批健身器材供居民健身使用.该专卖店推出两种优惠活动,并规定只能选择其中一种.
7. 若关于 , 的的解是 , 则关于 , 的方程组的解是 .8. 某社区为增强居民体质,体现以人民为中心的理念,准备到一家健身器材专卖店购置一批健身器材供居民健身使用.该专卖店推出两种优惠活动,并规定只能选择其中一种.活动一:所购商品按原价打八折;
活动二:所购商品按原价每满400元减100元.(如:所购商品原价为400元,可减100元,需付款300元;所购商品原价为900元,可减200元,需付款700元)
⑴若购买一件原价为550元的健身器材,更合算的选择方式为活动;
⑵若购买一件原价为元的健身器材,选择活动二比选择活动一更合算,则的取值范围是 .
9. 已知:m2-2m-1=0,n2+2n-1=0且mn≠1,则的值为 .10. 若关于的方程有三个解,则实数的值是 .11. 对于两个不相等的实数a、b , 我们规定符号表示a , b中的较小的值,如 , 按照这个规定,方程的解为 .12. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.设点的运动路程为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高的长为 . 13. 已知直线:与:其中为正整数 , 记 , 与轴围成的三角形面积为 , 则 .14. 如图,在平面直角坐标系 xOy中,点 A(0,4),B(3,4),将△ABO 向右平移到△CDE的位置,点 A 的对应点是点 C,点O的对应点是点 E,函数 的图象经过点 C 和 DE的中点F,则四边形OACE 的面积是.
13. 已知直线:与:其中为正整数 , 记 , 与轴围成的三角形面积为 , 则 .14. 如图,在平面直角坐标系 xOy中,点 A(0,4),B(3,4),将△ABO 向右平移到△CDE的位置,点 A 的对应点是点 C,点O的对应点是点 E,函数 的图象经过点 C 和 DE的中点F,则四边形OACE 的面积是. 15. 如图,在抛物线y=x2的内部依次画正方形,使对角线在y轴上,另两个顶点落在抛物线上.按此规律类推,第2023个正方形的边长是 .
15. 如图,在抛物线y=x2的内部依次画正方形,使对角线在y轴上,另两个顶点落在抛物线上.按此规律类推,第2023个正方形的边长是 . 16. 如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米.
16. 如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米. (1)、如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .(2)、如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .17. 已知点 都在直线 上, , 分别为 中点,直线 上所有线段的长度之和为19,则 .18. 已知 , , 若的一边EF∥BC , 则另一边DE与直线AB相交于点P , 且点E不在直线AB上,则的度数为 .19. 如图, , A、B分别为直线、上两点,且 , 若射线绕点顺时针旋转至后立即回转,射线绕点B逆时针旋转至后立即回转,两射线分别绕点A、点B不停地旋转,若射线转动的速度是/秒,射线转动的速度是/秒,且a、b满足 . 若射线绕点A顺时针先转动18秒,射线才开始绕点B逆时针旋转,在射线到达之前,问射线再转动秒时,射线与射线互相平行.
(1)、如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .(2)、如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .17. 已知点 都在直线 上, , 分别为 中点,直线 上所有线段的长度之和为19,则 .18. 已知 , , 若的一边EF∥BC , 则另一边DE与直线AB相交于点P , 且点E不在直线AB上,则的度数为 .19. 如图, , A、B分别为直线、上两点,且 , 若射线绕点顺时针旋转至后立即回转,射线绕点B逆时针旋转至后立即回转,两射线分别绕点A、点B不停地旋转,若射线转动的速度是/秒,射线转动的速度是/秒,且a、b满足 . 若射线绕点A顺时针先转动18秒,射线才开始绕点B逆时针旋转,在射线到达之前,问射线再转动秒时,射线与射线互相平行. 20. 如图,在等边三角形中, , 点是边上一点,且 , 点是边上一动点(、两点均不与端点重合),作 , 交边于点 . 若 , 当满足条件的点有且只有一个时,则的值为 .
20. 如图,在等边三角形中, , 点是边上一点,且 , 点是边上一动点(、两点均不与端点重合),作 , 交边于点 . 若 , 当满足条件的点有且只有一个时,则的值为 .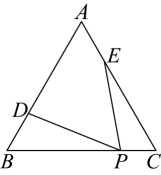 21. 如图,已知 , 点在线段上,是底边长为6的等腰三角形且 , 以为边在的右侧作矩形 , 连接 , 点是的中点,连接 , 则线段的最小值为 .
21. 如图,已知 , 点在线段上,是底边长为6的等腰三角形且 , 以为边在的右侧作矩形 , 连接 , 点是的中点,连接 , 则线段的最小值为 .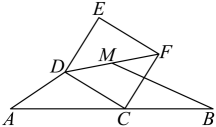 22. 如图,在中, , , 以点为圆心,的长为半径画弧,与边交于点 , 将 绕点旋转后点与点恰好重合,则图中阴影部分的面积为
22. 如图,在中, , , 以点为圆心,的长为半径画弧,与边交于点 , 将 绕点旋转后点与点恰好重合,则图中阴影部分的面积为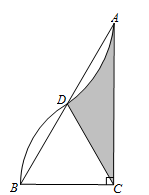 23. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=6,BD=2,以点B为圆心,BD长为半径作圆,点E为上的动点,连结EC,作FC⊥CE,垂足为C,点F在直线BC的上方,且满足 , 连结BF.当点E与点D重合时,BF的值为.点E在上运动过程中,BF存在最大值为.
23. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=6,BD=2,以点B为圆心,BD长为半径作圆,点E为上的动点,连结EC,作FC⊥CE,垂足为C,点F在直线BC的上方,且满足 , 连结BF.当点E与点D重合时,BF的值为.点E在上运动过程中,BF存在最大值为.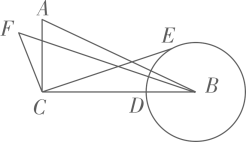 24. 如图,3个大小完全相同的正六边形无缝隙、不重叠的拼在一起,连接正六边形的三个顶点得到 , 则的值是 .
24. 如图,3个大小完全相同的正六边形无缝隙、不重叠的拼在一起,连接正六边形的三个顶点得到 , 则的值是 .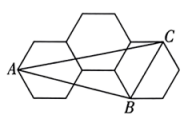 25. 如图1,将一张等腰三角形纸片ABC沿虚线剪开,得到两个全等的三角形和两个全等的四边形小纸片.小博按图2方式拼接,恰好拼成一个不重叠、无缝隙的矩形;小雅按图3方式拼接,也拼出一个矩形FHIK,但由于两个四边形纸片有重叠(阴影)部分,整个面积减少了5cm2.若AE:DE=5∶3,则tanC= , 矩形FHIK的面积为cm2.
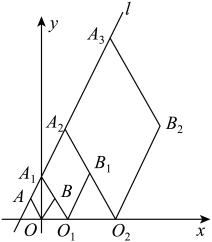
25. 如图1,将一张等腰三角形纸片ABC沿虚线剪开,得到两个全等的三角形和两个全等的四边形小纸片.小博按图2方式拼接,恰好拼成一个不重叠、无缝隙的矩形;小雅按图3方式拼接,也拼出一个矩形FHIK,但由于两个四边形纸片有重叠(阴影)部分,整个面积减少了5cm2.若AE:DE=5∶3,则tanC= , 矩形FHIK的面积为cm2.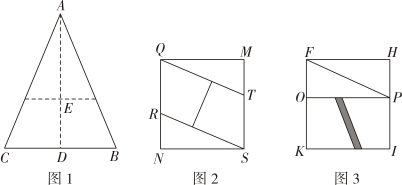 26. 如图,是正三角形,点A在第一象限,点、 . 将线段 绕点C按顺时针方向旋转至;将线段绕点B按顺时针方向旋转至;将线段绕点A按顺时针方向旋转至;将线段绕点C按顺时针方向旋转至;……以此类推,则点的坐标是 .
26. 如图,是正三角形,点A在第一象限,点、 . 将线段 绕点C按顺时针方向旋转至;将线段绕点B按顺时针方向旋转至;将线段绕点A按顺时针方向旋转至;将线段绕点C按顺时针方向旋转至;……以此类推,则点的坐标是 . 27. 如图,在平面直角坐标系中,正方形的顶点A,C的坐标分别为 , .已知线段的端点M,N的坐标分别为 , , 平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,此时正方形被该线段分为两部分,其中三角形部分的面积为;已知线段的端点坐标分别为 , , 且 , , .平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,且线段将正方形的面积分为两部分,取的中点H,连接 , 则的长为.
27. 如图,在平面直角坐标系中,正方形的顶点A,C的坐标分别为 , .已知线段的端点M,N的坐标分别为 , , 平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,此时正方形被该线段分为两部分,其中三角形部分的面积为;已知线段的端点坐标分别为 , , 且 , , .平移线段 , 使得平移后的线段的两个端点均落在正方形的边上,且线段将正方形的面积分为两部分,取的中点H,连接 , 则的长为. 28. 一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,则CD的长为.
28. 一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,则CD的长为.