备考2024年中考数学核心素养专题二 选择题难题突破
试卷更新日期:2024-03-03 类型:二轮复习
一、选择题
-
1. 已知有理数满足 , 则的值是( )A、 B、0或2 C、 D、或2. 对于若干个数,先将每两个数作差,再将这些差的绝对值进行求和,这样的运算称为对这若干个数的“差绝对值运算”,例如,对于 , , 进行“差绝对值运算”,得到: .
对 , , , 进行“差绝对值运算”的结果是;
, , 的“差绝对值运算”的最小值是;
, , 的“差绝对值运算”化简结果可能存在的不同表达式一共有种;
以上说法中正确的个数为( )A、个 B、个 C、个 D、个3. 有一组非负整数: , , …, . 从开始,满足 , , , …, . 某数学小组研究了上述数组,得出以下结论:①当 , 时,;
②当 , 时,;
③当 , , 时,;
④当 , ( , 为整数)时, .
其中正确的结论个数有( )
A、1个 B、2个 C、3个 D、4个4. 已知min{ , x2 , x}表示取三个数中最小的那个数,例如:当x=9,min{ , x2 , x}=min{ , 92 , 9}=3.当min{ , x2 , x}=时,则x的值为( )A、 B、 C、 D、5. 在“点燃我的梦想,数学皆有可能”数学创新设计活动中,“智多星”小强设计了一个数学探究活动,对依次排列的两个整式m,n按如下规律进行操作:第1次操作后得到整式m,n,n-m;
第⒉次操作后得到整式m,n,n-m,-m;
第3次操作后……
其操作规则为:每次操作增加的项,都是用上一次操作得到的最末项减去其前一项的差,小强将这个活动命名为“回头差”游戏.则该“回头差”游戏第2023次操作后得到的整式串各项之和是( )
A、m+n B、m C、n-m D、2n6. 读一读:式子“”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 , 这里“”是求和符号.通过对以上材料的阅读,计算的值为( )A、 B、 C、 D、7. 已知关于的一元一次方程的解为 , 那么关于的一元一次方程的解为( )A、 B、 C、1 D、28. 如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.下列判断正确的是( )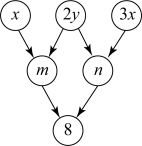
结论 Ⅰ :若n的值为5,则y的值为1;
结论Ⅱ:的值为定值;
结论Ⅲ:若 , 则y的值为4或1.
A、Ⅰ ,Ⅲ均对 B、Ⅱ对,Ⅲ错 C、Ⅱ错,Ⅲ对 D、Ⅰ ,Ⅱ均错9. 定义为不超过x的最大整数,如 , , . 对于任意实数x,下列式子中正确的是( )A、 B、 C、(n为整数) D、10. 若关于的一元一次方程的解为 , 则关于的一元一次方程的解为( )A、 B、 C、 D、11. 已知多项式 , 下列说法正确的个数为( )若 , 则代数式的值为; 当时,代数式的最小值为; 当时,若 , 则的取值范围是 .
A、个 B、个 C、个 D、个12. 已知公式 ( ),则表示 的公式是( )A、 B、 C、 D、13. 如图,四边形是菱形,边长为 , . 点从点出发,沿方向以每秒个单位长度的速度运动,同时点沿射线的方向以每秒1个单位长度的速度运动,当点运动到达点时,点也立刻停止运动,连接 . 的面积为 , 点运动的时间为秒,则能大致反映与之间的函数关系的图像是( )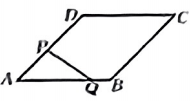 A、
A、 B、
B、 C、
C、 D、
D、 14. 已知和均是以为自变量的函数,为实数.当时,函数值分别为和 , 若存在实数 , 使得.则称和为友好函数,以下和不一定是友好函数的是( )A、和 B、和 C、和 D、和15. 函数图象与有交点 , 且满足 , 则的取值范围是( )A、 B、或2 C、 D、或16. 对于二次函数 , 规定函数是它的相关函数.已知点 , 的坐标分别为 , , 连接 , 若线段与二次函数的相关函数的图象有两个公共点,则的取值范围为( )A、或 B、或 C、或 D、或17. 设函数 , , . 直线x=b的图象与函数y1 , y2 , y3的图象分别交于点A(b , c1),B(b , c2),C(b , c3),( )A、若b<a1<a2<a3 , 则c2<c3<c1 B、若a1<b<a2<a3 , 则c1<c2<c3 C、若a1<a2<b<a3 , 则c3<c2<c1 D、若a1<a2<a3<b , 则c3<c2<c118. 如图,线段 , 动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
14. 已知和均是以为自变量的函数,为实数.当时,函数值分别为和 , 若存在实数 , 使得.则称和为友好函数,以下和不一定是友好函数的是( )A、和 B、和 C、和 D、和15. 函数图象与有交点 , 且满足 , 则的取值范围是( )A、 B、或2 C、 D、或16. 对于二次函数 , 规定函数是它的相关函数.已知点 , 的坐标分别为 , , 连接 , 若线段与二次函数的相关函数的图象有两个公共点,则的取值范围为( )A、或 B、或 C、或 D、或17. 设函数 , , . 直线x=b的图象与函数y1 , y2 , y3的图象分别交于点A(b , c1),B(b , c2),C(b , c3),( )A、若b<a1<a2<a3 , 则c2<c3<c1 B、若a1<b<a2<a3 , 则c1<c2<c3 C、若a1<a2<b<a3 , 则c3<c2<c1 D、若a1<a2<a3<b , 则c3<c2<c118. 如图,线段 , 动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )①运动后,; ②的值随着运动时间的改变而改变;③的值不变;
④当时,运动时间为 .
 A、①② B、②③ C、①②③ D、②③④19. 如图所示,已知直线AB、CD被直线AC所截,是平面内任意一点(点不在直线AB、CD、AC上),设∠BAE , ∠DCE=与均小于 , 在下列各式中:①;②;③;④ , 可能为大小的是( )
A、①② B、②③ C、①②③ D、②③④19. 如图所示,已知直线AB、CD被直线AC所截,是平面内任意一点(点不在直线AB、CD、AC上),设∠BAE , ∠DCE=与均小于 , 在下列各式中:①;②;③;④ , 可能为大小的是( ) A、①②③ B、②③④ C、①②④ D、①②③④20. 如图,在菱形ABCD中,∠A=60°,AB=4.动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A一B一C向终点C运动;点N以每秒1个单位长度沿线段AD向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△AMN的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( )
A、①②③ B、②③④ C、①②④ D、①②③④20. 如图,在菱形ABCD中,∠A=60°,AB=4.动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A一B一C向终点C运动;点N以每秒1个单位长度沿线段AD向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△AMN的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 21. 如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1、∠2的数量关系正确的是( )
21. 如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1、∠2的数量关系正确的是( ) A、∠1+∠2=90° B、2∠1+∠2=180° C、∠1-∠2=90° D、2∠2-∠1=30°22. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A、∠1+∠2=90° B、2∠1+∠2=180° C、∠1-∠2=90° D、2∠2-∠1=30°22. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )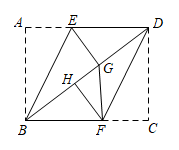 A、BD=10 B、HG=2 C、 D、GF⊥BC23. 如图,四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD , 连结AC , 若正方形ABCD的面积为30,AE+BE=7.则S△CFP﹣S△AEP的值是( )
A、BD=10 B、HG=2 C、 D、GF⊥BC23. 如图,四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD , 连结AC , 若正方形ABCD的面积为30,AE+BE=7.则S△CFP﹣S△AEP的值是( ) A、5.5 B、6.5 C、7 D、7.524. 如图,在扇形中,平分交于点 , 点为半径上一动点.若 , 则阴影部分周长的最小值为( )
A、5.5 B、6.5 C、7 D、7.524. 如图,在扇形中,平分交于点 , 点为半径上一动点.若 , 则阴影部分周长的最小值为( )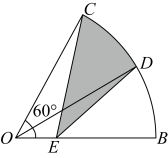 A、 B、 C、 D、25. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )
A、 B、 C、 D、25. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )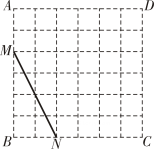 A、 B、6 C、 D、26. 如图,将边长为的正方形绕点逆时针旋转得到正方形 , 与交于点 , 那么图中点的坐标为( )
A、 B、6 C、 D、26. 如图,将边长为的正方形绕点逆时针旋转得到正方形 , 与交于点 , 那么图中点的坐标为( ) A、 B、 C、 D、27. 如图所示,四边形是菱形, , 且 , 作 , 交的延长线于点现将沿的方向平移,得到 , 设 , 与菱形重合的部分图中阴影部分面积为 , 平移距离为 , 则与的函数图象为( )
A、 B、 C、 D、27. 如图所示,四边形是菱形, , 且 , 作 , 交的延长线于点现将沿的方向平移,得到 , 设 , 与菱形重合的部分图中阴影部分面积为 , 平移距离为 , 则与的函数图象为( )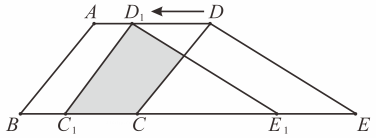 A、
A、 B、
B、 C、
C、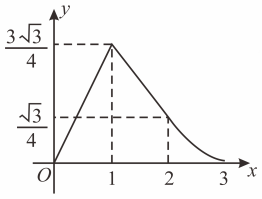 D、
D、 28. 如图①,已知 的斜边 和正方形 的边 都在直线 上( ),且点 与点 重合, 沿直线 向右匀速平移,当点 与点 重合时, 停止运动,设 被 截得的线段长 与 平移的距离 之间的函数图象如图②,则当 时, 和正方形 重合部分的面积为( )
28. 如图①,已知 的斜边 和正方形 的边 都在直线 上( ),且点 与点 重合, 沿直线 向右匀速平移,当点 与点 重合时, 停止运动,设 被 截得的线段长 与 平移的距离 之间的函数图象如图②,则当 时, 和正方形 重合部分的面积为( ) A、 B、 C、 D、29. 如图,在平面直角坐标中,矩形ABCD的边AD=5.OA:OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1位置,点E的坐标是( )
A、 B、 C、 D、29. 如图,在平面直角坐标中,矩形ABCD的边AD=5.OA:OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1位置,点E的坐标是( ) A、(1,2) B、(-1,2) C、(-1,2) D、(1- , 2)30. 在平面直角坐标系中,正方形的位置如图所示,点的坐标为 , 点的坐标为 , 延长交轴于点 , 作正方形;延长交轴于点 , 作正方形;;按这样的规律进行下去,正方形的面积为( )
A、(1,2) B、(-1,2) C、(-1,2) D、(1- , 2)30. 在平面直角坐标系中,正方形的位置如图所示,点的坐标为 , 点的坐标为 , 延长交轴于点 , 作正方形;延长交轴于点 , 作正方形;;按这样的规律进行下去,正方形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、

