【培优卷】北师大版数学八(下)第三章图形的平移与旋转 章末检测
试卷更新日期:2024-03-03 类型:单元试卷
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 下列关于数字变换的图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图案中,不能由一个图形通过旋转而形成的是( )A、
2. 下列图案中,不能由一个图形通过旋转而形成的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列图形中,能由图形通过平移得到的是( )
3. 下列图形中,能由图形通过平移得到的是( )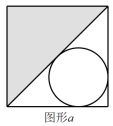 A、
A、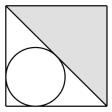 B、
B、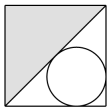 C、
C、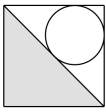 D、
D、 4. 下列各组图形中,△ A'B'C'与 △ABC 成中心对称的是( )A、
4. 下列各组图形中,△ A'B'C'与 △ABC 成中心对称的是( )A、 B、
B、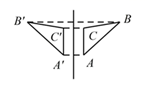 C、
C、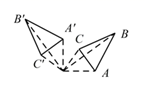 D、
D、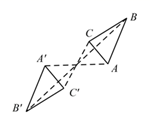 5. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.
5. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.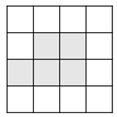 A、2 B、3 C、4 D、56. 如图,将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形,至少需要移动 ( )
A、2 B、3 C、4 D、56. 如图,将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形,至少需要移动 ( ) A、12格 B、11格 C、9 格 D、8格7. 下列图形中,周长最长的是( )A、
A、12格 B、11格 C、9 格 D、8格7. 下列图形中,周长最长的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,∠AOB=90°,∠B=30°,将△AOB绕点O顺时针旋转角度得到△A′OB′,旋转角为α.若点A′落在AB上,则旋转角α的大小是( )
8. 如图,∠AOB=90°,∠B=30°,将△AOB绕点O顺时针旋转角度得到△A′OB′,旋转角为α.若点A′落在AB上,则旋转角α的大小是( ) A、30° B、45° C、60° D、90°9. 如图,在直角三角形ABC中,∠BAC=90°,把三角形ABC沿射线 BC 的方向平移2.5cm 后得到三角形DEF,连结AE,AD.有以下结论:①AC∥DF;②AD∥BE;③CF=2.5cm;④DE⊥AC.其中正确的个数是( )
A、30° B、45° C、60° D、90°9. 如图,在直角三角形ABC中,∠BAC=90°,把三角形ABC沿射线 BC 的方向平移2.5cm 后得到三角形DEF,连结AE,AD.有以下结论:①AC∥DF;②AD∥BE;③CF=2.5cm;④DE⊥AC.其中正确的个数是( ) A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,已知点 , 点.以点为旋转中心,把点按逆时针方向旋转 , 得到点.在 , 四个点中,直线PB经过的点是( )
A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,已知点 , 点.以点为旋转中心,把点按逆时针方向旋转 , 得到点.在 , 四个点中,直线PB经过的点是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,每小题3分,共15分)
-
11. 如图,△AOB与△OOD关于点O成中心对称,已知∠BAO=90°,AB=4,AO=3,则AD的长为
 12. 如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .
12. 如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .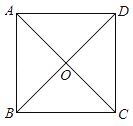 13. 如图,在平面直角坐标系中,的顶点 , 的坐标分别为 , , 把沿轴向右平移得到 , 如果点的坐标为 , 则点的坐标为 .
13. 如图,在平面直角坐标系中,的顶点 , 的坐标分别为 , , 把沿轴向右平移得到 , 如果点的坐标为 , 则点的坐标为 . 14. 如图,在平面直角坐标系中,一动点从原点O出发,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0)…,则点P2023的坐标是 .
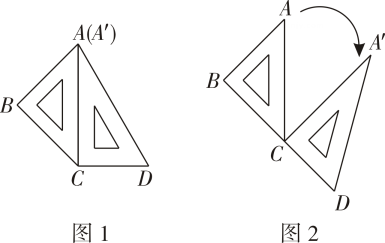
14. 如图,在平面直角坐标系中,一动点从原点O出发,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0)…,则点P2023的坐标是 .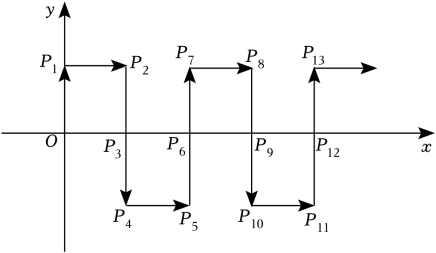 15. 两块不同的三角板按如图1所示摆放,边与边重合, , 接着如图2保持三角板不动,将三角板绕着点(点不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于时,停止旋转,在此旋转过程中,时,三角板有一条边与三角板的一条边恰好平行.
15. 两块不同的三角板按如图1所示摆放,边与边重合, , 接着如图2保持三角板不动,将三角板绕着点(点不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于时,停止旋转,在此旋转过程中,时,三角板有一条边与三角板的一条边恰好平行.
三、作图题(共3题,共20分)
-
16. 如图是由小正方形组成的网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.三角形中任意一点经过平移变换后对应点 , 将三角形作同样的平移变换得到三角形 . (点、、的对应点分别是点、、)
 (1)、画出平移后的三角形;(2)、连接 , , 则;(3)、为轴上一动点,当最小时,画出点并直接写点的坐标 ▲ .17. 如图是由边长为 的小正方形构成的网格.每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)、画出平移后的三角形;(2)、连接 , , 则;(3)、为轴上一动点,当最小时,画出点并直接写点的坐标 ▲ .17. 如图是由边长为 的小正方形构成的网格.每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题: (1)、将边 绕点 逆时针旋转 得到线段 ;(2)、画 的高 ;(3)、将点 竖直向下平移 个单位长度得到点 ,画出点 ;(4)、画线段 关于直线 的对称线段 .18. 已知三个顶点的坐标分别为 , , .
(1)、将边 绕点 逆时针旋转 得到线段 ;(2)、画 的高 ;(3)、将点 竖直向下平移 个单位长度得到点 ,画出点 ;(4)、画线段 关于直线 的对称线段 .18. 已知三个顶点的坐标分别为 , , . (1)、作关于点成中心对称的(点的对应点为 , 点的对应点为);(2)、把向右平移3个单位,作出平移后的(点的对应点为 , 点的对应点为 , 点的对应点为);(3)、轴上存在点 , 使得的值最小,则点的坐标是
(1)、作关于点成中心对称的(点的对应点为 , 点的对应点为);(2)、把向右平移3个单位,作出平移后的(点的对应点为 , 点的对应点为 , 点的对应点为);(3)、轴上存在点 , 使得的值最小,则点的坐标是四、解答题(共9分)
-
19. 在中, , , 直线经过点 , 且于 , 于 ,
 (1)、当直线绕点旋转到图的位置时,求证:;(2)、当直线绕点旋转到图的位置时,求证:;(3)、当直线绕点旋转到图的位置时,试问、、具有怎样的等量关系?请直接写出这个等量关系.
(1)、当直线绕点旋转到图的位置时,求证:;(2)、当直线绕点旋转到图的位置时,求证:;(3)、当直线绕点旋转到图的位置时,试问、、具有怎样的等量关系?请直接写出这个等量关系.五、实践探究题(共3题共26分)
-
20. 在平面直角坐标系中,点 , 过点P作轴,垂足为点H,给出如下定义:将点H向右平移个单位,得到点Q,则称点Q是点P关于x轴的折对点;当时,则称d为点P关于点Q的折对距离.
 (1)、点关于x轴的折对点的坐标是 , 折对距离为;(2)、点Q是点P关于x轴的折对点,若折对点 , 写出一个符合条件的P点坐标;(3)、已知点 , , 以线段AB为边,在x轴上方作正方形 , 在正方形上存在点P,且点P关于点Q的折对距离 , 直接写出t的取值范围.21. 知识背景:
(1)、点关于x轴的折对点的坐标是 , 折对距离为;(2)、点Q是点P关于x轴的折对点,若折对点 , 写出一个符合条件的P点坐标;(3)、已知点 , , 以线段AB为边,在x轴上方作正方形 , 在正方形上存在点P,且点P关于点Q的折对距离 , 直接写出t的取值范围.21. 知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
 (1)、如图1,直线m 经过▱ABCD对角线的交点 O,则(填“〉”“〈”或“=”).(2)、将两个正方形按如图2 所示的方式摆放,O为小正方形对角线的交点,作过点 O 且将整个图形分成面积相等的两部分的直线.(3)、将8个大小相同的正方形按如图3 所示的方式摆放,作将整个图形分成面积相等的两部分的直线(用三种不同的方法).22. 问题情境:在学习图形的平移和旋转时,数学兴趣小组遇到这样一个问题:如图 , 点为等边的边上一点,将线段绕点逆时针旋转得到线段 , 连接 .
(1)、如图1,直线m 经过▱ABCD对角线的交点 O,则(填“〉”“〈”或“=”).(2)、将两个正方形按如图2 所示的方式摆放,O为小正方形对角线的交点,作过点 O 且将整个图形分成面积相等的两部分的直线.(3)、将8个大小相同的正方形按如图3 所示的方式摆放,作将整个图形分成面积相等的两部分的直线(用三种不同的方法).22. 问题情境:在学习图形的平移和旋转时,数学兴趣小组遇到这样一个问题:如图 , 点为等边的边上一点,将线段绕点逆时针旋转得到线段 , 连接 .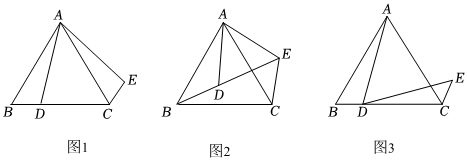 (1)、【猜想证明】试猜想与的数量关系,并加以证明;(2)、【探究应用】如图 , 点为等边内一点,将线段绕点逆时针旋转得到线段 , 连接 , 若、、三点共线,求证:平分;(3)、【拓展提升】如图 , 若是边长为的等边三角形,点是线段上的动点,将线段绕点顺时针旋转得到线段 , 连接点在运动过程中,的周长最小值直接写答案 .
(1)、【猜想证明】试猜想与的数量关系,并加以证明;(2)、【探究应用】如图 , 点为等边内一点,将线段绕点逆时针旋转得到线段 , 连接 , 若、、三点共线,求证:平分;(3)、【拓展提升】如图 , 若是边长为的等边三角形,点是线段上的动点,将线段绕点顺时针旋转得到线段 , 连接点在运动过程中,的周长最小值直接写答案 .
-