【培优卷】2024年北师大版数学八(下)3.1图形的平移 同步练习
试卷更新日期:2024-03-03 类型:同步测试
一、选择题
-
1. 如图, , 则AB的长为( )
 A、 B、10 C、 D、2. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动;第一次将点A向左移动3个单位长度到达点 ,第二次将点A向右移动6个单位长度到达点 ,第三次将点 向左移动9个单位长度到达点 ,按照这种移动规律移动下去,第n次移动到点 ,如果点 与原点的距离不小于17,那么n的最小值是( )
A、 B、10 C、 D、2. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动;第一次将点A向左移动3个单位长度到达点 ,第二次将点A向右移动6个单位长度到达点 ,第三次将点 向左移动9个单位长度到达点 ,按照这种移动规律移动下去,第n次移动到点 ,如果点 与原点的距离不小于17,那么n的最小值是( )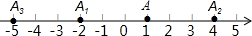 A、9 B、10 C、11 D、123. 把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中,已知这两个大长方形的长比宽长 , 若记图2中阴影部分的周长为 , 图3中阴影部分的周长为 , 那么( )
A、9 B、10 C、11 D、123. 把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中,已知这两个大长方形的长比宽长 , 若记图2中阴影部分的周长为 , 图3中阴影部分的周长为 , 那么( )
图1 图2 图3
A、 B、 C、 D、4. 已知矩形ABCD,将两张边长分别为和的正方形纸片按图1,图2两种方式放置(图1,图2两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1与图2中阴影部分的周长差为 , 若要知道的值,只需测量( )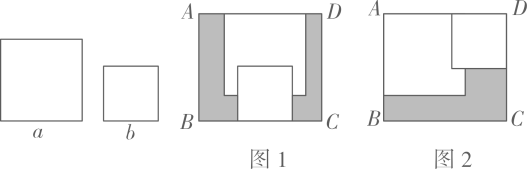 A、 B、 C、BC D、AB5. 如图,点 ,点 向上平移1个单位,再向右平移2个单位.得到 ;点 向上平移2个单位,再向右平移4个单位,得到点 ;点 向上平移4个单位,再向右平移8个单位,得到点 ……按照这个规律得到 ,则点 的横坐标为( )
A、 B、 C、BC D、AB5. 如图,点 ,点 向上平移1个单位,再向右平移2个单位.得到 ;点 向上平移2个单位,再向右平移4个单位,得到点 ;点 向上平移4个单位,再向右平移8个单位,得到点 ……按照这个规律得到 ,则点 的横坐标为( )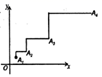 A、 B、 C、 D、6. 如图,在三角形ABC中, , , , , 将三角形沿射线的方向平移个单位长度得到三角形 , 连接 , 则下列结论:①且;②四边形的面积等于四边形DFCG的面积;③四边形的周长为;④其中正确结论的个数为( )
A、 B、 C、 D、6. 如图,在三角形ABC中, , , , , 将三角形沿射线的方向平移个单位长度得到三角形 , 连接 , 则下列结论:①且;②四边形的面积等于四边形DFCG的面积;③四边形的周长为;④其中正确结论的个数为( )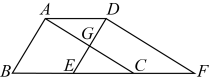 A、1个 B、2个 C、3个 D、4个7. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )
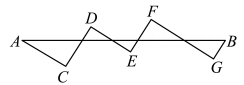
A、1个 B、2个 C、3个 D、4个7. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )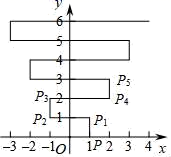 A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)8. 以某公园西门O为原点建立平面直角坐标系,东门A和景点B的坐标分别是和 . 如图1,甲的游览路线是: , 其折线段的路程总长记为 . 如图2,景点C和D分别在线段上,乙的游览路线是: , 其折线段的路程总长记为 . 如图3,景点E和G分别在线段上,景点F在线段上,丙的游览路线是: , 其折线段的路程总长记为 . 下列 , , 的大小关系正确的是( )
A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)8. 以某公园西门O为原点建立平面直角坐标系,东门A和景点B的坐标分别是和 . 如图1,甲的游览路线是: , 其折线段的路程总长记为 . 如图2,景点C和D分别在线段上,乙的游览路线是: , 其折线段的路程总长记为 . 如图3,景点E和G分别在线段上,景点F在线段上,丙的游览路线是: , 其折线段的路程总长记为 . 下列 , , 的大小关系正确的是( )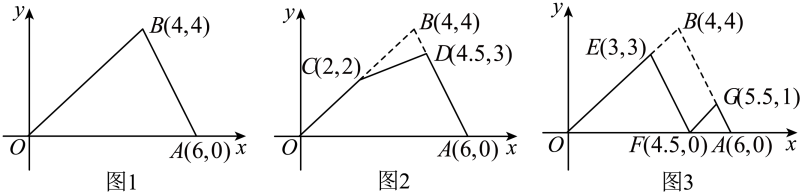 A、 B、且 C、 D、且
A、 B、且 C、 D、且二、填空题
-
9. 已知中, , , 若沿射线方向平移m个单位得到 , 顶点A , B , C分别与顶点D , E , F对应,若以点A , D , E为顶点的三角形是等腰三角形,则m的值是 .10. 如图,把一块三角板放在直角坐标系第一象限内,其中30°角的顶点A落在y轴上,直角顶点C落在x轴的( ,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为 .
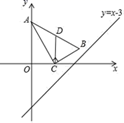 11. 如图,在平面直角坐标系中,对正方形及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度 , 得到正方形及其内部的点,其中点A,B的对应点分别为 , . 已知正方形内部的一点F经过上述操作后得到的对应点与点F重合.
11. 如图,在平面直角坐标系中,对正方形及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度 , 得到正方形及其内部的点,其中点A,B的对应点分别为 , . 已知正方形内部的一点F经过上述操作后得到的对应点与点F重合. (1)、 , .(2)、点F的坐标是 .12. 如图,在直角坐标系中,一只蚂蚁从原点O出发,按向上、向右、向下、向右的方式依次移动,每次移动1个单位.其行走路线如图所示.
(1)、 , .(2)、点F的坐标是 .12. 如图,在直角坐标系中,一只蚂蚁从原点O出发,按向上、向右、向下、向右的方式依次移动,每次移动1个单位.其行走路线如图所示. (1)、填写下列各点的坐标:
(1)、填写下列各点的坐标:A1( ),A3( ),A12()
(2)、写出点A4n的坐标(n是正整数):An().(3)、蚂蚁从点A2019到A2020的移动方向是三、作图题
-
13. 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点)和直线l.
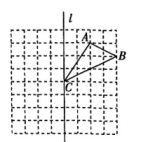 (1)、在直线l上找一点P,使点P到边AB,BC的距离相等;(2)、画出△ABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;(3)、结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是
(1)、在直线l上找一点P,使点P到边AB,BC的距离相等;(2)、画出△ABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;(3)、结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是(A)对应点连线互相平行.
(B)对应点连线被直线l垂直平分.
(C)对应点连线被直线l平分或与直线l重合.
14. 在平面直角坐标系中,的三个顶点分别是 , , .(1)、在所给的图中,画出这个平面直角坐标系;(2)、点经过平移后对应点为 , 将作同样的平移得到 , 画出平移后的;(3)、在(2)的条件下,点在直线上,若 , 直接写出点的坐标;(4)、在(2)的条件下,已知 , 点 , 点 , 所围成的区域内包括边界恰有个整点,求的取值范围.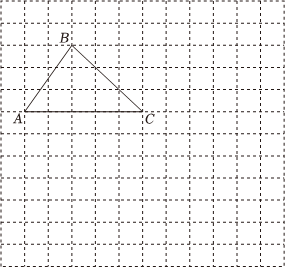
四、解答题
-
15. 在平面直角坐标系中,对于点 , 若点Q的坐标为 , 则称点Q是点P的“a阶派生点”(其中a为常数,且).例如:点的“2阶派生点”为点 , 即点 .(1)、若点P的坐标为 , 则它的“3阶派生点”的坐标为;(2)、若点P的“5阶派生点”的坐标为 , 求点P的坐标;(3)、若点P先向左平移2个单位长度,再向上平移1个单位长度后得到了点 , 点的“阶派生点”位于坐标轴上,求点P2的坐标.16. 如图,在平面直角坐标系中,点A,B的坐标分别为(3,5),(3,0).将线段AB向下平移2个单位长度,再向左平移4个单位长度,得到线段CD,连接AC,BD.
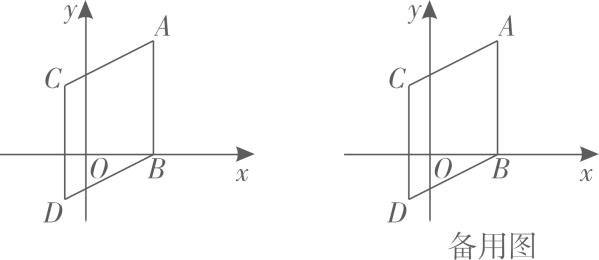 (1)、直接写出坐标:点C( , ),点D( , );(2)、M,N分别是线段AB,CD上的动点,点M从点A出发向点B运动,速度为每秒1个单位长度,点N从点D出发向点C运动,速度为每秒0.5个单位长度,若两点同时出发,求几秒后MN∥x轴?(3)、若点P是x轴正半轴上一动点(不与点B重合),问∠DCP、∠CPA与∠PAB存在怎样的数量关系?请直接写出结论.
(1)、直接写出坐标:点C( , ),点D( , );(2)、M,N分别是线段AB,CD上的动点,点M从点A出发向点B运动,速度为每秒1个单位长度,点N从点D出发向点C运动,速度为每秒0.5个单位长度,若两点同时出发,求几秒后MN∥x轴?(3)、若点P是x轴正半轴上一动点(不与点B重合),问∠DCP、∠CPA与∠PAB存在怎样的数量关系?请直接写出结论.