备考2024年浙江中考数学一轮复习专题31.1统计与概率基础夯实

试卷更新日期：2024-03-03 类型：一轮复习

进入出卷网下载

一、选择题（每题2分，共20分）

1. 动物园中有熊猫、孔雀、大象、梅花鹿四种可爱的动物，为了了解本班同学喜欢哪种动物的人最多，调查的对象应是（）．

A、本班的每一个同学 B、熊猫、孔雀、大象、梅花鹿 C、同学们的选票 D、记录下来的数据

查看试题解析
2. 为了调查不同面额纸币上细菌数量与使用频率之间的关系，某中学研究性学习小组从银行、商店、农贸市场及医院收费处随机采集了6种面额纸币各30张，分别用无菌生理盐水溶液清洗这些纸币，对洗出液进行细菌培养，测得细菌如下表：
面额
5角
1元
5元
10元
20元
100元
细菌总数(个/30张)
147400
381150
98800
145500
27500
12250
获得这组数据方法是（）

A、直接观察 B、调查 C、互联网查询 D、实验

查看试题解析
3. 小红同学对数据24，48，23，24，5■，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
4. 某班共有 $48$ 名学生，体育课上老师统计全班一分钟仰卧起坐的个数，由于小亮没有参加此次集体测试，因此计算其他 $47$ 名学生一分钟仰卧起坐的平均个数为 $30$ 个，方差为 $15 .$ 后来小亮进行了补测，成绩为 $30$ 个，关于该班 $48$ 名学生的一分钟仰卧起坐个数，下列说法正确的是（）

A、平均个数不变，方差不变 B、平均个数变小，方差不变 C、平均个数变大，方差变大 D、平均个数不变，方差变小

查看试题解析
5. 小楠所在社会实践活动小组的同学们响应“垃圾分类，从我做起”的号召，主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示，那么这组数据的众数和中位数分别是（）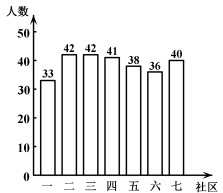

A、42，40 B、42，38 C、2，40 D、2，38

查看试题解析
6. 下列说法正确的是（）

A、为了解全国中学生的课外阅读情况，应采取全面调查的方式 B、为了解九年级1200名学生模拟考试的数学成绩，从中抽取200名学生的数学成绩进行调查，这个问题中样本容量为1200 C、投掷一枚硬币100次，一定有50次“正面朝上” D、甲、乙两名学生参加“国学小名士”知识竞赛选拔赛成绩的平均数均为94，方差分别为5.3和4.8，则乙学生的成绩稳定

查看试题解析
7. 一个口袋中有红球、黄球共20个，这些除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一球，记下颜色后再放回口袋，不断重复这一过程，共摸了200次，发现其中有161次摸到红球．则这个口袋中红球数大约有（　　）

A、4个 B、10个 C、16个 D、20个

查看试题解析
8. 下列事件是必然事件的为（）

A、明天早上会下雨 B、任意一个三角形，它的内角和等于180° C、掷一枚硬币，正面朝上 D、打开电视机，正在播放“瑞安新闻”

查看试题解析
9. 某射击运动员在同一条件下的射击成绩记录如下：
射击次数
20
80
100
200
400
1000
“射中8环以上”的次数
18
68
82
168
327
823
“射中8环以上”的频率（结果保留两位小数）
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性，估计这名运动员射击一次时“射中8环以上”的概率约是（）

A、0.90 B、0.82 C、0.85 D、0.84

查看试题解析
10. 以下说法合理的是（）

A、小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是 $\frac{2}{3}$ B、某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖 C、小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是 $\frac{1}{2}$ D、某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是 $\frac{1}{2}$

查看试题解析

二、填空题（每题3分，共18分）

11. 要了解某中学七年级（1）班学生的视力情况，比较合适的调查方法是．（填“全面调查”或“抽样调查”中的一个）．

查看试题解析
12. 经调查：某地青少年、成年人、老年人的人口比为2：4：4．现要抽取一个样本容量为1000的样本，青少年人数为人，成年人人数为人．

查看试题解析
13. 若一组数据 1，2，3，x的平均数是2，则这组数据的方差是．

查看试题解析
14. 如果一组数据由四个整数组成，其中三个分别是2，4，6，且这组数据的中位数也是整数，那么这组数据的中位数是．

查看试题解析
15. 一个盒子中有m个红球、3个白球，每个球除颜色外都相同．从中任取一个球，若取得白球的概率是 $\frac{1}{4}$ 则m= ．

查看试题解析
16. 如图，在 $3 \times 3$ 的正方形网格中，有三块小正方形被涂黑色，其余均为白色，现任选一个白色的小正方形涂黑，使黑色部分所构成的图形是中心对称图形的概率是．

查看试题解析

三、解答题（共10题，共82分）

17. 在一个不透明的口袋中装有若干个相同的红球，为估计袋中红球的数量，九（1）班学生分组进行摸球试验：每组先将10个与红球形状大小完全相同的白球装入袋中，搅匀后随机摸出一个球并记下颜色，再把它放回袋中，不断重复.以下是这次活动统计汇总各小组数据后获得的全班数据统计表：
摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率 $\frac{n}{s}$
0.420
0.410
0.412
0.406
0.403
b

(1)、按表格数据格式，表中的a=；b=；

(2)、请估计：当次数s很大时，摸到白球的频率将会接近（精确到0.1）；

(3)、请推算：摸到红球的概率是（精确到0.1）；

(4)、试估算：这一个不透明的口袋中红球有个.

查看试题解析
18.
某商场设定了一个可以自由转动的转盘（转盘被等分成16个扇形），并规定：顾客在商场消费每满200元，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红、黄和蓝色区域，顾客就可以分别获得50元、30元和10元的购物券．如果顾客不愿意转转盘，则可以直接获得购物券15元．

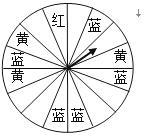(1)、转动一次转盘，获得50元、30元、10元购物券的概率分别是多少？

(2)、如果有一名顾客在商场消费了200元，通过计算说明转转盘和直接获得购物券，哪种方式对这位顾客更合算？

查看试题解析
19. 如图是两个转盘，每个转盘都被圆的半径三等分，甲转盘的三个扇形上标有数字2，4，6，乙转盘的三个扇形上标有数字1，3，5，小明和小力分别转动甲、乙转盘，每入转动一次，记录转盘停止后指针指向的数字，若指针指在分界线上则重转．

(1)、两人分别转动甲、乙转盘后，可能出现的全部可能有哪些？请用列表或画树状图的方法表示．

(2)、若得到的两数字之和是3的倍数，则小明赢；若得到的两数字之和是7的倍数，则小力赢，此游戏公平吗？为什么？

查看试题解析
20. 有一道满分12分的解答题，按评分标准，所有考生的得分只有四种：0分，4分，8分，12分．老师为了了解学生的得分情况与题目的难易情况，从所有考生的试卷中随机抽取一部分，通过分析与整理，绘制了如下两幅图不完整的统计图．
请根据以上信息解答下列问题：

(1)、填空： a= ，b= ．并把条形统计图补全；

(2)、已知难度系数的计算公式为L= $\frac{X}{W}$ ，其中I为难度系数，X为样本平均得分，W为试题满分值．一般来说，根据试题的难度系数可将试题分为以下三类：当0≤L≤0.4时，此题为难题；当0.4<L≤0.7时，此题为中等难度试题；当0.7<L≤1时，此题为容易题．试问此题对于这些考生来说属于哪一类？请说明理由．

查看试题解析
21. 某教育部门为了解本地区中小学生参加家庭劳动时间的情况，随机抽取该地区1200名中小学生进行问卷调查，并将调查问卷（部分）和结果描述如下：
中小学生每周参加家庭劳动时间x（h）分为5组：第一组（0≤x<0.5），第二组（0.5≤x<1），第三组（1≤x<1.5），第四组（1.5≤x<2），第五组（x≥2）．根据以上信息，解答下列问题：

(1)、本次调查中，中小学生每周参加家庭劳动时间的中位数落在哪一组？

(2)、在本次被调查的中小学生中，选择“不喜欢”的人数为多少？

(3)、该教育部门倡议本地区中小学生每周参加家庭劳动时间不少于2h，请结合上述统计图，对该地区中小学生每周参加家庭劳动时间的情况作出评价，并提出两条合理化建议．
.

查看试题解析

22. 根据以下素材，探索完成“问题解决”中的任务1和任务2.

让学生了解班级粮食浪费现状，体会浪费粮食的危害

背景

为了解落实“光盘行动”的情况，某校同学调研了七、八年级部分班级某一天的餐厨垃圾质量．

素材1

从七、八年级中随机抽取了10个班的餐厨垃圾质量，数据如下（单位： $k g$ ）

七年级	$0.8$	$0.9$	$0.8$	$0.8$	$1.1$	$1.7$	$2.3$	$1.1$	$1.9$	$1.6$
八年级	$1.0$	$\begin{array}{l} 0.9 \end{array}$	$\begin{array}{l} 1.3 \end{array}$	$1.0$	$1.9$	$1.0$	$\begin{array}{l} 0.9 \end{array}$	$\begin{array}{l} 1.7 \end{array}$	$\begin{array}{l} 2.3 \end{array}$	$1.0$

素材2

餐厨垃圾质量用x表示，分四个等级：

A： $x < 1$ ；

B： $1 \leq x < 1.5$ ；

C： $1.5 < x < 2$ ；

D： $x \geq 2$ ．

（备注：餐厨垃圾质量越小，说明光盘行动落实越到位）

素材3

七八年级抽取的班级餐厨垃圾数据分析表

年级	平均数	中位数	众数	方差	A等级所占百分比
七年级	a	$1.1$	$0.8$	$\begin{array}{l} 0.26 \end{array}$	$40 %$
八年级	$1.3$	b	$1.0$	$\begin{array}{l} 0.22 \end{array}$	c

问题解决

任务1

数据处理

（1）求出素材3表格中的a，b，c的值；

任务2

数据分析

（2）根据以上数据，你认为该校七、八年级的“光盘行动”，哪个年级落实得更好，请说明理由（写出一条理由即可）．

查看试题解析

23. 某市在九年级“线上教学”结束后，为了解学生的视力情况，抽查了部分学生进行视力检测。根据检测结果，制成下面不完整的统计图表。

被抽样的学生视力情况频数表

组别	视力段	频数
A	5.1≤x≤5.3	25
B	4.8≤x≤5.0	115
C	4.4≤x≤4.7	m
D	4.0≤x≤4.3	52

(1)、求组别C的频数m的值。

(2)、求组别A的圆心角度数。

(3)、如果视力值4.8及以上属于“视力良好”，请估计该市25000名九年级学生达到“视力良好”的人数。根据上述图表信息，你对视力保护有什么建议？

查看试题解析

24. 为了解全校1200名学生假期一周内平均每天在家体育锻炼时间的情况，随机调查了该校100名学生一周内平均每天在家体育锻炼时间的情况，结果如下表，根据信息完成下列问题：

时间（分）	20	30	40	50	60
人数	34	27	20	13	6

(1)、根据统计表信息，直接写出这100名学生一周内平均每天在家体育锻炼时间的平均数、中位数和众数．

(2)、请估计该校一周内平均每天在家体育锻炼时间不少于40分钟的学生大约有多少人？

(3)、学校要给学生制定每天的锻炼目标，为了提高学生的锻炼积极性并且使一半以上的学生能达标，如果你是决策者，从平均数、中位数、众数的角度进行分析，你将选择哪个统计量作为“达标标准”，简要说明理由．

查看试题解析

25. 千岛湖某学校想知道学生对“大下姜”，“沪马公园”，“月光之恋”等旅游景点的了解程度，随机抽查了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必须且只能选一项）：A．不知道，B．了解较少，C．了解较多，D．十分了解．将问卷调查的结果绘制成如下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：

(1)、本次调查了多少名学生？

(2)、根据调查信息补全条形统计图；

(3)、该校共有1800名学生，请你估计“十分了解”的学生共有多少名？

(4)、在被调查“十分了解”的学生中，有四名同学普通话较好，他们中有2名男生和2名女生，学校想从这四名同学中任选两名同学，做家乡旅游品牌的宣传员，请你用列表法或画树状图法，求出被选中的两人恰好是一男一女的概率．

查看试题解析

26. 称五筐大白菜的重量，得到如下统计表中甲组数据．把甲组数据的每个数都减去

40

，得到统计表中的乙组数据，将这两组数据分别画成折线统计图（未完成．单位：千克）．

甲组、乙组数据统计表

序号	1	2	3	4	5
甲组数据	$38$	$42$	$38$	$39$	$43$
乙组数据	$- 2$	2	$- 2$	$- 1$	3

请完成下列问题：

(1)、完成乙组数据的折线统计图．

(2)、①分别求出甲、乙两组数据的平均数

\bar{x_{甲}}

，

\bar{x_{乙}}

，并直接写出

\bar{x_{甲}}

与

\bar{x_{乙}}

之间满足的数量关系式．

②甲、乙两组数据的方差分别为 ${S^{2}}_{甲}$ ， ${S^{2}}_{乙}$ ，请比较 ${S^{2}}_{甲}$ ， ${S^{2}}_{乙}$ 的大小，并说明理由．

查看试题解析