备考2024年浙江中考数学一轮复习专题30.1图形与坐标 基础夯实

试卷更新日期：2024-03-03 类型：一轮复习

进入 出卷网 下载

一、选择题（每题2分，共20分）

  • 1. 台风是一种破坏性极大的自然灾害，气象台为了预报台风，首先应确定台风中心的位置．下列表述能确定台风中心位置的是（   ）
    A、在沿海地区 B、台湾省以东的洋面上 C、距离台州200km D、北纬28°，东经120°

    查看试题解析

  • 2. 小嘉去电影院观看《长津湖》，如果用(5，7)表示5排7座，那么小嘉坐在7排8座可表示为（    )
    A、(5，7) B、(7，8） C、(8，7) D、(T，5)

    查看试题解析

  • 3. 下列叙述中，不能确定位置的是（ ）
    A、小华在某会场的座位是5排8号 B、某城市位于东经108°，北纬39° C、A城与B城相距15 km D、船C在观测点A北偏东40°方向上30 km处

    查看试题解析

  • 4. 如图是画在方格纸上的温州部分旅游景点简图．建立直角坐标系后，狮子岩、永嘉书院与埭头古村的坐标分别是(3，2)，(-1，-3)，(-3，0)，下列地点中离原点最近的是（ ）

    A、狮子岩 B、龙瀑仙洞 C、埭头古村 D、永嘉书院

    查看试题解析

  • 5. 点P坐标为（2-a ， 3a+6） ， 且点P到两坐标轴的距离相等，则点P的坐标是（    ）
    A、（3 ， 3） B、（3 ， -3） C、（3 ， -3）或（6 ， -6） D、（3 ， 3）或（6 ， -6）

    查看试题解析

  • 6. 如图，四盏相同的灯笼放置在平面直角坐标系中，坐标分别是A(-3.5，b)，B(-2，b)，C(-1，b)，D(1，b)，将其中一盏灯笼向右平移m个单位，使得y轴两侧的灯笼对称，则m的值可以是（ ）

    A、3 B、4 C、4.5 D、5.5

    查看试题解析

  • 7. 在平面直角坐标系中，将点A(m−1 ， n+2)先向右平移3个单位，再向上平移2个单位，得到点A'.若点A'位于第四象限，则m、n的取值范围分别是（ ）
    A、m>0 ， n<0 B、m>1 ， n<2 C、m>1 ， n<0 D、m>−2 ， n<−4

    查看试题解析

  • 8. 已知点M（3，－1）关于y轴对称的的对称点N的坐标为（a＋b，1－b），则ab的值为（   ）
    A、10 B、25 C、－3 D、32

    查看试题解析

  • 9. 已知点A（2，a），B（b ， -3）是平面直角坐标系上的两个点，AB∥x轴，且点B在点A的右侧，若AB=5，则（ ）
    A、a=﹣3，b=7 B、a=﹣3，b=﹣3 C、a=2，b=2 D、a=﹣8，b=2

    查看试题解析

  • 10. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断地移动，每次移动一个单位，得到点A1(0 ， 1)、A2(1 ， 1)、A3(1 ， 0)、A4(2 ， 0) ， 那么点A2023的坐标为（ ）

    A、(1011 ， 0) B、(1011 ， 1) C、(2022 ， 0) D、(2022 ， 1)

    查看试题解析

二、填空题（每题2分，共12分）

  • 11. 若(2m+1 ， 2)是第二象限内一点，向右平移2个单位后再向下平移3个单位，该点运动到第四象限，则m的取值范围是.

    查看试题解析

  • 12. 如表是一组密码的一部分，目前已破译出“守初心”的对应口令是“担使命”，根据上述破译方法，破译出“找差距”的对应口令是.

    落

    市

    担

    山

    七

    牢

    七

    中

    湖

    为

    就

    吴

    命

    金

    使

    差

    圾

    守

    立

    实

    华

    人

    忘

    兴

    水

    分

    是

    心

    抓

    初

    成

    民

    银

    垃

    距

    共

    青

    祝

    区

    类

    年

    记

    庆

    找

    周

    和

    国

    州

    绿

    查看试题解析

  • 13. 在平面直角坐标系中，点A(−4 ， 0) ， 点B(4 ， 0)。点C是y轴上一点，满足∠CAB=45°。点E(m ， n)在射线AC上(不与点A重合)，在y轴上存在一点D使得DE=DB ， 若m⋅n=2 ， 求mn+nm=.

    查看试题解析

  • 14. 已知平面上有三个点，点A(2，0)，B(5，2)，C(3，4)，以点A，点B，点C为顶点画平行四边形，则第四个顶点D的坐标为。

    查看试题解析

  • 15. 在平面直角坐标系中，点P(2，3)与点Q(-2 ， m+1)关于原点对称，则m= ．

    查看试题解析

  • 16. 如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，0），（0，1），（﹣1，0）.一个电动玩具从坐标原点O出发，第一次跳跃到点P1.使得点P1与点O关于点A成中心对称；第二次跳跃到点P2 ， 使得点P2与点P1关于点B成中心对称；第三次跳跃到点P3 ， 使得点P3与点P2关于点C成中心对称；第四次跳跃到点P4 ， 使得点P4与点P3关于点A成中心对称；第五次跳跃到点P5 ， 使得点P5与点P4关于点B成中心对称；…照此规律重复下去，则点 P2020 的坐标为.

    查看试题解析

三、作图题（共2题，共17分）

  • 17. 如图所示，在平面直角坐标系中，已知A（0，1），B（2，0），C（4，3）．

    (1)、在平面直角坐标系中画出△ABC ， 以及与△ABC关于y轴对称的△DEF；
    (2)、△ABC的面积是；
    (3)、已知P为y轴上一点，若△ABP的面积为4，求点P的坐标．

    查看试题解析

  • 18. 在如图所示的平面直角坐标系中，已知A(0，1)，B(2，0)，C(3，5).

    (1)、画出△ABC，△A1B1C1 ， 使△A1B1C1与△ABC关于y轴对称；
    (2)、△ABC的面积是；
    (3)、若点P是y轴上一动点，则BP+CP的最小值是.此时P点坐标为

    查看试题解析

四、解答题（共9题，共71分）

  • 19. 如图所示，在平面直角坐标系中，点O为坐标原点，点A的坐标为(2 ， 3).

    (1)、将点A向右平移1个单位，向下平移2个单位所得的点B的坐标为；
    (2)、点A关于y轴的对称点C的坐标为；
    (3)、在平面直角坐标系中标出点B，C所在位置，并求出四边形OBAC的面积.

    查看试题解析

  • 20. 在平面直角坐标系中，O为坐标原点，点A（−4，4−5a）位于第二象限，点B（−4，−a−1）位于第三象限，且a为整数．
    (1)、求点A和点B的坐标．
    (2)、若点C（m ， 0）为x轴上一点，且△ABC是以BC为底的等腰三角形，求m的值．

    查看试题解析

  • 21. 已知点P（x ， y）的坐标满足方程组{x+y−a=0x−y=3a+2 ， 点P在第三象限．
    (1)、请用含a的代表式表示x；
    (2)、请求出a的取值范围．

    查看试题解析

  • 22. 定义：已知平面上两点A(x1 ， y1) ， B(x2 ， y2) ， 称d(A ， B)=|x1−x2|+|y1−y2|为A，B两点之间的折线距离．例如点M(2 ， −3)与点N(5 ， 2)之间的折线距离为d(M ， N)=|2−5|+|−3−2|=3+5=8 ． 如图，已知平面直角坐标系中点A(2 ， 1) ， B(−1 ， 0) ．

    (1)、d(A ， B)=；
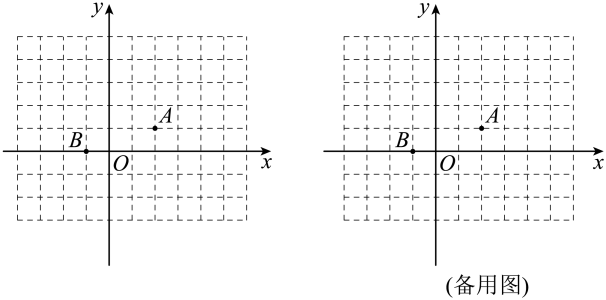    (2)、过点B作直线l平行于y轴，求直线l上与点A的折线距离为5的点的坐标；
    (3)、已知点N(n ， n) ， 且d(A ， N)<2 ， 求n的取值范围；
    (4)、已知平面上点P与原点O的折线距离为3，即d(P ， O)=3 ， 直接写出所有满足条件的点P围成的图形面积．

    查看试题解析

  • 23. 在直角坐标系xOy中，如图1，A ， B点的坐标为(0 ， 4) ， (−4 ， 0) ， P点坐标为(0 ， m) ， 点E是射线BO上的动点，满足BE=1.5OP ， 以PE ， EO为邻边作▱PEOQ ．

    (1)、当m=2时，求出PE的长度；
    (2)、当m>0时，是否存在m的值，使得▱PEOQ的面积等于△ABO面积的14 ， 若存在，求出m的值；若不存在，请说明理由；
    (3)、当点Q在第四象限时，点Q关于E点的对称点为Q' ， 点Q'刚好落在直线AB上时，求m的值(直接写出答案) ．

    查看试题解析

  • 24. 如图，点O是坐标原点，四边形OABC是平行四边形，点A的坐标为(14 ， 0) ， 点B的坐标为(18 ， 43).动点P从O出发，沿射线OA方向以每秒2个单位的速度运动，点Q从B出发以每秒1个单位的速度向点C运动，它们同时出发，当点Q到达点C时P点也停止运动.设运动时间为t秒.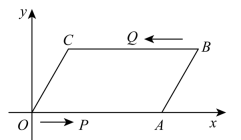

    (1)、写出点C的坐标为；
    (2)、求当t为何值时，以P，Q，A，B为顶点的四边形是平行四边形；
    (3)、在点P，Q运动过程中，连接PQ ，

    ①当t为何值时，使PQ垂直于平行四边形OABC的某一边.

    ②若点C关于PQ的对称点C'恰好落在x轴上，则点Q的坐标为      ▲      .

    查看试题解析

  • 25. 对于平面直角坐标中的任意两点P，Q，若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和，则称P，Q两点为“和合点”，如图1中的P，Q两点即为“和合点”．

    (1)、已知点A(−4 ， 8) ， B(6 ， 0) ， C(6 ， 6) ， D(−2 ， 9) ．

    ①在上面四点中，与点E(−5 ， −7)为“和合点”的是      ▲      ；

    ②若点F(−3 ， 0) ， 过点F作直线l⊥x轴，点G直线l上，A、G两点为“和合点”，则点G的坐标为      ▲      ；

    ③若点M(2a ， 3b)在第二象限，点N(−3a ， −b)在第四象限，且A、M两点为“和合点”，D、N两点为“和合点”，求a，b的值．

    (2)、如图2，已知点H(−5 ， 0) ， K(0 ， 5) ， 点R(x ， y)是线段HK上的一动点，且满足x−y=−5 ， 过点T(n ， 0)作直线m⊥x轴，若在直线m上存在点S，使得R，S两点为“和合点”，直接写出n的取值范围．

    查看试题解析

  • 26. 定义：在平面直角坐标系中，过点P，Q分别作x轴，y轴的垂线所围成的矩形，叫做P，Q的“关联矩形”，如图所示．

    (1)、已知点A(−2 ， 0)

    ①若点B的坐标为(3 ， 2) ， 则点A，B的“关联矩形”的周长为                ．

    ②若点C在直线y=4上，且点A，C的“关联矩形”为正方形，求直线AC的解析式．

    (2)、已知点M(1 ， −2) ， 点N(4 ， 3) ， 若使函数y=kx的图象与点M，N的“关联矩形”有公共点，求k的取值范围．

    查看试题解析

  • 27. 如图，已知二次函数图象顶点为C（1，0），直线y=x+m与该二次函数交于A，B两点，其中A点（3，4），B点在y轴上，

    (1)、求m值及这个二次函数关系式。
    (2)、若点P是对称轴DC上的一个动点，点M的坐标为（0，2），则在x轴上是否存在一点N，使四边形BNPM的周长最小，若存在，求出这个最小值及点P，N的坐标，若不存在，请说明理由。
    (3)、若点P为直线AB上一动点（P不与A，B重合），过P做x轴垂线与二次函数交于点E，①设线段PE长为h，点P横坐标为x，求点P在线段AB上运动时h与x之间的函数关系式，并写出自变量x取值范围。②D为AB与二次函数对称轴的的交点，在直线AB上是否存在点P，使得以点D、C、E、P为顶点的四边形是平行四边形？若存在，请求出P点坐标；若不存在，请说明理由。

    查看试题解析