备考2024年浙江中考数学一轮复习专题28.1锐角三角函数基础夯实

试卷更新日期：2024-03-03 类型：一轮复习

进入出卷网下载

一、选择题（每题2分，共20分）

1. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ，则（）

A、 $\sin A = \frac{3}{4}$ B、 $\cos A = \frac{4}{5}$ C、 $\cos B = \frac{3}{4}$ D、 $\tan B = \frac{3}{5}$

查看试题解析
2. 已知 $\frac{\sqrt{3}}{2}$ ＜cosA＜sin80°，则锐角A的取值范围是（　　）

A、60°＜A＜80° B、30°＜A＜80° C、10°＜A＜60° D、10°＜A＜30°

查看试题解析
3. 在 $△ A B C$ 中， $∠ C = 90^{°}$ ，若 $A C = 3 ， A B = 4$ ，则（）.

A、 $B C = 5$ B、 $\sin A > \tan B$ C、 $\cos A = \frac{3}{4}$ D、 $\tan A = \cos B$

查看试题解析
4. 在 $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $cos A = \frac{3}{5}$ ，那么 $sin A$ 的值等于（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
5. 在△ABC中，∠C=90°，如果tanA= $\frac{3}{4}$ ，那么sinB的值等于（）

A、 $\frac{5}{3}$ B、 $\frac{3}{5}$ C、 $\frac{5}{4}$ D、 $\frac{4}{5}$

查看试题解析
6. 正比例函数y=kx的图象经过点（3，2），则它与x轴所夹锐角的正弦值是（　　）

A、 $\frac{2}{3}$ B、 $\frac{2 \sqrt{13}}{13}$ C、 $\frac{\sqrt{13}}{2}$ D、 $\frac{3 \sqrt{13}}{13}$

查看试题解析
7.
如图，在菱形ABCD中，AE⊥BC于点E，EC=4， $\sin B = \frac{4}{5}$ ，则菱形的周长是（　　）

A、10 B、20 C、40 D、28

查看试题解析
8. 如图，在扇形 $A O B$ 中， $∠ A O B = 90 °$ ，半径 $O A = 3$ ，将扇形 $A O B$ 沿过点 $B$ 的直线折叠，使点 $O$ 恰好落在 $A B$ 上的点 $D$ 处，折痕为 $B C$ ，则阴影部分的面积为（）

A、 $\frac{3 π - 3 \sqrt{3}}{2}$ B、 $\frac{9 π}{4} - 3 \sqrt{3}$ C、 $\frac{π - 3}{4}$ D、 $\frac{3 π - 3}{4}$

查看试题解析
9. 如图，以O为圆心，半径为1的弧交坐标轴于A ， B两点，M是上一点 $($ 不与A ， B重合 $)$ ，连接OM ，设∠MOB=α，则点M的坐标为（）．

A、(sinα ， cosα) B、(cosα ， sinα) C、(cosα ， cosα) D、(sinα ， sinα)

查看试题解析
10. 如图，商用手扶梯 $A B$ 的坡比为 $1 ： \sqrt{3}$ ，已知扶梯的长 $A B$ 为12米，则小明乘坐扶梯从 $B$ 处到 $A$ 处上升的高度 $A C$ 为（）

A、6米 B、 $6 \sqrt{3}$ 米 C、12米 D、 $12 \sqrt{3}$ 米

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，在扇形EOF中放置有三个全等的矩形方格，点O为扇形的圆心，格点A、B、C分别在扇形的两条半径和弧上，已知每个矩形方格的长和宽分别为 $\sqrt{3}$ 和1，则阴影部分的面积为.

查看试题解析
12. 直角三角形的两条直角边长分别为6和8，那么这个三角形的内切圆半径为．

查看试题解析
13. 如图，一辆小汽车在公路l上由东向西行驶，已知测速探头M到公路l的距离MN为9米，测得此车从点A行驶到点B所用的时间为0.6秒，并测得点A的俯角为30^o ，点B的俯角为60^o.那么此车从A到B的平均速度为米/秒.（结果保留三个有效数字，参考数据： $\sqrt{3}$ ≈1.732， $\sqrt{2}$ ≈1.414）

查看试题解析
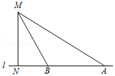14. 如图，要拧开一个边长a=18mm的六角形螺帽，扳手张开的开口b至少要mm..

查看试题解析
15. 图1是一种儿童可折叠滑板车，该滑板车完全展开后示意图如图2所示，由车架 $A B - C E - E F$ 和两个大小相同的车轮组成，已知 $C D = 20 c m ， D E = 15 c m ， s i n ∠ A C D = \frac{4}{5}$ ，当 $A ， E ， F$ 在同一水平高度上时， $∠ C E F = 135 °$ ，则 $A C =$ $c m$ ；为方便存放，将车架前部分绕着点 $D$ 旋转至 $A B ∥ E F$ ，如图3所示，则 $d_{1} - d_{2}$ 为 $c m$ ．

查看试题解析
16. 如图是一种手机三脚架，它通过改变锁扣C在主轴AB上的位置调节三脚架的高度，其它支架长度固定不变，已知支脚DE=AB ．底座CD⊥AB ， BG⊥AB ，且CD=BG ， F是DE上的固定点，且EF：DF=2：3．

(1)、当点B ， G ， E三点在同一直线上（如图1所示）时，测得tan∠BED=2；设BC=5a ，则FG=(用含a的代数式表示)；

(2)、在(1)的条件下，若将点C向下移动24cm，则点B ， G ， F三点在同一直线上（如图2），此时点A离地面的高度是cm．

查看试题解析

三、计算题（共6分）

17.

(1)、 $6 t a n^{2} 30 ° - \sqrt{3} s i n 60 ° - 2 s i n 45 °$

(2)、 $\sqrt{8} - 2 s i n 30 ° + 2 c o s 60 ° + {(\frac{1}{2})}^{- 1}$

查看试题解析

四、作图题（共6分）

18. 如图，在 $6 \times 6$ 的方格纸中，线段 $A B$ 的端点均是格点，请按要求画图．

(1)、在图1中，找一个格点 $P$ ，使得 $△ A B P$ 为直角三角形，且 $∠ A P B \neq 90 °$ ．

(2)、在图2中，找一个格点 $Q$ ，使得 $△ A B Q$ 为非直角三角形，且 $\tan ∠ A Q B = \frac{1}{2}$ ．

查看试题解析

五、解答题（共7题，共42分）

19. 如图，在平面直角坐标系中，△CBO的外接圆⊙M与y轴交于点A（0， $\sqrt{2}$ ），∠C＝60°，∠COB＝45°．

(1)、求OB的长．

(2)、求OC的长．

查看试题解析
20. 如图，在路边安装路灯，灯柱BC高10m，与灯杆AB的夹角ABC为 $6 0^{°}$ .路灯采用锥形灯罩，照射范围DE长为9.8m，从D、E两处测得路灯 $A$ 的仰角分别为 $∠ A D E = 80 . 5^{°} ， ∠ A E D = 4 5^{°}$ .
(参考数据： $c o s 80 . 5^{°} \approx 0.2 ， t a n 80 . 5^{°} \approx 6.0$ )求：

(1)、路灯 $A$ 离地面的高度(即点 $A$ 到地面CE的距离)；

(2)、灯杆AB的长度.

查看试题解析
21. 如图， $△ A B C$ 是直角三角形， $∠ A C B = 90 °$ ，点 $D$ 是 $A C$ 边上一点，以 $A D$ 为直径作 $⊙ O$ 交 $A B$ 边于点 $E$ ，连接 $C E 、 D E$ ，且 $C B = C E$ ．

(1)、求证：直线 $C E$ 是 $⊙ O$ 的切线；

(2)、若 $A D = 15 ， t a n ∠ C E D = \frac{1}{2}$ ，求 $C B$ 的长．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D，E，F分别为 $A B$ ， $A C$ 的中点，G为边 $B C$ 上一点， $∠ E G B = ∠ F D C$ ，连结 $E F$ ．

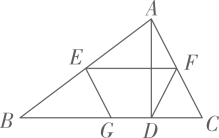(1)、求证：四边形 $E F C G$ 是平行四边形．

(2)、若 $t a n B = \frac{4}{5}$ ， $t a n C = 2$ ， $B C = 14$ ，求 $G D$ 的长．

查看试题解析
23. 如图，某建筑物BC上有一旗杆AB，小明在F处，由E观察到旗杆顶部A的仰角为52°，底部B的仰角为45°，小明的观测点与地面距离EF为1.6m，

(1)、若F与BC相距12m，求建筑物BC的高度；

(2)、若旗杆AB长3.15m，求建筑物BC的高度．（结果精确到0.1m）（参考数据： $\sqrt{2} \approx 1.414 ， s i n 5 2^{\circ} \approx 0.788$ .788，tan52°≈1.280).

查看试题解析
24. 一酒精消毒瓶如图1，AB为喷嘴，△BCD为按压柄，CE为伸缩连杆，BE和EF为导管，其示意图如图2，∠DBE＝∠BEF＝108°，BD＝6cm，BE＝4cm．当按压柄△BCD按压到底时，BD转动到BD′，此时BD′∥EF（如图3）．

(1)、求点D转动到点D′的路径长；

(2)、求点D到直线EF的距离（结果精确到0.1cm）．
（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）

查看试题解析
25. 图1是小明在健身器材上进行仰卧起坐锻炼时情景.
图2是小明锻炼时上半身由EM位置运动到与地面垂直的EN位置时的示意图.

已知BC＝0.64米，AD＝0.24米，AB＝1.30米.

(1)、求AB的倾斜角α的度数（精确到x）；

(2)、若测得EN＝0.85米，试计算小明头顶由M点运动到N点的路径 $\overset{⌢}{M N}$ 的长度.（精确到0.01米）

查看试题解析

六、实践探究题（共2题，共28分）

26. 为了充分利用四边形余料，小明设计了不同的方案裁剪正方形，裁剪方案与数据如表：
方案设计
方案1
方案2
裁剪方案示意图
说明
图中的正方形AEFG和正方形MNPO四个顶点都在原四边形的边上
测量数据
AD=9dm，CD=2dm，AB=14dm，∠A=∠D=90°；

(1)、任务1：探寻边角填空：BC=dm；sinB=；

(2)、任务2：比较面积计算或推理：正方形AEFG和正方形MNP边长之比；

(3)、任务3：应用实践若在△BEF余料上再截取一个最大正方形，正方形的边长为dm.

查看试题解析
27.

(1)、【教材呈现】以下是浙教版八年级下册数学教材第85页的部分内容．先观察图4－17，直线l1∥l2，点A，B在直线l₂上，点C₁ ， C₂ ， C₃ ， C₄在直线l₁上．△ABC₁ ， △ABC₂ ， △ABC₃ ， △ABC₄这些三角形的面积有怎样的关系？请说明理由。

(2)、【基础巩固】如图1，正方形ABCD内接于⊙O，直径MN∥AD，求阴影面积与圆面积的比值；

(3)、【尝试应用】如图2，在半径为5的⊙O中，BD＝CD，∠ACO＝2∠BDO，cos∠BOC＝x，用含x的代数式表示S△ABC；

(4)、【拓展提高】如图3，AB是⊙O的直径，点P是OB上一点，过点P作弦CD⊥AB于点P，点F是⊙O上的点，且满足CF＝CB，连接BF交CD于点E，若BF＝8EP，S△CEF=10 $\sqrt{2}$ ，求⊙O的半径．

查看试题解析

方案设计	方案1	方案2
裁剪方案示意图
说明	图中的正方形AEFG和正方形MNPO四个顶点都在原四边形的边上
测量数据	AD=9dm，CD=2dm，AB=14dm，∠A=∠D=90°；

备考2024年浙江中考数学一轮复习专题28.1锐角三角函数 基础夯实

一、选择题（每题2分，共20分）

二、填空题（每题3分，共18分）

三、计算题（共6分）

四、作图题（共6分）

五、解答题（共7题，共42分）

六、实践探究题（共2题，共28分）

备考2024年浙江中考数学一轮复习专题28.1锐角三角函数基础夯实