备考2024年浙江中考数学一轮复习专题27.1图形的相似基础夯实

试卷更新日期：2024-03-02 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如果 $\frac{b}{a} = \frac{2}{3}$ ，那么 $\frac{a}{a + b} =$ （）

A、 $\frac{3}{2}$ B、 $\frac{2}{5}$ C、 $\frac{5}{3}$ D、 $\frac{3}{5}$

查看试题解析
2. 下列各组数中，成比例的是（）.

A、1，-2，-3，-6 B、1，4，2，-8 C、5，6，2，3 D、 $\sqrt{2}$ ， $\sqrt{6}$ ， 1， $\sqrt{3}$

查看试题解析
3. 下列说法中，不正确的是（）

A、全等图形一定是相似图形 B、直角边长分别是6，4和4.5，3的两个直角三角形相似 C、任意两个矩形都相似 D、三角形的重心分每一条中线成1：2的两条线段

查看试题解析
4. 两个相似三角形一组对应边上的中线长分别是 $2 c m$ 和 $5 c m$ ，且其中较大三角形的周长是 $10 c m$ ，则较小三角形的周长为（）

A、 $4 c m$ B、 $6 c m$ C、 $20 c m$ D、 $25 c m$

查看试题解析
5. 若两个三角形的相似比为1：3，则它们的面积比为（）

A、1：3 B、1：9 C、3：1 D、9：1

查看试题解析
6. 如图△ABC中，∠ACB＝90°，AB＝4，AC＝x ， ∠BAC＝α，O为AB中点，若点D为直线BC下方一点，且△BCD与△ABC相似，则下列结论：
①若α＝60°，则AD的最大值为 $2 \sqrt{7}$ ；
②若α＝60°，△ABC∽△CBD ，则OD的长为 $2 \sqrt{3}$ ；
③若α＝45°，BC与OD相交于E ，则点E不一定是△ABD的重心；
④若△ABC∽△BCD ，则当x＝2时，AC+CD取得最大值．其中正确的为（）

A、①③ B、①②④ C、③④ D、①③④

查看试题解析
7. 在学习画线段AB的黄金分割点时，小明先过点B作AB的垂线BC，再取AB的中点M，以点B为圆心，BM为半径画弧交射线BC于点D，连接AD，再以点D为圆心，DB为半径画弧，前后所画的两弧分别与AD交于E，F两点，最后，以A为圆心，“▗▗”的长度为半径画弧交AB于点H，点H即为AB的其中一个黄金分割点，这里的“▗▗”指的是线段（）

A、AF B、DF C、AE D、DE

查看试题解析
8.
如图，已知E（﹣4，2），F（﹣1，﹣1），以原点O为位似中心，按比例尺2：1把△EFO缩小，则E点对应点E′的坐标为（　　）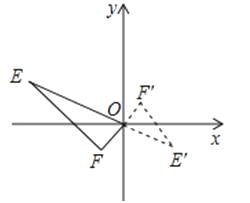

A、（2，1） B、（ $\frac{1}{2}$ ， $\frac{1}{2}$ ） C、（2，﹣1） D、（2，﹣ $\frac{1}{2}$ ）

查看试题解析
9. 如图，在△ABC $A B C$ 纸板中，AC=4，BC=8，AB=10，P是BC上一点，沿过点P $P$ 的直线剪下一个与△ABC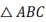相似的小三角形纸板．针对CP $C P$ 的不同取值，三人的说法如下．下列判断正确的是（）
甲：若CP=4， $C P = 4$ 则有3 $3$ 种不同的剪法；乙：若CP=2， $C P = 2$ 则有4 $4$ 种不同的剪法；
丙：若CP=1， $C P = 1$ 则有3 $3$ 种不同的剪法．

A、只有甲错 B、只有乙错 C、只有丙错 D、甲、乙、丙都对

查看试题解析
10. 凸透镜成像的原理如因所示， $A D / / l / / B C$ .若物体到焦点的距离与焦点到凸透镜中心线DB的弫离之比为5：4，则物体被缩小到原来的（）

A、 $\frac{4}{5}$ B、 $\frac{2}{5}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析

二、填空题（每题4分，共24分）

11. 已知 $\frac{x + y}{x - y} = \frac{4}{3}$ ，则 $\frac{x}{y} =$ .

查看试题解析
12. 已知线段 $a = 3$ ， $b = 4$ ，则 $a ， b$ 的比例中项线段等于．

查看试题解析
13. 如图，在 $△ A B C$ 中，D、E分别是 $A B$ 和 $B C$ 上的点，且 $D E ∥ A C$ ， $\frac{A B}{B E} = \frac{A C}{E C}$ ， $\frac{A B}{A C} = \frac{7}{4}$ ，则 $\frac{A B}{B D} =$ ．

查看试题解析
14. 如图，矩形ABCD中，AB＝2，BC＝4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为.

查看试题解析
15. 如图，将正方形ABCD的边AB，BC绕着点A逆时针旋转一定角度，得到线段 $A B^{'}$ ， $B^{^{'}} C^{^{'}}$ ，连接 $A C^{'}$ 交CD于点E，连接 $B B^{'}$ ， $C C^{'}$ ，若 $△ A B B^{'} ∽ △ C E C^{'}$ ，则 $∠ A B B^{'} =$ .

查看试题解析
16. 如图，点P在△ABC的边AC上，请添加一个条件，使△ABP∽△ACB，

查看试题解析

三、作图题(共2题，共12分）

17. 如图是4×4的正方形网格，△ABC的三个顶点均在格点上

(1)、将△ABC绕点A顺时针方向旋转90°得到△AB₁C₁ ，在图①中作出△AB₁C₁；

(2)、在图②中作格点△A₂B₂C₂ ，使△A₂B₂C₂∽△ABC，且周长比为 $\sqrt{2}$ .

查看试题解析
18. 图1、图2均是8×8的正方形网格，每个小正方形的顶点称为格点，线段AB，CD，MN的端点均在格点上，BC与AD相交于点E，回答下列问题：

(1)、在图1中， $t a n ∠ D A B =$ ， $\frac{Δ A B E 的周长}{Δ C D E 的周长} =$ .

(2)、在图2中请用一把无刻度的尺子，画出线段MN三等分点P，Q．（保留作图痕迹）

查看试题解析

四、解答题（共3题，共22分）

19. 已知：线段 $a ， b ， c$ ，且 $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ．

(1)、求 $\frac{a + b}{b}$ 的值；

(2)、如果线段 $a ， b ， c$ ，满足 $a + b + c = 36$ ，求 $a ， b ， c$ 的值．

查看试题解析
20. 如图，矩形 $A B C D$ 中， $B C < 2 A B$ ，点M是 $B C$ 的中点，连接 $A M$ ．将 $△ A B M$ 沿着 $A M$ 折叠后得 $△ A P M$ ，延长 $A P$ 交 $C D$ 于E ，连接 $M E$ ．

(1)、求证： $M E$ 平分 $∠ P M C$ ；

(2)、求证：△EMC∽△MAB.

查看试题解析
21. 学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．

(1)、小丽先调整自己的位置至点P，将直角三角形纸板的三个顶点位置记为A、B、C（如图①），斜边AB平行于地面MN（点M、P、E、N在一直线上），且点D在边AC（较长直角边）的延长线上，此时测得边AB距离地面的高度EF为1.5米，小丽与古树的距离AF为16米，求古树的高度DE；

(2)、为了尝试不同的思路，小丽又向前移动自己的位置至点Q，将直角三角形纸板的三个顶点的新位置记为A′、B′、C′（如图②），使直角边B′C′（较短直角边）平行于地面MN（点M、Q、E、N在一直线上），点D在斜边B′A′的延长线上，且测得此时边B′C′距离地面的高度依然是1.5米，那么小丽向前移动了多少米？

查看试题解析

五、实践探究题（共3题，共32分）

22. 如图

(1)、【基础巩固】如图1，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 60 °$ ，点D是AC的中点．延长BC至点E，使 $D E = D B$ ，延长ED交AB于点F，则 $\frac{A F}{A B}$ 的值为．

(2)、【思考探究】如图2，当 $∠ B A C \neq 60 °$ 时， $\frac{A F}{A B}$ 的值会发生变化吗？若不变，请写出证明过程；若发生变化，请说明理由．

(3)、【拓展延伸】如图3，在 $△ A B C$ 中， $A B = A C$ ，点D是线段AC上任意一点．延长BC至点E，使 $D E = D B$ ，延长ED交AB于点F，若 $\frac{A D}{D C} = n$ ，请求出 $\frac{A F}{A B}$ 的值（用含n的式子表示）．

查看试题解析

23. 根据以下素材，探索完成任务．

素材1	定义：如图1，点 $G$ 将线段 $A D$ 分成两部分，如果 $\frac{A G}{G D} = \frac{G D}{A D}$ ，那么点 $G$ 称为线段 $A D$ 的黄金分割点．
素材2	某兴趣小组在进行研究性学习时，由黄金分割点联想到“黄金分割线”，类似地给出黄金分割线的定义：直线 $l$ 将一个面积为 $S$ 的图形分成面积分别为 $S_{1}$ ， $S_{2}$ 的两部分，如果 $\frac{S_{1}}{S_{2}} = \frac{S_{2}}{S}$ ，那么直线 $l$ 称为该图形的黄金分割线．
素材3	平行四边形是中心对称图形：在同一平面内，一个三角形绕其中一边的中点旋转 $180 °$ ，其余两边与旋转后相对应的两边组成一个平行四边形，例如，图2中的 $△ A B D$ 绕 $B D$ 的中点旋转 $180 °$ 后与原三角形组成一个平行四边形 $A B C D$ （如图3）．

	问题解决
任务1	问题1：如图3， $A D$ 边上黄金分割点 $G$ 旋转后的对称点 $H$ 是否也是 $B C$ 边上的黄金分割点？请写出你的判断结论，并说明理由．问题2：直线 $G H$ 是不是四边形 $A B C D$ 的黄金分割线？请写出你的判断结论：．
任务2	请在图3探索： $B C$ 边上是否存在点 $M$ ，使得直线 $G M$ 是四边形 $A B C D$ 的黄金分割线？如果存在，请说明点 $M$ 的位置；如果不存在，请说明理由．
任务3	兴趣小组探索图2时猜想：在 $△ A B D$ 中，若点 $G$ 为 $A D$ 边上的黄金分割点，连接 $B G$ ，则直线 $B G$ 是 $△ A B D$ 的黄金分割线，你认为对吗？为什么？
任务4	兴趣小组探索图2时还发现：若点 $G$ 是 $△ A B D$ 的边 $A D$ 的黄金分割点，过点 $B$ 任意作一条直线交 $G D$ 于点 $E$ ，再过点 $G$ 作 $G F / / B E$ 交 $A B$ 于点 $F$ ，则直线 $E F$ 是 $△ A B D$ 的黄金分割线，请你给出证明．

查看试题解析

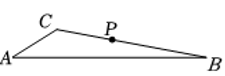
24. 定义：按螺旋式分别延长n边形的n条边至一点，若顺次连接这些点所得的图形与原多边形相似，则称它为原图形的螺旋相似图形.例如：如图1，分别延长多边形A₁A₂…A_n的边得A₁′，A₂′，…，A_n′，若多边形A₁′A₂′…A_n′与多边形A₁A₂…An相似，则多边形A₁′A₂′…A_n′就是A₁A₂…A_n的螺旋相似图形.

(1)、如图2，已知△ABC是等边三角形，作出△ABC的一个螺旋相似图形，简述作法，并给以证明.

(2)、如图3，已知矩形ABCD，请探索矩形ABCD是否存在螺旋相似图形，若存在，求出此时AB与BC的比值；若不存在，说明理由.

(3)、如图4，△ABC是等腰直角三角形，AC＝BC＝2，分别延长CA，AB，BC至A′，B′，C′，使△A′B′C′是△ABC的螺旋相似三角形.若AA′＝kAC，请直接写出BB′，CC′的长（用含k的代数式表示）

查看试题解析

备考2024年浙江中考数学一轮复习专题27.1图形的相似 基础夯实

一、选择题（每题3分，共30分）

二、填空题（每题4分， 共24分）

三、作图题(共2题，共12分）

四、解答题（共3题，共22分）

五、实践探究题（共3题，共32分）

备考2024年浙江中考数学一轮复习专题27.1图形的相似基础夯实

二、填空题（每题4分，共24分）