备考2024年浙江中考数学一轮复习专题27.2图形的相似 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为 , 把△ABO缩小,则点A的对应点A′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)2. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )
 A、 B、 C、 D、3. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1.则CE的长是( )
A、 B、 C、 D、3. 如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形BAE,顶点E恰好落在CD边上,若AD=1.则CE的长是( ) A、 B、 C、2 D、14. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
A、 B、 C、2 D、14. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( ) A、 B、 C、10 D、5. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、 B、 C、10 D、5. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、26. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )
A、 B、1 C、 D、26. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )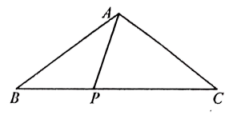 A、或5 B、或 C、或2 D、或27. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )
A、或5 B、或 C、或2 D、或27. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )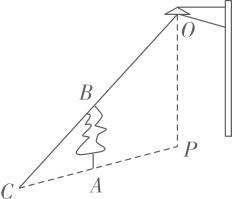 A、3 B、4 C、5 D、68. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( )
A、3 B、4 C、5 D、68. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( ) A、的面积 B、的面积 C、的面积 D、的面积9. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )
A、的面积 B、的面积 C、的面积 D、的面积9. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )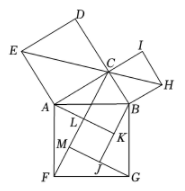 A、 B、 C、 D、10. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )
A、 B、 C、 D、10. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )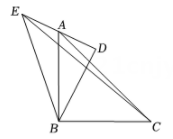 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题(每空3分,共24分)
-
11. 已知 ,则 的值是 .12.
如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为
 13. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .
13. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .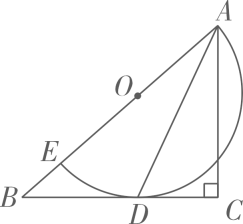 14. 某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A , 再用皮尺分别测量BF , DF , EF , 观测者目高(CD)的长,利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D , EF⊥BD于点F , AB⊥BD于点B , BF=6米,DF=2米,EF=0.5米,CD=1.7米,则这棵树的高度(AB的长)是 米.
14. 某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A , 再用皮尺分别测量BF , DF , EF , 观测者目高(CD)的长,利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D , EF⊥BD于点F , AB⊥BD于点B , BF=6米,DF=2米,EF=0.5米,CD=1.7米,则这棵树的高度(AB的长)是 米.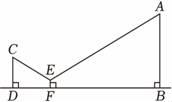 15. 如图,在中, , , 分别是边 , 上的点,且 . 记 , , 的周长分别是 , , .
15. 如图,在中, , , 分别是边 , 上的点,且 . 记 , , 的周长分别是 , , . (1)、若 , 则的值是 .(2)、求的最大值是 .16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,A,B是两侧山脚的入口,从B出发任作线段BC,过C作CD⊥BC,然后依次作垂线段DE,EF,FG,GH,直到接近点A,作AJ⊥GH于点J.每条线段可测量,长度如图所示.分别在BC,AJ上任选点M,N,作MQ⊥BC,NP⊥AJ,使得 , 此时点P,A,B,Q共线.挖隧道时始终能看见P,Q处的标志即可.
(1)、若 , 则的值是 .(2)、求的最大值是 .16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,A,B是两侧山脚的入口,从B出发任作线段BC,过C作CD⊥BC,然后依次作垂线段DE,EF,FG,GH,直到接近点A,作AJ⊥GH于点J.每条线段可测量,长度如图所示.分别在BC,AJ上任选点M,N,作MQ⊥BC,NP⊥AJ,使得 , 此时点P,A,B,Q共线.挖隧道时始终能看见P,Q处的标志即可. (1)、 km.(2)、 = .
(1)、 km.(2)、 = .三、作图题(共9分)
-
17. 如图在5×5的网格中,△ABC的顶点都在格点上.(仅用无刻度的直尺在给定的网格中按要求画图,画图过程用虚线表示,画图结果用实线表示)
 (1)、在图1中画出△ABC的中线AD;(2)、在图2中画线段CE,点E在AB上,使得:=2:3;(3)、在图3中画出△ABC的外心点O.
(1)、在图1中画出△ABC的中线AD;(2)、在图2中画线段CE,点E在AB上,使得:=2:3;(3)、在图3中画出△ABC的外心点O.四、解答题(共5分,共35分)
-
18. 在① , ② , ③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
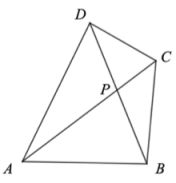
问题:如图,四边形的两条对角线交于P点,若 ▲ (填序号)
求证:.
 19. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 .
19. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 . (1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.20. 如图1,⊙O为锐角三角形ABC的外接圆,点D在BC上,AD交BC于点E,点F在AE上,满足∠AFB-∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连结BD,DG.设∠ACB=α.
(1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.20. 如图1,⊙O为锐角三角形ABC的外接圆,点D在BC上,AD交BC于点E,点F在AE上,满足∠AFB-∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连结BD,DG.设∠ACB=α.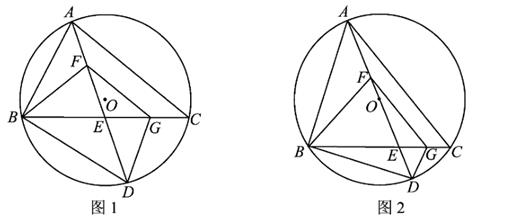 (1)、用含α的代数式表示∠BFD.(2)、求证:△BDE≌△FDG.(3)、如图2,AD为⊙O的直径.
(1)、用含α的代数式表示∠BFD.(2)、求证:△BDE≌△FDG.(3)、如图2,AD为⊙O的直径.①当 的长为2时,求 的长.
②当OF:OE=4:11时,求cosα的值.
21. 如图1,在矩形ABCD中,AB=4,BC=5,动点P从点C出发,以1个单位每秒速度,沿线段CD运动,同时,动点Q从点B出发,以2个单位每秒速度,沿射线BC运动,当点P到达点D时,点P,Q同时停止运动,设运动时间为t秒.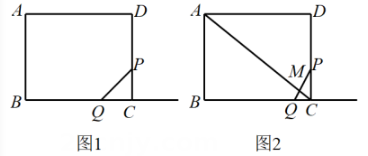 (1)、请用含t的代数式表示线段CQ的长.(2)、如图2,AC与PQ交于点M,当时,求△PMC与△QMC的面积之比.(3)、在点P,Q的整个运动过程中,直线AC上是否存在点E,使以PE为直角边的Rt△PQE,与以点P,Q,C三点为顶点的三角形相似?若不存在,说明理由;若存在,求t的值.22. 如图1,点光源O射出光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像.已知 , 胶片与屏幕的距离为定值,设点光源到胶片的距离长为x(单位:),CD长为y(单位:),当时,.
(1)、请用含t的代数式表示线段CQ的长.(2)、如图2,AC与PQ交于点M,当时,求△PMC与△QMC的面积之比.(3)、在点P,Q的整个运动过程中,直线AC上是否存在点E,使以PE为直角边的Rt△PQE,与以点P,Q,C三点为顶点的三角形相似?若不存在,说明理由;若存在,求t的值.22. 如图1,点光源O射出光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像.已知 , 胶片与屏幕的距离为定值,设点光源到胶片的距离长为x(单位:),CD长为y(单位:),当时,. (1)、求的长.(2)、求y关于x的函数解析式,在图中画出图像,并写出至少一条该函数性质.(3)、若要求不小于 , 求的取值范围.
(1)、求的长.(2)、求y关于x的函数解析式,在图中画出图像,并写出至少一条该函数性质.(3)、若要求不小于 , 求的取值范围.五、实践探究题(共2题,共22分)
-
23.
 (1)、【特例感知】
(1)、【特例感知】如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD , 过点D作DM⊥PD , 交BC的延长线于点M . 求证:△DAP≌△DCM .
(2)、【变式求异】如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB , 交AC于点Q , 点P在边AB的延长线上,连结PQ , 过点Q作QM⊥PQ , 交射线BC于点M . 已知BC=8,AC=10,AD=2DB , 求的值.
(3)、【拓展应用】如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A , C重合),连结PQ , 以Q为顶点作∠PQM=∠PBC , ∠PQM的边QM交射线BC于点M . 若AC=mAB , CQ=nAC(m , n是常数),求的值(用含m , n的代数式表示).
24. 定义:若一个四边形能被其中的一条对角线分割成两个相似三角形,则称这个四边形为“师梅四边形”,这条对角线称为“师梅线”.我们熟知的平行四边形就是“师梅四边形”.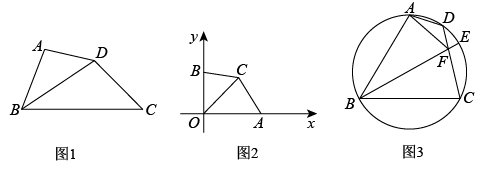 (1)、如图1,平分 , , .四边形是被分割成的“师梅四边形”,求长;(2)、如图2,平面直角坐标系中,A、B分别是x轴和y轴上的点,且 , , 若点C是直线在第一象限上的一点,且是四边形的“师梅线”,求四边形的面积.(3)、如图3,圆内接四边形中,点E是的中点,连接交于点F,连接 , , ①求证:四边形是“师梅四边形”;②若的面积为 , 求线段的长.
(1)、如图1,平分 , , .四边形是被分割成的“师梅四边形”,求长;(2)、如图2,平面直角坐标系中,A、B分别是x轴和y轴上的点,且 , , 若点C是直线在第一象限上的一点,且是四边形的“师梅线”,求四边形的面积.(3)、如图3,圆内接四边形中,点E是的中点,连接交于点F,连接 , , ①求证:四边形是“师梅四边形”;②若的面积为 , 求线段的长.
-