备考2024年浙江中考数学一轮复习专题26.1图形的平移基础夯实

试卷更新日期：2024-03-02 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共36分）

1. 以下现象属于平移的是（）

A、钟摆的摆动 B、电风扇扇叶的转动 C、分针的转动 D、滑雪运动员在平坦的雪地上沿直线滑行

查看试题解析
2. 如图，“宸宸”、“琮琮”、“莲莲”是第十九届亚运会的吉祥物，通过下图平移能得到的是（）

A、 B、 C、 D、

查看试题解析
3. 现实世界中，平移现象无处不在，中国的汉字中有些也可通过平移得到，下列汉字可以看成是通过平移构成的是（）

A、良 B、朋 C、益 D、友

查看试题解析
4. 下列选项的图案中，只要用其中一部分平移一次就可以得到的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，三角形ABC经过平移得到三角形FDE，则下列说法不正确的是（）

A、AB∥FD，AB=FD B、∠ACB=∠FED C、BD=CE D、平移距离为线段CD的长度

查看试题解析
6. 有下列说法：①三角形ABC在平移过程中，对应线段一定相等；②三角形ABC在平移过程中，对应线段一定平行或共线；③三角形ABC在平移过程中，周长不变；④三角形ABC在平移过程中，面积不变．其中正确的说法是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
7. 在Rt△ABC中，∠ABC=90°，AC=13，AB=12，则图中五个小直角三角形的周长之和为（）

A、25 B、18 C、17 D、30

查看试题解析
8. 某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的模型，则所用铁丝的长度关系是（）

A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝-样长

查看试题解析
9. 如图，长方形 $A B C D$ 中， $A B = 3 c m$ ， $B C = 8 c m$ ，现将该长方形沿 $B C$ 方向平移．得到长方形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ ，若重叠部分 $A_{1} B_{1} C D$ 的面积为 $6 c m^{2}$ ，则长方形 $A B C D$ 向右平移的距离为（）

A、 $2 c m$ B、 $6 c m$ C、 $8 c m$ D、 $14 c m$

查看试题解析
10. 如图，在△ABC中，已知AB＝8，点D、E分别在边AC、AB上，现将△ADE沿直线DE折叠，使点A恰好落在点F处，若将线段BC向左平移刚好可以与线段EF重合，连结CF.若2BC+CF＝15，则BC-2CF的值为（）

A、4 B、5 C、6 D、7

查看试题解析
11. 已知M（2，2）.规定“把点M先作关于x轴对称，再向左平移1个单位”为一次变换.那么连续经过2018次变换后，点M的坐标变为（）

A、（﹣2016，2） B、（﹣2016，一2） C、（﹣2017，﹣2） D、（﹣2017，2）

查看试题解析
12. 如图，在平面直角坐标系中，点 $A$ ， $B$ ， $C$ 的坐标分别为 $(4 ， 6)$ ， $(4 ， 0)$ ， $(- 2 ， 3) .$ 将点 $C$ 向右平移 $n$ 个单位后得到点 $C' .$ 若点 $C'$ 落在 $△ A O B$ 内 $($ 包括边界 $)$ ，则 $n$ 的取值范围是（）

A、 $4 \leq n \leq 6$ B、 $4 \leq n \leq 7$ C、 $5 \leq n \leq 6$ D、 $5 \leq n \leq 7$

查看试题解析

二、填空题（每题4分，共24分）

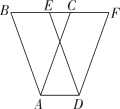
13. 如图所示，在三角形ABC中，BC=6cm．将三角形ABC以每秒2 cm的速度沿BC所在直线向右平移，所得图形对应为三角形DEF，设平移时间为t秒，若要使AD=2CE成立，则t的值为

查看试题解析
14. 计划在一块长为10米，宽为7米的长方形草坪上，修建一条宽为2米的人行道，则剩余草坪的面积为平方米.

查看试题解析
15. 如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝6，DH＝2，平移距离为3，则阴影部分的面积为．

查看试题解析
16. 如图，△ABC的边AB长为4cm ，将△ABC沿着BB′方向平移2cm得到△A'B'C''，且BB'⊥AB，则阴影部分的面积是cm² ．

查看试题解析
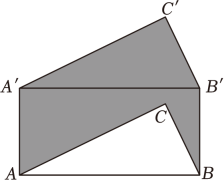17. 已知O、A、B的坐标分别是（0，0），（3，1），（﹣1，2），在平面内找一点M，使得以点O、A、B、M为顶点的四边形是平行四边形，则点M的坐标为．

查看试题解析
18. 如图，在平面直角坐标系中，将正方形①依次平移后得到正方形②，③，④…；相应地，顶点A依次平移得到A₁ ， A₂ ， A₃ ， …，其中A点坐标为（1，0），A₁坐标为（0，1），则A₂₀的坐标为．

查看试题解析

三、作图题（共9分）

19. 如图，在正方形网格中，每个小正方形的边长均为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为 $(- 4 ， 5)$ 、 $(- 1 ， 3)$ .

(1)、请在如图所示的网格平面内画出平面直角坐标系；

(2)、点 $P (m ， n)$ 是 $△ A B C$ 边BC上任意一点，三角形经过平移后得到 $△ A_{1} B_{1} C_{1}$ ，点P的对应点为 $P_{1} (m + 6 ， n - 2)$ .
①直接写出点 $B_{1}$ 的坐标 ▲ ；

②画出 $△ A B C$ 平移后的 $△ A_{1} B_{1} C_{1}$ .

(3)、在y轴上是否存在点P，使 $△ A O P$ 的面积等于 $△ A B C$ 面积的 $\frac{2}{3}$ ，若存在，请求出点P的坐标；若不存在，请说明理由.

查看试题解析

四、解答题（共4题，共39分）

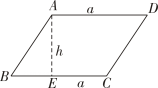
20. 我们知道平行四边形的面积公式S=ah，请你结合图形．利用平移的方法加以说明．

查看试题解析
21. 如图所示，已知射线CB∥OA，∠C= ∠OAB=100°，E，F在CB上，且满足∠FOB=∠AOB，OE平分∠COF．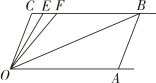

(1)、求∠EOB的度数．(直接写出结果，无须解答过程)

(2)、若在OC右侧左右平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，请找出变化的规律；若不变，请求出这个比值．

(3)、在OC右侧左右平行移动AB的过程中，是否存在使∠OEC=∠OBA的情况？若存在，请直接写出∠OEC度数；若不存在，请说明理由．

查看试题解析
22. 如图1，已知直线PQ∥MN，点A在直线PQ上，点C，D在直线MN．上，连结AC，AD，∠PAC= 50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．

(1)、求∠AEC的度数；

(2)、若将图1中的线段AD沿MN向右平移到A₁D₁如图2所示的位置，此时A₁E平分∠AA₁D₁ ， CE平分∠ACD₁ ， A₁E与CE相交于E，∠PAC=50°，∠A₁D₁C=30，求∠A₁EC的度数；

(3)、若将图1中的线段AD沿MN向左平移到A₁D₁如图3所示的位置，其他条件与(2)相同，求此时∠A₁EC的度数．

查看试题解析
23. 已知大正方形的边长为4cm，小正方形的边．长为2cm，起始状态如图所示．大正方形固定不动，把小正方形以1cm/s的速度沿水平方向向右平移，设平移的时间为1(s)．两个正方形重叠部分的面积为S(cm²)．完成下列问题：

(1)、平移1.5s时，S=cm²

(2)、当2≤t≤4时，小正方形的一条对角线扫过图形的面积为多少？

(3)、当S=2cm²时，小正方形平移的距离为多少厘米？

查看试题解析

五、实践探究题（共12分）

24. 平移是一种基本的几何图形变换，利用平移可将分散的条件相对集中，以达到解决问题的目的.如图1，在四边形 $A B C D$ 中， $A D ∥ B C ， A C ⊥ B D$ ，若 $A C = 3 ， B D = 5$ ，求 $A D + B C$ 的值.
小明发现，平移 $A C$ 至 $D E$ ，构造 $▱ A C E D$ ，经过推理和计算能够使问题得到解决（如图2）.

(1)、【求解体验】
请根据小明的思路求 $A D + B C$ 的值.

(2)、【尝试应用】
如图3，在矩形 $A B C D$ 和 $▱ A B E F$ 中，连结 $D F 、 A E$ 交于点G，连接 $D B$ .若 $A E = D F = D B$ ，求 $∠ F G E$ 的度数；

(3)、【拓展延伸】
如图4，在（2）的条件下，连结 $B F$ ，若 $A B = A D ， F G = 2$ ，求 $△ B D F$ 的面积.

查看试题解析

备考2024年浙江中考数学一轮复习专题26.1图形的平移 基础夯实

一、选择题（每题3分，共36分）

二、填空题（每题4分， 共24分）

三、作图题（共9分）

四、解答题（共4题，共39分）

五、实践探究题（共12分）

备考2024年浙江中考数学一轮复习专题26.1图形的平移基础夯实

二、填空题（每题4分，共24分）