备考2024年浙江中考数学一轮复习专题26.2图形的平移 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 在 方格中,将图 中的图形甲平移后位置如图 所示,则图形甲的平移方法正确的是( )
 A、先向左平移1格,再向下平移2格 B、先向右平移3格,再向下平移2格 C、先向右平移1格,再向下平移3格 D、先向右平移2格,再向下平移3格2. 如图,从图1的正三角形到图2的正三角形,下列变化中不能得到的是( )
A、先向左平移1格,再向下平移2格 B、先向右平移3格,再向下平移2格 C、先向右平移1格,再向下平移3格 D、先向右平移2格,再向下平移3格2. 如图,从图1的正三角形到图2的正三角形,下列变化中不能得到的是( ) A、绕某点旋转 B、平移 C、轴对称 D、先平移再轴对称3. 在平面直角坐标系中,线段 是由线段 经过平移得到的,已知点 的对应点为 ,点B的对应点为 ,则点B的坐标为( )A、 B、 C、 D、4. 已知线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为( )A、(﹣8,﹣2) B、(﹣2,﹣2) C、(2,4) D、(﹣6,﹣1)5. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A、绕某点旋转 B、平移 C、轴对称 D、先平移再轴对称3. 在平面直角坐标系中,线段 是由线段 经过平移得到的,已知点 的对应点为 ,点B的对应点为 ,则点B的坐标为( )A、 B、 C、 D、4. 已知线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为( )A、(﹣8,﹣2) B、(﹣2,﹣2) C、(2,4) D、(﹣6,﹣1)5. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )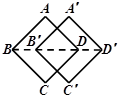 A、1cm B、2cm C、( -1)c. D、(2 -1)cm6. 如图, 中, , , ,平行四边形内放着两个菱形,菱形 和菱形 ,它们的重叠部分是平行四边形 .已知三个阴影平行四边形的周长相等,那么平行四边形 的面积为( )
A、1cm B、2cm C、( -1)c. D、(2 -1)cm6. 如图, 中, , , ,平行四边形内放着两个菱形,菱形 和菱形 ,它们的重叠部分是平行四边形 .已知三个阴影平行四边形的周长相等,那么平行四边形 的面积为( )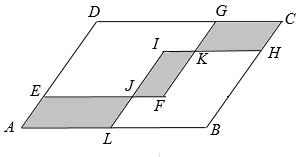 A、 B、 C、 D、7. 如图,直线y x+5交坐标轴于点A、B,与坐标原点构成的△AOB向x轴正方向平移4个单位长度得△A′O′B′,边O′B′与直线AB交于点E,则图中阴影部分面积为( )
A、 B、 C、 D、7. 如图,直线y x+5交坐标轴于点A、B,与坐标原点构成的△AOB向x轴正方向平移4个单位长度得△A′O′B′,边O′B′与直线AB交于点E,则图中阴影部分面积为( ) A、 B、15 C、10 D、148. 如图,将竖直向上平移得到 , 与交于点G,G恰好为的中点.若 , , 则的长为( )
A、 B、15 C、10 D、148. 如图,将竖直向上平移得到 , 与交于点G,G恰好为的中点.若 , , 则的长为( ) A、6 B、 C、 D、89. 如图,△ABC沿直线BC向右平移得到△DEF,已知EC=2,BF=8,则CF的长为( )
A、6 B、 C、 D、89. 如图,△ABC沿直线BC向右平移得到△DEF,已知EC=2,BF=8,则CF的长为( ) A、3 B、4 C、5 D、610. 如图,已知A,B的坐标分别为 , , 将沿x轴正方向平移,使B平移到点E,得到 , 若 , 则点C的坐标为( )
A、3 B、4 C、5 D、610. 如图,已知A,B的坐标分别为 , , 将沿x轴正方向平移,使B平移到点E,得到 , 若 , 则点C的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共32分)
-
11. 如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为米2 .
 12. 如图,在Rt△ABC中, ∠ACB=90°,∠A=30°,BC=2cm .把 △ABC沿AB方向平移1cm,得到△A'B'C' ,连结CC',则四边形AB'C'C 的周长为cm..
12. 如图,在Rt△ABC中, ∠ACB=90°,∠A=30°,BC=2cm .把 △ABC沿AB方向平移1cm,得到△A'B'C' ,连结CC',则四边形AB'C'C 的周长为cm..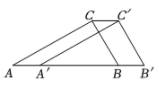 13. 如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,EF=8,BE=3,CB与DF交于点G,CG=3,则图中阴影部分的面积为 .
13. 如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,EF=8,BE=3,CB与DF交于点G,CG=3,则图中阴影部分的面积为 . 14. 如图,在中, , 将平移得到 , 当且经过边的中点D时,四边形的周长为.
14. 如图,在中, , 将平移得到 , 当且经过边的中点D时,四边形的周长为.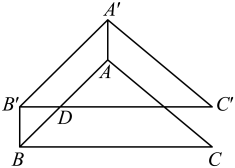 15. 如图,在中, , 将平移5个单位长度得到 , 点、分别是、的中点,的最小值等于.
15. 如图,在中, , 将平移5个单位长度得到 , 点、分别是、的中点,的最小值等于.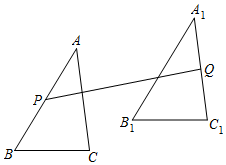 16. 如图,点 , , , 分别是矩形 各边上的中点,将矩形 向右平移得矩形 ,点 , , , 的对应点分别为点 , , , .若 ,矩形 的面积为84,则图中阴影部分的面积为 .
16. 如图,点 , , , 分别是矩形 各边上的中点,将矩形 向右平移得矩形 ,点 , , , 的对应点分别为点 , , , .若 ,矩形 的面积为84,则图中阴影部分的面积为 . 17. 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm,BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1 , 连接AC1 , BD1。当四边形ABD1C1是矩形时,则平移的距离为 cm
17. 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm,BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1 , 连接AC1 , BD1。当四边形ABD1C1是矩形时,则平移的距离为 cm 18. 如图,在平面直角坐标系xOy中,点 A (0,4), B(3,4),将△ABO向右平移到 △CDE 位置, A 的对应点是 C, O的对应点是 E,函数 的图象经过点 C 和DE的中点 F,则k的值是 .
18. 如图,在平面直角坐标系xOy中,点 A (0,4), B(3,4),将△ABO向右平移到 △CDE 位置, A 的对应点是 C, O的对应点是 E,函数 的图象经过点 C 和DE的中点 F,则k的值是 .
三、作图题(共8分)
-
19. 如图,在8×8的方格纸中,P,Q为格点,的顶点均在格点上,请按要求画图.(注:图1,图2在答题卷上.)
 (1)、在图1中画出平移后的格点三角形,使得点B的对应点是线段的中点.(2)、在图2中画出平移后的格点 , 点A,B,C的对应点分别是点D,E,F,满足以下两个条件:
(1)、在图1中画出平移后的格点三角形,使得点B的对应点是线段的中点.(2)、在图2中画出平移后的格点 , 点A,B,C的对应点分别是点D,E,F,满足以下两个条件:①直线经过线段的一个端点;
②三个顶点均不落在线段上.
四、解答题(共2题,共16分)
-
20. 如图,在平面直角坐标系中, ▱ ABCD的顶点D与原点O重合。点C在y轴正半轴上,点B在反比例函数y= (k >1)的图象上,已知CD=2,点A坐标为(2,1).
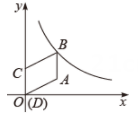 (1)、求k的值.(2)、将 ▱ ABCD沿x轴正方向平移,当A点落在反比例函数图象上时,求平移的距离.21. 如图,抛物线 ,交 轴于点 、 ,交 轴于点 ,已知 的横坐标为 .
(1)、求k的值.(2)、将 ▱ ABCD沿x轴正方向平移,当A点落在反比例函数图象上时,求平移的距离.21. 如图,抛物线 ,交 轴于点 、 ,交 轴于点 ,已知 的横坐标为 . (1)、求点 的坐标. 用含 的代数式表示(2)、抛物线的对称轴交 轴于点 ,连结 ,平移线段 ,使点 与 重合,此时点 恰好落在抛物线上,求 的值.
(1)、求点 的坐标. 用含 的代数式表示(2)、抛物线的对称轴交 轴于点 ,连结 ,平移线段 ,使点 与 重合,此时点 恰好落在抛物线上,求 的值.五、实践探究题(共14分)
-
22. 李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是李老师在“图形的变化”主题下设计的问题,请你解答.(1)、观察发现
如图1,在平面直角坐标系中,过点的直线轴,作关于y轴对称的C图形 , 再分别作关于x轴和直线l对称的图形和 , 则可以看作是绕点O顺时针旋转得到的,旋转角的度数为;可以看作是向右平移得到的,平移距离为个单位长度.
 (2)、探究迁移
(2)、探究迁移如图2,中, , P为直线AB下方一点,作点P关于直线AB的对称点 , 再分别作点关于直线AD和直线CD的对称点和 , 连接AP, , 请仅就图2的情形解决以下问题:


①若 , 请判断β与α的数量关系,并说明理由;
②若 , 求P,两点间的距离.
(3)、拓展应用在(2)的条件下,若 , , , 连接 . 当与的边平行时,请直接写出AP的长.
-