备考2024年浙江中考数学一轮复习专题25.1图形旋转 基础夯实
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题2分,共20分)
-
1. 下列现象属于旋转的是( )A、摩托车在急刹车时向前滑动 B、飞机起飞后冲向空中的时候 C、笔直的铁轨上飞驰而过的火车 D、幸运大转盘转动的过程2.
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列图形中是旋转对称图形但不是中心对称图形的是( )A、
3. 下列图形中是旋转对称图形但不是中心对称图形的是( )A、 B、
B、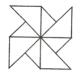 C、
C、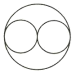 D、
D、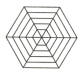 4. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、
4. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、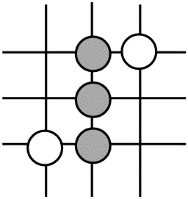
B、
B、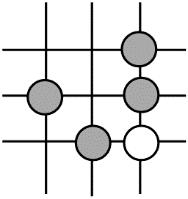
C、
C、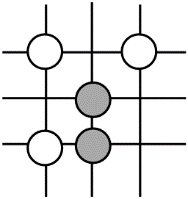
D、
D、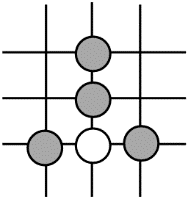
5. 如果规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,就称此图形为旋转对称图形,旋转的角度称为旋转角.下列图形是旋转对称图形,且有一个旋转角为60°的是( )A、正三角形 B、正方形 C、正六边形 D、正八边形6. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )
5. 如果规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,就称此图形为旋转对称图形,旋转的角度称为旋转角.下列图形是旋转对称图形,且有一个旋转角为60°的是( )A、正三角形 B、正方形 C、正六边形 D、正八边形6. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )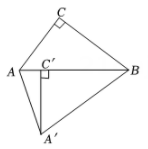 A、 B、4 C、 D、57. 如图,在Rt△ACB中,∠ACB=90°,∠A=35°,将△ABC绕点C逆时针旋转α角到△A1B1C 的位置,A1B1恰好经过点B,则旋转角α的度数等( )
A、 B、4 C、 D、57. 如图,在Rt△ACB中,∠ACB=90°,∠A=35°,将△ABC绕点C逆时针旋转α角到△A1B1C 的位置,A1B1恰好经过点B,则旋转角α的度数等( ) A、70° B、65° C、55° D、35°8. 若点 , 关于原点成中心对称,则a,b的值分别为( )A、 , B、 , C、 , D、 ,9. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A、70° B、65° C、55° D、35°8. 若点 , 关于原点成中心对称,则a,b的值分别为( )A、 , B、 , C、 , D、 ,9. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( ) A、(﹣ ,3) B、(﹣3, ) C、(﹣ ,2+ ) D、(﹣1,2+ )10. 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
A、(﹣ ,3) B、(﹣3, ) C、(﹣ ,2+ ) D、(﹣1,2+ )10. 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( ) A、(﹣4,﹣2﹣ ) B、(﹣4,﹣2+ ) C、(﹣2,﹣2+ ) D、(﹣2,﹣2﹣ )
A、(﹣4,﹣2﹣ ) B、(﹣4,﹣2+ ) C、(﹣2,﹣2+ ) D、(﹣2,﹣2﹣ )二、填空题(每题2分,共12分)
-
11. 分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是度.
 12. 如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为.
12. 如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为. 13. 如图,在Rt△ACB中,∠ACB=90°,∠A=27°,将△ABC绕点C逆时针旋转α角到△A1B1C的位置,A1B1恰好经过点B,则旋转角α的度数是.
13. 如图,在Rt△ACB中,∠ACB=90°,∠A=27°,将△ABC绕点C逆时针旋转α角到△A1B1C的位置,A1B1恰好经过点B,则旋转角α的度数是. 14. 如图是一个中心对称图形,A为对称中心,若 , , ,则 的长为.
14. 如图是一个中心对称图形,A为对称中心,若 , , ,则 的长为.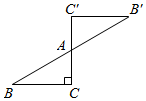 15. 如图,已知点 , , , ,连接 , ,将线段 绕着某一点旋转一定角度,使 , 分别与 , 重合,则旋转中心的坐标为.
15. 如图,已知点 , , , ,连接 , ,将线段 绕着某一点旋转一定角度,使 , 分别与 , 重合,则旋转中心的坐标为.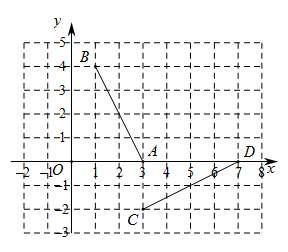 16. 如图,把双曲线绕着原点逆时针旋转与轴交于点 ,
16. 如图,把双曲线绕着原点逆时针旋转与轴交于点 , (1)、若点B(0,2),则k=;(2)、若点A(3,5)在旋转后的曲线上,则k= .
(1)、若点B(0,2),则k=;(2)、若点A(3,5)在旋转后的曲线上,则k= .三、作图题(共3题,共18分)
-
17. 如图,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6)在给出的平面直角坐标系中:
 (1)、画出△ABC绕点A顺时针旋转90°后得到的△AB1C1;并直接写出B1 , C1的坐标;(2)、计算点B旋转到点B1位置时,经过的路径弧BB1的长度.18. 如图,在直角坐标系中,点A,B的坐标分别是A(-1,1),B(-1,3).
(1)、画出△ABC绕点A顺时针旋转90°后得到的△AB1C1;并直接写出B1 , C1的坐标;(2)、计算点B旋转到点B1位置时,经过的路径弧BB1的长度.18. 如图,在直角坐标系中,点A,B的坐标分别是A(-1,1),B(-1,3). (1)、画出△AOB绕点O顺时针旋转90°后所得的图形△A1OB1;(2)、求出此过程中线段BO扫过图形的面积(结果保留π).19. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系.
(1)、画出△AOB绕点O顺时针旋转90°后所得的图形△A1OB1;(2)、求出此过程中线段BO扫过图形的面积(结果保留π).19. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系. (1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1;(2)、写出点A1 , B1的坐标;(3)、求四边形AOA1B1的面积.
(1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1;(2)、写出点A1 , B1的坐标;(3)、求四边形AOA1B1的面积.四、解答题(共8题,共52分)
-
20. 求证:在直角坐标系中,点A(x,y)与点B(-x,-y)关于原点成中心对称.21. 如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
 22. 如图,在Rt△ABC中, , 点P为边上的一点,将线段绕点A顺时针方向旋转(点P对应点).当旋转至时,点恰好在同一直线上,此时作于点E.
22. 如图,在Rt△ABC中, , 点P为边上的一点,将线段绕点A顺时针方向旋转(点P对应点).当旋转至时,点恰好在同一直线上,此时作于点E. (1)、求证:∠CBP=∠ABP;(2)、若AB-BC=4,AC=8,求△PBC的面积;(3)、在(2)的条件下,点N为边上一动点,点M为边上一个动点,连接 , 求的最小值,请直接写出答案.23. 如图1, 已知 ,射线 从 位置出发,以每秒 的速度按顺时针方向向射线 旋转;与此同时, 射线 以每秒 的速度,从 位置出发按逆时针方向向射线 旋转,到达射线 后又以同样的速度按顺时针方向返回,当射线 与射线 重合时,两条射线同时停止运动,设旋转时间为t(s).
(1)、求证:∠CBP=∠ABP;(2)、若AB-BC=4,AC=8,求△PBC的面积;(3)、在(2)的条件下,点N为边上一动点,点M为边上一个动点,连接 , 求的最小值,请直接写出答案.23. 如图1, 已知 ,射线 从 位置出发,以每秒 的速度按顺时针方向向射线 旋转;与此同时, 射线 以每秒 的速度,从 位置出发按逆时针方向向射线 旋转,到达射线 后又以同样的速度按顺时针方向返回,当射线 与射线 重合时,两条射线同时停止运动,设旋转时间为t(s).
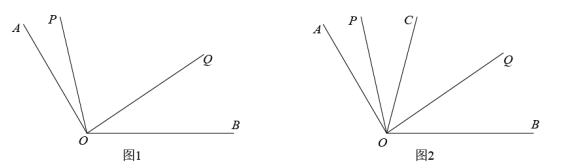 (1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.24. 如图,在平面直角坐标系中,已知点 , 点 , 其中a,b满足 , 点P从点O出发,沿的路径以每秒2个单位的速度向终点A运动,设运动时间为t秒.
(1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.24. 如图,在平面直角坐标系中,已知点 , 点 , 其中a,b满足 , 点P从点O出发,沿的路径以每秒2个单位的速度向终点A运动,设运动时间为t秒.
 (1)、求线段的值.(2)、是否存在t,使得为等腰三角形,若存在,请求出所有t的值,若不存在,请说明理由.(3)、当平分时,求t的值.(4)、线段绕点A按逆时针方向旋转90得到线段 , 连结 , 若该平面内存在点 , 使得与的面积相等,则m的值为.25. 在平面直角坐标系中,已知点 , 点.
(1)、求线段的值.(2)、是否存在t,使得为等腰三角形,若存在,请求出所有t的值,若不存在,请说明理由.(3)、当平分时,求t的值.(4)、线段绕点A按逆时针方向旋转90得到线段 , 连结 , 若该平面内存在点 , 使得与的面积相等,则m的值为.25. 在平面直角坐标系中,已知点 , 点. (1)、若将沿轴向右平移个单位,此时点恰好落在反比例函数的图象上,求的值;(2)、若绕点按逆时针方向旋转度.
(1)、若将沿轴向右平移个单位,此时点恰好落在反比例函数的图象上,求的值;(2)、若绕点按逆时针方向旋转度.①当时,点恰好落在反比例函数图象上,求的值;
②问点能否同时落在(1)中的反比例函数的图象上?若能,直接写出的值;若不能,请说明理由.
26. 定义:在平面直角坐标系中,若两条抛物线的顶点关于原点成中心对称,且二次项系数之积等于﹣2.我们就称其中一条抛物线是另一条抛物线的逆对抛物线.(1)、写出抛物线y=x2+2x﹣3的顶点坐标,并写出它的逆对抛物线;(2)、已知抛物线y2=ax2+bx+c是抛物线y1=mx2+4mx+3m的逆对抛物线.①当抛物线y1经过点(﹣2,﹣1)时,求a+b+c的值;
②设抛物线y1与x轴的两个交点为A,B(点A在点B的左侧),抛物线y2与x轴的交点为C(在其对称轴左侧).若这三点依次排列后,点B恰好是A,C两点连线的中点,求此时m的值.
27. 如图1,△ABC是⊙O内接三角形将△ABC绕点A逆时针旋转至△AED,其中点D在圆上,点E在线段AC上. (1)、求证:DE=DC;(2)、如图2,过点B作BF∥CD分别交AC、AD于点M、N,交⊙O于点F,连结AF.求证:AN·DE=AF·BM:(3)、在(2)的条件下,若时,求的值.
(1)、求证:DE=DC;(2)、如图2,过点B作BF∥CD分别交AC、AD于点M、N,交⊙O于点F,连结AF.求证:AN·DE=AF·BM:(3)、在(2)的条件下,若时,求的值.五、实践探究题(共2题,共18分)
-
28. 如图1,四边形ABCD是正方形,E,F分别在边BC和CD上,且∠EAF=45°,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法。小明为了解决线段EF,BE,DF之间的关系,将△ADF绕点A顺时针旋转90°后解决了这个问题。
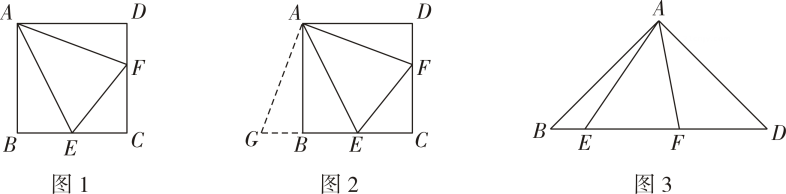 (1)、请直接写出线段EF,BE,DF之间的关系.(2)、如图3,等腰直角三角形ABD,∠BAD=90°,AB=AD,点E,F在边BD上,且∠EAF=45°,请写出EF,BE,DF之间的关系,并说明理由.29. 数学兴趣小组围绕“三角形的内角和是”,进行了一系列探究,过程如下:
(1)、请直接写出线段EF,BE,DF之间的关系.(2)、如图3,等腰直角三角形ABD,∠BAD=90°,AB=AD,点E,F在边BD上,且∠EAF=45°,请写出EF,BE,DF之间的关系,并说明理由.29. 数学兴趣小组围绕“三角形的内角和是”,进行了一系列探究,过程如下: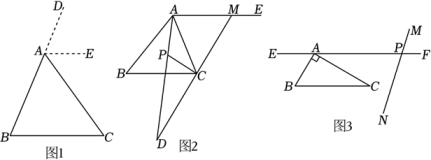 (1)、【论证】如图1,延长至D,过点作 , 就可以说明成立,即:三角形的内角和为 , 请完成上述说理过程.(2)、【应用】如图2,在中,的平分线与的角平分线交于点 , 过点作 , 在射线上,且 , 的延长线与的延长线交于点D.
(1)、【论证】如图1,延长至D,过点作 , 就可以说明成立,即:三角形的内角和为 , 请完成上述说理过程.(2)、【应用】如图2,在中,的平分线与的角平分线交于点 , 过点作 , 在射线上,且 , 的延长线与的延长线交于点D.①求的度数;
②设 , 请用的代数式表示 .
(3)、【拓展】如图3,在中, , , 过点A作 , 直线与相交于A点右侧的点P, . 绕点以每秒的速度顺时针方向旋转,同时绕点以每秒的速度顺时针方向旋转,与重合时再绕着点以原速度逆时针方向旋转,当旋转一周时,运动全部停止,设运动时间为秒,在旋转过程中,是否某一时刻,使得与的一边平行?若存在,求的值;若不存在,请说明理由.