备考2024年浙江中考数学一轮复习专题25.2图形旋转 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( )
2. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( ) A、M1 B、M2 C、M3 D、M43. 如图,在矩形ABCD内放入六个小正方形后形成一个中心对称图形,其中顶点E,F分别在边BC,AD上,则长AD与宽AB的比为( )
A、M1 B、M2 C、M3 D、M43. 如图,在矩形ABCD内放入六个小正方形后形成一个中心对称图形,其中顶点E,F分别在边BC,AD上,则长AD与宽AB的比为( ) A、6:5 B、13:10 C、8:7 D、4:34. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )
A、6:5 B、13:10 C、8:7 D、4:34. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )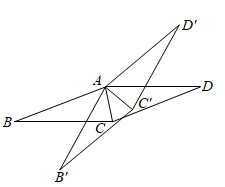 A、 B、 C、 D、5. 如图,中, , 绕点逆时针旋转得到 , 点的对应点是点 , 连接 , 若 , 则旋转角是( )
A、 B、 C、 D、5. 如图,中, , 绕点逆时针旋转得到 , 点的对应点是点 , 连接 , 若 , 则旋转角是( )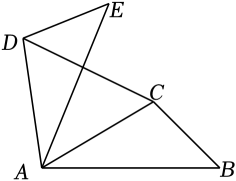 A、 B、 C、 D、6. 如图,将等腰三角形绕点C顺时针旋转得到 , 已知 , , 则的度数为( ).
A、 B、 C、 D、6. 如图,将等腰三角形绕点C顺时针旋转得到 , 已知 , , 则的度数为( ).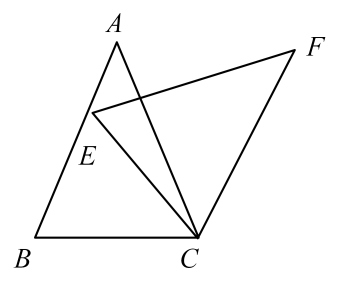 A、 B、 C、 D、7. 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到,点C在边EF上,过点E作AD平行线得矩形ANMD,则要知道矩形ANMD的面积只需知道( )
A、 B、 C、 D、7. 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到,点C在边EF上,过点E作AD平行线得矩形ANMD,则要知道矩形ANMD的面积只需知道( ) A、S△BEC B、S△BGC C、S△ECM D、S△CGF8. 在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形是中心对称图形的概率是( )A、 B、 C、 D、9. 矩形ABCD绕着对角线交点O旋转60°,若重合部分四边形EFGH的面积为矩形ABCD面积的 , 则的比值是( )
A、S△BEC B、S△BGC C、S△ECM D、S△CGF8. 在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形是中心对称图形的概率是( )A、 B、 C、 D、9. 矩形ABCD绕着对角线交点O旋转60°,若重合部分四边形EFGH的面积为矩形ABCD面积的 , 则的比值是( ) A、 B、 C、3 D、10. , AC=1,以BC为边作正方形BCED,当线段AC绕点A任意旋转时,正方形BCED也随之旋转,若x=AD+AE,则x的取值范围是( )
A、 B、 C、3 D、10. , AC=1,以BC为边作正方形BCED,当线段AC绕点A任意旋转时,正方形BCED也随之旋转,若x=AD+AE,则x的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共21分)
-
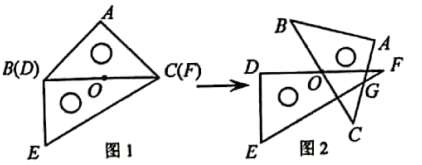
11. 在直角坐标系中,点(4,5)绕原点O逆时针方向旋转90°,得到的点的坐标是.12. 一副三角板按图1放置,O是边BC(DF)的中点,BC=12cm.如图2,将△ABC绕点O顺时针旋转60°,AC与EF相交于点G,则FG的长是cm.
 13. 如图,将线段AB绕点A顺时针旋转30°,得到线段AC.若AB=12,则点B经过的路径 长度为 .(结果保留π)
13. 如图,将线段AB绕点A顺时针旋转30°,得到线段AC.若AB=12,则点B经过的路径 长度为 .(结果保留π)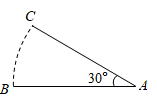 14. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .
14. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .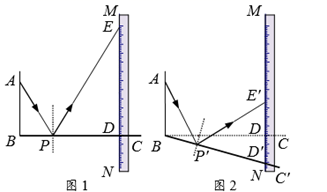 (1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.15. 一副三角板按图放置,是边的中点, . 如图 , 将绕点逆时针旋转,使得点落在线段上不与点重合 , 则的长是 .
(1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.15. 一副三角板按图放置,是边的中点, . 如图 , 将绕点逆时针旋转,使得点落在线段上不与点重合 , 则的长是 . 16. 图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等。当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动。当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3)。
16. 图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=140cm,AB=BC=CQ=QA=60cm,OQ=50cm,O,P两点间距与OQ长度相等。当OQ绕点O转动时,点A,B,C的位置随之改变,点B恰好在线段MN上来回运动。当点B运动至点M或N时,点A,C重合,点P,Q,A,B在同一直线上(如图3)。 (1)、点P到MN的距离为cm。(2)、当点P,O,A在同一直线上时,点Q到MN的距离为cm。17. 如图1是一款便携式拉杆车,其侧面示意图如图2所示,前轮的直径为 , 拖盘与后轮相切于点N,手柄 . 侧面为矩形ABCD的货物置于拖盘上, , . 如图3所示,倾斜一定角度拉车时,货物绕点B旋转,点C落在上,若 , 则的长为 , 同一时刻,点C离地面高度 , 则点A离地面高度为 .
(1)、点P到MN的距离为cm。(2)、当点P,O,A在同一直线上时,点Q到MN的距离为cm。17. 如图1是一款便携式拉杆车,其侧面示意图如图2所示,前轮的直径为 , 拖盘与后轮相切于点N,手柄 . 侧面为矩形ABCD的货物置于拖盘上, , . 如图3所示,倾斜一定角度拉车时,货物绕点B旋转,点C落在上,若 , 则的长为 , 同一时刻,点C离地面高度 , 则点A离地面高度为 .

三、作图题(共6分)
-
18. 如图,在的方格纸中,的顶点均在格点上,请按要求画图.
 (1)、在图中作一个以点A,B,C,D为顶点的格点四边形,且该四边形为中心对称图形.(2)、在图中找一个格点E,连结 , 使将的面积分为.
(1)、在图中作一个以点A,B,C,D为顶点的格点四边形,且该四边形为中心对称图形.(2)、在图中找一个格点E,连结 , 使将的面积分为.四、解答题(共4题,共27分)
-
19. 在四边形ABCD中,对角线AC、BD交于点O,若四边形ABCD是正方形,如图1:则有AC=BD,AC⊥BD.

旋转图1中的Rt△COD到图2所示的位置,AC’与BD’有什么关系?(直接写出);
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC’与BD’又有什么关系?写出结论并证明.
20. 如图1是某小车侧面示意图,图2是该车后备箱开启侧面示意图,具体数据如图所示(单位:cm)且AF∥BE,sin∠BAF= , 箱盖开启过程中,点B,E绕点A沿逆时针方向转动相同角度,分别到点B',E'的位置,点E'在线段EB的延长线上.若直线BE⊥B'E'. (1)、求旋转角∠EAE'的度数.(2)、若BE'=28,求AB的长度.21. 如图1,矩形DEFG中,DG=2,DE=3,Rt△ABC中,∠ACB=90°,CA=CB=2,FG,BC的延长线相交于点O,且FG⊥BC,OG=2,OC=4。将△ABC绕点O逆时针旋转α(0°≤α<180°)得到△A'B'C'。
(1)、求旋转角∠EAE'的度数.(2)、若BE'=28,求AB的长度.21. 如图1,矩形DEFG中,DG=2,DE=3,Rt△ABC中,∠ACB=90°,CA=CB=2,FG,BC的延长线相交于点O,且FG⊥BC,OG=2,OC=4。将△ABC绕点O逆时针旋转α(0°≤α<180°)得到△A'B'C'。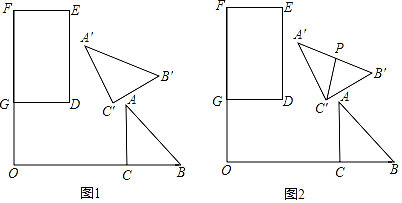 (1)、当α=30°时,求点C'到直线OF的距离。(2)、在图1中,取A'B'的中点P,连结C'P,如图2。
(1)、当α=30°时,求点C'到直线OF的距离。(2)、在图1中,取A'B'的中点P,连结C'P,如图2。①当C'P与矩形DEFG的一条边平行时,求点C'到直线DE的距离。
②当线段A'P与矩形DEFG的边有且只有一个交点时,求该交点到直线DG的距离的取值范围。
22. 如图1,在平面直角坐标系中,点O为坐标原点,点A的坐标为 , 直线经过点、.将四边形绕点O按顺时针方向旋转α度得到四边形 , 此时直线、直线分别与直线相交于点P、Q. (1)、四边形的形状是 , 当时,的值是;(2)、①如图2,当四边形的顶点落在y轴正半轴上时,求的值;
(1)、四边形的形状是 , 当时,的值是;(2)、①如图2,当四边形的顶点落在y轴正半轴上时,求的值;②如图3,当四边形的顶点落在直线上时,求的面积;
(3)、在四边形旋转过程中,当时,是否存在这样的点P和点Q,使得 , 若存在,请直接写出点P的坐标;若不存在,请说明理由.五、实践探究题(共4题,共36分)
-
23. 在一次数学研究性学习中, 小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1) ,其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动。
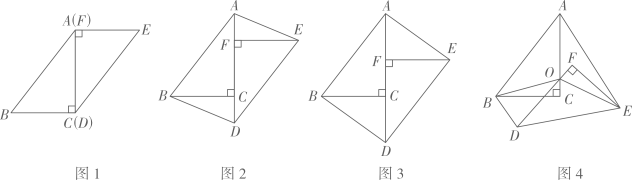 (1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。
(1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移。【思考】图2中的四边形ABDE是平行四边形吗?请说明理由。
【发现】当纸片DEF平移到某一位置时,小兵发现四边形AB DE为矩形(如图3)。求AF的长。
(2)、活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4)。【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由。
24. 如图 (1)、【原题初探】
(1)、【原题初探】小明在数学作业本中看到有这样一道作业题:如图1,P是正方形ABCD内一点,连结PA,PB,PC.现将△PAB绕点B顺时针旋转90°得到的△P'CB,连接PP'.若PA= ,PB=3,∠APB=135°,求PC的长和正方形ABCD的边长.
(2)、【变式猜想】如图2,若点Р是等边△ABC内的一点,且PA=3,PB=4,PC=5,请猜想∠APB的度数,并说明理由.
(3)、【拓展应用】
聪明的小明经过上述两小题的训练后,善于反思的他又提出了如下的问题:如图3,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,请求出BD的长度.25. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD. (1)、[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.(2)、[探究2]如图2,连结AC′,过点D′作 交BD于点M,线段D′M与DM相等吗?请说明理由.(3)、[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.26. 图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.
(1)、[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.(2)、[探究2]如图2,连结AC′,过点D′作 交BD于点M,线段D′M与DM相等吗?请说明理由.(3)、[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.26. 图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.
探索发现:
(1)、如图①,BC与BD的数量关系是;(2)、如图①,CD与AB的数量关系是 ▲ ;并说明理由.(3)、如图②,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想BF,BP,BD三者之间的数量关系,并证明你的结论;(4)、若点P是线段CB延长线上一动点,按照(3)中的作法,请在图③中补全图象,并直接写出BF、BP、BD三者之间的数量关系.
-