备考2024年浙江中考数学一轮复习专题24.1图形的轴对称 基础夯实
试卷更新日期：2024-03-02 类型：一轮复习
一、选择题（每题3分，共30分）
-
1. 第19届亚运会于2023年9月在杭州举行，下列历届亚运会会徽是轴对称图形的是（ ）A、
B、
C、
D、
2. 如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是（ ）
A、① B、② C、⑤ D、⑥3. 如图，是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击出，该球最后落入1号袋，经过反射的次数是（ ）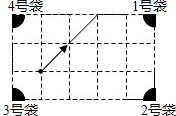
A、4次 B、5次 C、6次 D、7次4. 从正三角形、正方形、正五边形、正六边形中任选一个，选中的恰好既是轴对称图形，又是中心对称图形的概率是（ ）A、 B、 C、 D、5. 如图，中，D点在上，将D点分别以为对称轴，画出对称点E、F，并连接 ， 根据图中标示的角度，的度数为（ ）
A、 B、 C、 D、6. 如图，在四边形刚好是中点，P、Q分别是线段上的动点，则的最小值为（ ）
A、12 B、15 C、16 D、187. 如图，已知正六边形ABCDEF中，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的值最小时，BP与HG的夹角（锐角）度数为 （ ）度．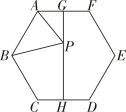
A、 B、60 C、 D、8. 用矩形纸片折出直角的平分线，下列折法正确的是（ ）A、
B、
C、
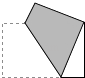D、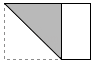
9. 如图，将一张正方形纸片经两次对折，并剪出一个菱形小洞后展开铺平，得到的图形是图中的哪一个（ ）
A、
B、
C、
D、
10. 学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的(如图所示)．
从图中可知，小敏画平行线的依据是（ ）
①两直线平行，同位角相等；②两直线平行，内错角相等；③同位角相等，两直线平行；④内错角相等，两直线平行．
A、①或② B、②或③ C、③或④ D、①或④二、填空题（每题4分，共24分）
-
11. 在“线段、角、直角三角形、等边三角形”这四个图形中，对称轴最多的图形是 .12. 如图，在正方形网格中，黑色部分的图形构成一个轴对称图形，现任意选取一个白色的小方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是 ．
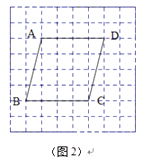
13. 如图，在平面直角坐标系中，平行四边形的坐标分别为、、、 ， 点是边上的一个动点，若点关于的对称点为 ， 则的最小值为 ．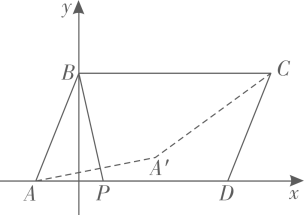
14. 如图，△ABC为等腰直角三角形，∠ABC=90°，点P在AC的延长线上，且AC=CP=4，将△ABC沿AB方向平移得到△A'B'C'，连结PA'，PC'，则△PA'C'的周长的最小值为.
15. 将一张正方形纸片ABCD按如图所示的方式折叠，AE、AF为折痕，点B、D折叠后的对应点分别为、 ， 若 ， 则∠EAF的度数为
16. 由沈康身教授所著，数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事：如图，三姐妹为了平分一块边长为1的祖传正方形地毯，先将地毯分割成七块，再拼成三个小正方形（阴影部分）．则图中AB的长应是 ．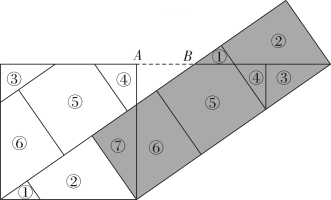
三、作图题（共4题，共30分）
-
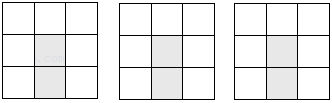
17. 在3×3的方格图中，有三个小正方形格子被涂成阴影，请在剩下的7个白色格子中选择2个格子，将它涂上阴影，使得整个图形是一个轴对称图形，要求画出三种不同形状的图形.
18. 在平面直角坐标系中，△ABC的三个顶点分别是A（2，4），B（1，1），C（3，2）．
(1)、画出△ABC关于x轴对称的△A1B1C1 ， 并写出点A1的坐标：A1（ ▲ ）；(2)、求△ABC的面积；(3)、在y轴上找一点P（保留作图痕迹），使PA+PB的值最小，请直接写出点P的坐标：P（ ， ）．19. 在棋盘中建立如图的直角坐标系，三颗棋子A ， O ， B的位置如图1，它们分别是（-1，1），（0，0）和（1，0）．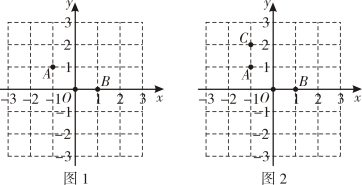
(1)、如图2，添加棋子C ， 使A ， O ， B ， C四颗棋子组成一个轴对称图形，请在图中画出该图形的对称轴；(2)、要在其他格点位置添加一颗棋子P ， 使A ， O ， B ， P四颗棋子组成一个轴对称图形，请直接写出棋子P的所有可能位置的坐标．20. 综合题。(1)、如图，在图1所给方格纸中，每个小正方形边长都是1，标号为①②③的三个三角形均为格点三角形（顶点在方格顶点处），请按要求将图2中的指定图形分割成三个三角形，使它们与标号为①②③的三个三角形分别对应全等．（分割线画成实线．）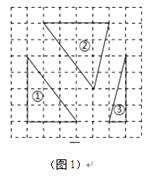
(2)、如图3，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
①在图中画出与△ABC关于直线L成轴对称的 ；
②请直线L上找到一点P，使得PC + PB的距离之和最小．
四、解答题（共3题，共27分）
-
21. 如图， 纸上有五个边长为1的小正方形组成的图形纸（图1），我们可以把它剪开拼成一个正方形（图2）.
(1)、图中拼成的正方形的面积是； 边长是；(2)、你能把十个小正方形组成的图形纸 （图3），剪开并拼成正方形吗？ 若能， 请仿照图 的形式把它重新拼成一个正方形. 并求出这个正方形的边长是 .22. 如图，矩形纸片ABCD置于坐标系中，ABx轴，BCy轴，AB＝4，BC＝3，点A（-3，4），翻折矩形纸片使点D落在对角线AC上的H处，AG是折痕.
(1)、求DG的长；(2)、在x轴上是否存在点N，使BN+DN的值最小，若存在，求出这个最小值及点N的坐标；若不存在.请说明理由；(3)、点P从点A出发，沿折线A-B-C运动，到达点C时停止运动，是否存在一点P，使△PBM是等腰三角形，若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由.23. 问题情境：数学活动课上，同学们开展了以“矩形纸片折叠”为主题的探究活动（每个小组的矩形纸片规格相同），已知矩形纸片宽 ．
(1)、动手实践：如图1，A小组将矩形纸片折叠，点D落在边上的点E处，折痕为 ， 连接 ， 然后将纸片展平，得到四边形 ． 试判断四边形的形状，并加以证明．(2)、如图2，B小组将矩形纸片对折使与重合，展平后得到折痕 ， 再次过点A折叠使点D落在折痕上的点N处，得到折痕 ， 连结 ， 展平后得到四边形 ， 请求出四边形的面积．(3)、深度探究：
如图 3，C小组将图1中的四边形剪去，然后在边上取点G，H，将四边形沿折叠，使A点的对应点始终落在边上（点不与点D，F重合），点E落在点处，与交于点T．探究①当在上运动时，的周长是否会变化？如变化，请说明理由；如不变，请求出该定值．
探究②直接写出四边形面积的最小值．
五、实践探究题（共9分）
-
24. 请同学们利用以下图形解决问题：
(1)、如图1，一个边长为5cm的正方形被分割成四个完全相同的直角三角形，现将这四个直角三角形分别沿着正方形四条边向外翻折，翻折后得到图2所示的大正方形，求该大正方形的边长.(2)、如图3，一个边长为5cm的正方形被分割成四个完全相同的直角三角形和一个阴影小正方形（无缝隙、不重叠），现将这四个直角三角形分别沿着正方形四条边向外翻折，翻折后得到图4所示的大正方形.①若阴影小正方形的边长为2，求图4中大正方形的边长.
②若图4中大正方形的边长为正整数，则阴影小正方形的边长是 ▲ cm .