备考2024年浙江中考数学一轮复习专题24.2图形的轴对称 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 美术老师写的下列四个字中,为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,将七巧板的其中几块拼成一个多 边形,所拼多边形为轴对称图形的是( )
2. 如图,将七巧板的其中几块拼成一个多 边形,所拼多边形为轴对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、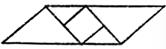 3. 如图,两盘灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A',B'的位置描述正确是( )
3. 如图,两盘灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A',B'的位置描述正确是( ) A、关于轴对称 B、关于轴对称 C、关于原点对称 D、关于直线对称4. 若点 与点 关于 轴对称,则A、2 B、0 C、-2 D、-45. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、关于轴对称 B、关于轴对称 C、关于原点对称 D、关于直线对称4. 若点 与点 关于 轴对称,则A、2 B、0 C、-2 D、-45. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )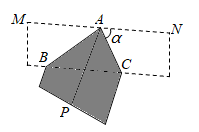 A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm26. 直角坐标系中已知两点以及动点 , 当四边形的周长最小时,求比值.( )A、 B、-2 C、 D、-37. 矩形纸片中, , 将纸片对折,使顶点A与顶点C重合,得折痕 , 将纸片展开铺平后再进行折叠,使顶点B与顶点D重合,得折痕 , 展开铺平后如图所示.若折痕与较小的夹角记为 , 则( )
A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm26. 直角坐标系中已知两点以及动点 , 当四边形的周长最小时,求比值.( )A、 B、-2 C、 D、-37. 矩形纸片中, , 将纸片对折,使顶点A与顶点C重合,得折痕 , 将纸片展开铺平后再进行折叠,使顶点B与顶点D重合,得折痕 , 展开铺平后如图所示.若折痕与较小的夹角记为 , 则( ) A、 B、 C、 D、8. 如图,边长为1的正方形ABCD沿着过中心O的直线EF (EF不为对角线)对折,下列结论不正确的是( )
A、 B、 C、 D、8. 如图,边长为1的正方形ABCD沿着过中心O的直线EF (EF不为对角线)对折,下列结论不正确的是( ) A、△DHF的周长为定值 B、∠HOF的度数为定值 C、四边形HCNO的面积为定值 D、△NOE的面积为定值9. 如图1,在矩形ABCD中,点E,F,G分别是边AD,BC,AB的中点,连结EF, , 点H是EF上一动点,设FH的长为x,GH与BH长度的和为y.图2是y关于x的函数图象,点P为图象上的最低点,则函数图象的右端点Q的坐标为( )
A、△DHF的周长为定值 B、∠HOF的度数为定值 C、四边形HCNO的面积为定值 D、△NOE的面积为定值9. 如图1,在矩形ABCD中,点E,F,G分别是边AD,BC,AB的中点,连结EF, , 点H是EF上一动点,设FH的长为x,GH与BH长度的和为y.图2是y关于x的函数图象,点P为图象上的最低点,则函数图象的右端点Q的坐标为( )
 A、 B、 C、 D、10. 将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM,GN是折痕,若正方形EFGH与五边形MCNGF的面积相等,则 的值是( )
A、 B、 C、 D、10. 将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM,GN是折痕,若正方形EFGH与五边形MCNGF的面积相等,则 的值是( )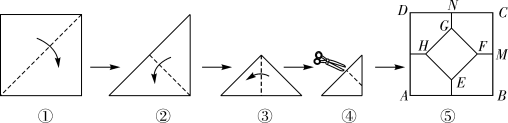 A、 B、 -1 C、 D、
A、 B、 -1 C、 D、二、填空题(每题4分,共28分)
-
11. 若点P(4,3)关于y轴的对称点是点P'(a+1,b-2),则a= , b= .12. 在平面直角坐标系中,点A在第三象限,点B在第四象限,且点A、B关于y轴对称.若点B的坐标为 , 则点A的坐标为.(用字母表示)13. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
 14. 如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=3,点E是线段BC上的一个动点(点E不与点B,C重合),连接GB,GE,将△GBE关于直线GE对称的三角形记作△GFE,当点E运动到使点F落在矩形任意一边所在的直线上时,则线段BE的长是 .
14. 如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=3,点E是线段BC上的一个动点(点E不与点B,C重合),连接GB,GE,将△GBE关于直线GE对称的三角形记作△GFE,当点E运动到使点F落在矩形任意一边所在的直线上时,则线段BE的长是 .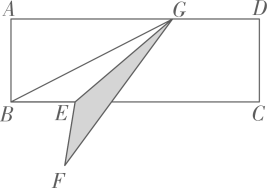 15. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F. 已知∠AOB=120°,OA=6,则 的度数为 , 折痕CD的长为 .
15. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F. 已知∠AOB=120°,OA=6,则 的度数为 , 折痕CD的长为 .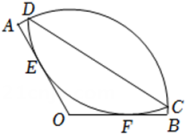 16. 如图1,点E,F是矩形纸片ABCD的边AD上两点,将△ABE和△DCF分别沿BE和CF翻折后(如图2),四边形EDAF恰为矩形,其中 , 如果梯形EBCF的面积比矩形ABCD的面积小300cm2 , 则折纸后三层重叠部分即四边形MN的面积为cm2.
16. 如图1,点E,F是矩形纸片ABCD的边AD上两点,将△ABE和△DCF分别沿BE和CF翻折后(如图2),四边形EDAF恰为矩形,其中 , 如果梯形EBCF的面积比矩形ABCD的面积小300cm2 , 则折纸后三层重叠部分即四边形MN的面积为cm2.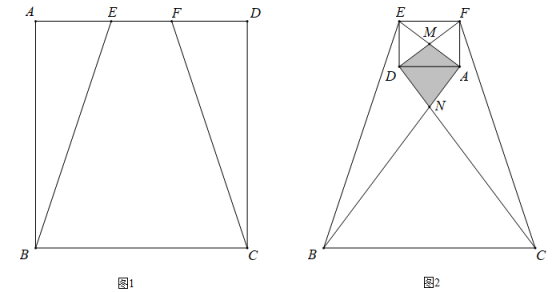 17. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.
17. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.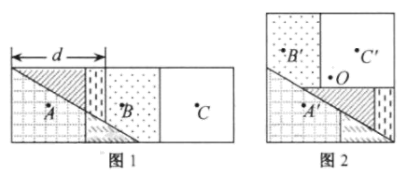
三、作图题(共9分)
-
18. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
 (1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.
(1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
四、解答题(共4题,共33分)
-
19. 临海大桥主塔是一个轴对称图形(如图所示),小明测得桥面宽度 米, ,求点 到桥面 的距离.(结果精确到0.1米,参考数据: )
 20. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,
20. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF, (1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.21. 如图,AD是锐角△ABC中BC边上的高,将△ABD沿AB所在的直线翻折得到△ABE,将△ADC沿AC所在的直线翻折得到△AFC,延长EB,FC相交于点P.
(1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.21. 如图,AD是锐角△ABC中BC边上的高,将△ABD沿AB所在的直线翻折得到△ABE,将△ADC沿AC所在的直线翻折得到△AFC,延长EB,FC相交于点P. (1)、如图1,若∠BAC=45°,求证:四边形AEPF为正方形;(2)、如图2,若∠BAC=55°,当△PBC是等腰三角形时,求∠BAD的度数;(3)、如图3,连结EF,分别交AB,AC于点G、H,连结BH交AD于点M,若∠BAC=60°,
(1)、如图1,若∠BAC=45°,求证:四边形AEPF为正方形;(2)、如图2,若∠BAC=55°,当△PBC是等腰三角形时,求∠BAD的度数;(3)、如图3,连结EF,分别交AB,AC于点G、H,连结BH交AD于点M,若∠BAC=60°,①求∠PEF=▲ 度;
②若AB=10,CH=1,求△ABM的面积.
22. 根据以下素材,探索完成任务.如何给桥护栏挂小彩灯
素材1
图1是桥的护栏实物图,护栏长200米,高1.6米,图2是桥护栏示意图,为了使彩灯挂起来整齐美观,设计小组首先制作了外缘呈抛物线型模板,然后用该模板在图纸上绘制抛物线图案,彩灯沿抛物线摆放

素材2
方案一:护栏中间正好可以摆5具模板,绘制5条抛物线图案连成一条波浪线,每条抛物线的顶点落在护栏的上下边
方案二:将模板一部分放入护栏,绘制若干条抛物线图案,靠上下两边连成两条波浪线,每条抛物线的高度都相等,相对两条抛物线的顶点之间的距离h为0.7米.
方案三:将方案一和方案二中的抛物线图案各若干条,沿护栏下边摆放,大的图案摆在中间,小的图案摆两边,连成一条波浪线,且整个小彩灯图案呈轴对称图形,每条抛物线图案保持完整,两边能摆尽摆,可以有空余

任务
问题解决
一
确定抛物线形状
求出模板抛物线的函数解析式
二
确定方案二中一条抛物线图案的宽度和摆放方案
求出其中一条抛物线图案的宽度.每边这样的图案最多可以摆放几个?
三
设计方案三摆放方案
确定大小抛物线图案各需多少个,并给出摆放方案
-