备考2024年浙江中考数学一轮复习专题23.1命题与证明基础夯实

试卷更新日期：2024-03-02 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列语句中，是定义的是（）

A、两点确定一条直线 B、在同一平面内，不相交的两条直线叫做平行线 C、三角形的角平分线是一条线段 D、同角的余角相等

查看试题解析
2. 下列语句中是命题的有（）个．
①三角形的内角和等于180°； ②如果|x|＝5，那么x＝5； ③1月份有30天； ④作一条线段等于已知线段； ⑤一个锐角与一个钝角互补吗？

A、2 B、3 C、4 D、5

查看试题解析
3. 下列定理中没有逆定理的是（）

A、两直线平行，内错角相等 B、角平分线上的点到这个角两边的距离相等 C、对顶角相等 D、在同一个三角形中，等边对等角

查看试题解析
4. 对于命题“如果∠1＝∠2＝90°，那么∠1与∠2互补”，能说明这个命题的逆命题是假命题的反例是（）

A、∠1＝80°，∠2＝110° B、∠1＝10°，∠2＝169° C、∠1＝60°，∠2＝120° D、∠1＝60°，∠2＝140°

查看试题解析
5. 下面说法中正确的是（）

A、“同位角相等”的题设是“两个角相等” B、“相等的角是对顶角”是假命题 C、如果ab=0，那么a+b=0是真命题 D、“任何偶数都是4的倍数”是真命题

查看试题解析
6. 下列命题的逆命题是真命题的是（　　）

A、全等三角形的对应角相等 B、若a＞0，b＞0，则a+b＞0 C、直角三角形斜边上的中线等于斜边的一半 D、相反数的绝对值相等

查看试题解析
7. 下列命题中：①任意三点确定一个圆；②同弧或等弧所对的圆心角相等；③平分弦的直径垂直于弦；④半圆所对的弦是直径.真命题的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
8. 下列说法正确的是（）

A、每个定理都有逆定理 B、每个命题都有逆命题 C、假命题没有逆命题 D、真命题的逆命题是真命题

查看试题解析
9. 已知命题“若 $a^{2} > b^{2}$ ，则 $a > b$ ”，下列说法正确的是（　　）

A、它是一个真命题 B、它是一个假命题，反例 $a = - 3 ， b = - 2$ C、它是一个假命题，反例 $a = 3 ， b = - 2$ D、它是一个假命题，反制 $a = 3 ， b = 2$

查看试题解析
10. 定理“等腰三角形的两个底角相等”的逆定理是（）

A、有两个角不相等的三角形不是等腰三角形 B、不是等腰三角形的两个角不相等 C、有两个底角相等的三角形是等腰三角形 D、有两个角相等的三角形是等腰三角形

查看试题解析
11. 布鲁斯先生、他的妹妹、他的儿子，还有他的女儿都是网球选手．这四人中有以下情况：①最佳选手的孪生同胞与最差选手性别不同：②最佳选手与最差选手年龄相同．则这四人中最佳选手是（）

A、布鲁斯先生的女儿 B、布鲁斯先生的妹妹 C、布鲁斯先生的儿子 D、布鲁斯先生

查看试题解析
12. 某社区运动会共设置了 $A ， B ， C ， D ， E$ 五个比赛项目，甲、乙、丙、丁、戊五人一起去报名参加比赛，每人至少报名参加一个比赛项目.已知甲、乙、丙、丁分别报名参加了其中2，3，3，4个比赛项目，而 $A ， B ， C ， D$ 四个比赛项目在这五人中分别有1，2，2，3人报名，则这五人中报名参加比赛项目 $E$ 的人数有（）

A、2人 B、3人 C、4人 D、5人

查看试题解析
13. 如图，在探究“幻方”、“幻圆”的活动课上，学生们感悟到我国传统数学文化的魅力.一个小组尝试将数字 $- 5 ， - 4 ， - 3 ， - 2 ， - 1 ， 0 ， 1 ， 2 ， 3 ， 4 ， 5 ， 6$ 这12 个数填入“六角幻星”图中，使6条边上四个数之和都相等.部分数字已填入圆圈中，则a的值为（）

A、 $- 4$ B、 $- 3$ C、3 D、4

查看试题解析

二、填空题（每题3分，共21分）

14. 把命题“线段垂直平分线上的点到这条线段的两个端点的距离相等”改写成“如果…，那么…．”的形式．

查看试题解析
15. “直角三角形两个锐角互余”的逆命题是，该逆命题是一个命题（填“真”或“假”）.

查看试题解析
16. 反证法是数学中经常运用的一类“间接证明法”.用反证法证明：“已知在△ABC中，AB=AC，求证：∠B＜90°”时，第一步应假设.

查看试题解析
17. 已知命题“在△ABC中，若AC²+BC²≠AB² ，则∠C≠90°”，用反证法，其步骤为：假设，根据，一定有，但这与已知相矛盾，因此假设是错误的，故原命题是真命题。

查看试题解析
18. 关于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，有以下命题：若 $① a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + b x + c = 0$ 两根为 $- 1$ 和 $2$ ，则 $2 a + c = 0$ ；③若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；④若 $a x^{2} + b x + c = 0$ 有两个相等的实数根，则 $a x^{2} + b x + c = 1$ 无实数根．其中真命题是.

查看试题解析
19. 甲和乙玩一个猜数游戏，规则如下：已知五张纸牌上分别写有1、2、3、4、5五个数字，现甲、乙两人分别从中各自随机抽取一张，然后根据自己手中的数推测谁手上的数更大.甲看了看自己手中的数，想了想说：我不知道谁手中的数更大；乙听了甲的判断后，思索了一下说：我也不知道谁手中的数更大.假设甲、乙所作出的推理都是正确的，那么乙手中的数是.

查看试题解析
20. 电脑系统中有个“扫雷”游戏，要求游戏者标出所有的雷，游戏规则：一个方块下面最多埋一个雷，如果无雷，掀开方块下面就标有数字，提醒游戏者此数字周围的方块（最多八个）中雷的个数（实际游戏中，0通常省略不标，为方便大家识别与印刷，我把图乙中的0都标出来了，以示与未掀开者的区别），如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷．图乙是张三玩游戏中的局部，图中有4个方块已确定是雷（方块上标有旗子），则图乙第一行从左数起的七个方块中（方块上标有字母），能够确定一定是雷的有．（请填入方块上的字母）

查看试题解析

三、解答题（共7题，共60分）

21. 证明命题“等腰三角形两腰上的中线相等”。(自己画出图形)
已知：

求证：

证明：

查看试题解析
22. 用反证法证明下列问题。
如图，在△ABC中，点D，E分别在AC，AB上，BD，CE相交于点O。

求证：BD和CE不可能互相平分。

查看试题解析
23.

(1)、写出命题“等腰三角形底边上的高线与中线互相重合”的逆命题，并判断真假；

(2)、若该命题的逆命题为真命题，请证明；若该命题的逆命题为假命题，请举出反例.

查看试题解析
24. 定义：两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”．如图1，在△ABC中，若AB²+AC²-AB⋅AC=BC² ，则△ABC是“和谐三角形”．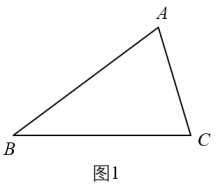

(1)、等边三角形一定是“和谐三角形”，是命题（填“真”或“假”）．

(2)、若Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b>a，若△ABC 是“和谐三角形”，求a：b：c．

查看试题解析
25. 定义：在一个三角形中，若存在两条边x和y，使得y＝x² ，则称此三角形为“平方三角形”，x称为平方边．

(1)、“若等边三角形为平方三角形，则面积为 $\frac{\sqrt{3}}{4}$ ”是命题；
“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是命题；（填“真”或“假”）

(2)、如图，在△ABC中，D是BC上一点，若∠CAD＝∠B，CD＝1，求证：△ABC为平方三角形；

(3)、若a，b，c是平方三角形的三条边，平方边a＝2，若三角形中存在一个角为60°，求c的值．

查看试题解析
26. 如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“优三角形”，这两条边的比称为“优比”（若这两边不等，则优比为较大边与较小边的比），记为 $k$ .

(1)、命题：“等边三角形为优三角形，其优比为1”，是真命题还是假命题？

(2)、已知 $△ A B C$ 为优三角形， $A B = c$ ， $A C = b$ ， $B C = a$ ，
①如图1，若 $∠ A C B = 90 °$ ， $b \geq a$ ， $b = 6$ ，求 $a$ 的值.

②如图2，若 $c \geq b \geq a$ ，求优比 $k$ 的取值范围.

(3)、已知 $△ A B C$ 是优三角形，且 $∠ A B C = 120 °$ ， $B C = 4$ ，求 $△ A B C$ 的面积.

查看试题解析
27. 定义：如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“奇异三角形”，这条中线为“奇异中线”。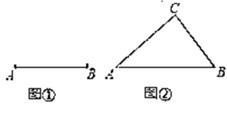

(1)、请根据定义解答：
①判断，命题：“如果直角三角形是奇异三角形，那么奇异中线一定是较长直角边上的中线”是真命题还是假命题；

②请用直尺和圆规在图①中画一个以AB为边的“奇异三角形“；

(2)、如图②，在Rt△ABC中，∠C=90°， $\frac{B C}{A C} = \frac{\sqrt{3}}{2}$ ，求证：△ABC是“奇异三角形”．

(3)、已知，等腰△ABC是“奇异三角形”，AB=AC=20，求底边BC的长。(结果保留根号)

查看试题解析

备考2024年浙江中考数学一轮复习专题23.1命题与证明 基础夯实

一、选择题（每题3分，共30分）

二、填空题（每题3分，共21分）

三、解答题（共7题，共60分）

备考2024年浙江中考数学一轮复习专题23.1命题与证明基础夯实