备考2024年浙江中考数学一轮复习专题22.1圆 基础夯实
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 下列命题正确的是( )A、三个点确定一个圆 B、圆是轴对称图形,其对称轴是直径 C、90°的圆周角所对的弦是直径 D、平分弦的直径垂直于弦2. 下列语句中不正确的有( )
①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤圆内接四边形的对角互补.
A、5个 B、4个 C、3个 D、2个3. 如图,是的直径,点C、D、E在上,若 , , 且 , 则为( )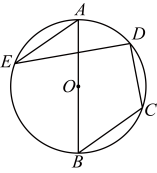 A、 B、6 C、 D、4. 如图,点 、 、 在 上,若 ,则 的度数是( )
A、 B、6 C、 D、4. 如图,点 、 、 在 上,若 ,则 的度数是( )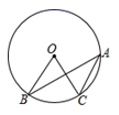 A、18° B、36° C、54° D、72°5. 如果一个三角形的外心在三角形的外部,那么这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定6. 如图,在的内接四边形中,点在的延长线上.若 , 则的度数是( )
A、18° B、36° C、54° D、72°5. 如果一个三角形的外心在三角形的外部,那么这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定6. 如图,在的内接四边形中,点在的延长线上.若 , 则的度数是( )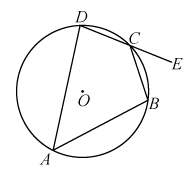 A、 B、 C、 D、7. 如图,E为Rt△ABC的直角边BC上一点,以CE为半径的半圆与斜边AB相切于点D.已知AD=6,BD=4,则⊙E的半径的长为( )
A、 B、 C、 D、7. 如图,E为Rt△ABC的直角边BC上一点,以CE为半径的半圆与斜边AB相切于点D.已知AD=6,BD=4,则⊙E的半径的长为( ) A、3.5 B、3 C、2.5 D、28. 如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A、3.5 B、3 C、2.5 D、28. 如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( ) A、7.5cm B、10cm C、12.5cm D、15cm9. 如图,点O在线段AB上,OA=2,OB=6,以O为圆心,OA为半径作⊙O,点M在⊙O上运动,连结MB,以MB为一边作等边△MBC,连结AC,则AC长度的最小值为( )
A、7.5cm B、10cm C、12.5cm D、15cm9. 如图,点O在线段AB上,OA=2,OB=6,以O为圆心,OA为半径作⊙O,点M在⊙O上运动,连结MB,以MB为一边作等边△MBC,连结AC,则AC长度的最小值为( )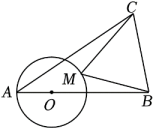 A、22 B、22 C、42 D、4210. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为( )
A、22 B、22 C、42 D、4210. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为( ) A、1米 B、2米 C、3米 D、4米
A、1米 B、2米 C、3米 D、4米二、填空题(每题3分,共18分)
-
11. 平面上一点到⊙O上的点的最长距离为9cm,最短距离为3cm,则⊙O的半径是 .12. 已知△ABC的边BC= , 且△ABC内接于半径为4cm的⊙O , 则∠A的度数为 .13. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,则弦AB的长度为 ;当点E在⊙G的运动过程中,线段FG的长度的最小值为 .
 14. 如图,线段是的直径,弦于点H,点是弧上任意一点(不与B,C重合), , .延长线段交的延长线于点E,直线交于点N,连结交于点F,则 , .
14. 如图,线段是的直径,弦于点H,点是弧上任意一点(不与B,C重合), , .延长线段交的延长线于点E,直线交于点N,连结交于点F,则 , . 15. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 .
15. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 . 16. 如图,在Rt中, , 分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当时,阴影部分的面积为.
16. 如图,在Rt中, , 分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当时,阴影部分的面积为.
三、作图题(共6分)
-
17. 如图,在6×6的正方形网格中,网格线的交点称为格点,点A , B , C都是格点.已知每个小正方形的边长为1.
 (1)、画出△ABC的外接圆⊙O , 并直接写出⊙O的半径;(2)、在圆上找一个点P , 使得△PAC是直角三角形,且点P在格点上.
(1)、画出△ABC的外接圆⊙O , 并直接写出⊙O的半径;(2)、在圆上找一个点P , 使得△PAC是直角三角形,且点P在格点上.四、解答题(共6题,共46分)
-
18. 如图,直线与相切于点C , 射线与交于点D , E , 连结 . 连结 .
 (1)、求证:;(2)、若 , , 求弧的长.19. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交BC于点D,过点D作DE∥BC交AC的延长线于点E.
(1)、求证:;(2)、若 , , 求弧的长.19. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交BC于点D,过点D作DE∥BC交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、若DE=2,CE=1,求BD的长度.20. 如图,内接于 , , 它的外角的平分线交于点D , 连接交于点F .
(1)、求证:DE是⊙O的切线;(2)、若DE=2,CE=1,求BD的长度.20. 如图,内接于 , , 它的外角的平分线交于点D , 连接交于点F . (1)、若 , 求的度数.(2)、求证: .(3)、若 , 当 , 求的度数(用含的代数式表示).21. 如图,是的直径,弦与点 , 已知 , 点为上任意一点,(点不与重合),连结并延长与交于点 , 连 .
(1)、若 , 求的度数.(2)、求证: .(3)、若 , 当 , 求的度数(用含的代数式表示).21. 如图,是的直径,弦与点 , 已知 , 点为上任意一点,(点不与重合),连结并延长与交于点 , 连 .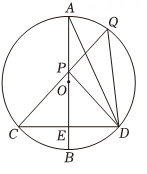 (1)、求的长.(2)、若 , 直接写出的长.(3)、①若点在之间(点不与点重合),求证: .
(1)、求的长.(2)、若 , 直接写出的长.(3)、①若点在之间(点不与点重合),求证: .②若点在之间(点不与点重合),求与满足的关系.
22. 内接于 , 点I是的内心,连接并延长交于点D,连接 , 已知 ,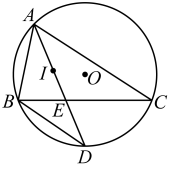 (1)、连接 , , 则(用含有的代数式表示)(2)、求证:;(3)、连接 , 若 , 求的最小值(4)、若 , 为等腰三角形,直接写出的值.23. 如图,四边形ABCD是⊙O 的内接四边形,对角线AC,BD交于点E,AB=AC.
(1)、连接 , , 则(用含有的代数式表示)(2)、求证:;(3)、连接 , 若 , 求的最小值(4)、若 , 为等腰三角形,直接写出的值.23. 如图,四边形ABCD是⊙O 的内接四边形,对角线AC,BD交于点E,AB=AC. (1)、如图1,若BD是⊙O的直径,求证:∠BAC=2∠ACD;(2)、如图2,若BD⊥AC,DE =3,CE=4,求BE的长;(3)、如图3,若∠ABC+∠DCB=90°,AD=7,BC=24,求AB的长;(4)、在(3)的条件下,保持BC不动,使AD在⊙O上滑动,(滑动中AD长度保持不变)直接写出BD+AC的最大值.
(1)、如图1,若BD是⊙O的直径,求证:∠BAC=2∠ACD;(2)、如图2,若BD⊥AC,DE =3,CE=4,求BE的长;(3)、如图3,若∠ABC+∠DCB=90°,AD=7,BC=24,求AB的长;(4)、在(3)的条件下,保持BC不动,使AD在⊙O上滑动,(滑动中AD长度保持不变)直接写出BD+AC的最大值.五、实践探究题(共2题,共20分)
-
24. 根据背景素材,探索解决问题.
测算石拱桥拱圈的半径
素材1
某数学兴趣小组测算一座石拱桥拱圈的半径(如图1),石拱桥由矩形的花岗岩叠砌而成,上、下的花岗岩错缝连接(花岗岩的各个顶点落在上、下花岗岩各边的中点,如图2所示).

素材2
通过观察发现A,B,C三个点都在拱圈上,A是拱圈的最高点,且在两块花岗岩的连接处,B,C两个点都是花岗岩的顶点(如图3).

素材3
如果没有带测量工具,那么可以用身体的“尺子”来测,比如前臂长(包括手掌、手指)(如图4),利用该方法测得一块花岗岩的长和宽(如图5).

问题解决
任务1
获取数据
通过观察、计算B,C两点之间的水平距离及铅垂距离(高度差).
任务2
分析计算
通过观察、计算石拱桥拱圈的半径.
注:测量、计算时,都以“肘”为单位.
25. 【证明体验】 (1)、如图1,是等腰的外接圆, , 在上取一点 , 连结 , 求证:;(2)、【思考探究】
(1)、如图1,是等腰的外接圆, , 在上取一点 , 连结 , 求证:;(2)、【思考探究】
如图2,在(1)条件下,若点为的中点, , 求的值;(3)、【拓展延伸】
如图3,的半径为5,弦 , 弦 , 延长交的延长线于点 , 且 , 求的值.
-