备考2024年浙江中考数学一轮复习专题21.1四边形基础夯实

试卷更新日期：2024-03-02 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 过某个多边形的一个顶点的所有对角线，将这个多边形分成7个三角形，则这个多边形是（　　）

A、六边形 B、七边形 C、八边形 D、九边形

查看试题解析
2. 下列几种形状的瓷砖中，只用一种不能够铺满地面的是（　　）

A、正六边形 B、正五边形 C、正方形 D、正三角形

查看试题解析
3. 下列说法中的错误的是（　　）

A、一组邻边相等的矩形是正方形 B、一组邻边相等的平行四边形是菱形 C、一组对边相等且有一个角是直角的四边形是矩形 D、一组对边平行且相等的四边形是平行四边形

查看试题解析
4. 在菱形ABCD中，∠B＝60°，用六条线段（虚线表示）把菱形分割成四部分，如图所示，其中PM∥EF∥BC ， PF∥MN∥CD ， FG∥MH∥AC ，且点P在对角线AC上，若求该六条割线长（虚线部分）的和，只需知道（）

A、六边形PMHCGF的周长 B、梯形EFGB的周长 C、梯形MNDH的周长 D、菱形ABCD的周长

查看试题解析
5. 如图，在正方形 $A B C D$ 中， $E$ 为线段 $C D$ 上一点且 $C E = \frac{1}{4} C D$ ，连结 $A C$ ， $B E$ 交于点 $F$ ，分别作 $A C$ ， $B E$ 的中点M ， N ，连结 $M N$ ，若 $A B = 4$ ，则 $M N$ 为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\sqrt{2}$

查看试题解析
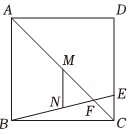6. 如图是一张长方形纸片ABCD，点M是对角线AC的中点，点E在BC边上，把△DCE沿直线DE折叠，使点C落在对角线AC上的点F处，连接DF、EF，若MF=CD，则∠DAF的度数为（）

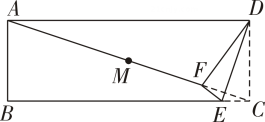A、15° B、16° C、18° D、20°

查看试题解析
7. 如图一标志性建筑的底面呈正方形，底面采用4块完全相同的长方形地砖和一块正方形地砖拼成，则以下说法正确的是 $($ $)$

A、由长方形地砖的周长可求外面大正方形的面积 B、由长方形地砖的面积可求外面大正方形的面积 C、由里面小正方形地砖的周长可求长方形的面积 D、由里面小正方形地砖的面积可求大正方形的面积

查看试题解析
8. 如图，在菱形 $A B C D$ 中， $∠ B = 60 °$ ，点 $O$ 为对称中心，点 $E$ 从点 $A$ 出发沿 $A B$ 向点 $B$ 移动，移动到点 $B$ 停止，连接 $E O$ 并延长交边 $C D$ 于点 $F$ ，连接 $E C$ ， $A F$ ．则四边形 $A E C F$ 形状的变化依次为（）

A、平行四边形→矩形→正方形→菱形 B、平行四边形→矩形→平行四边形→菱形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→平行四边形→菱形

查看试题解析
9. 如图，一块长方形场地ABCD的长AB与宽AD的比为 $2 ： 1 ， D E ⊥ A C$ 于点 $E$ ， $B F ⊥ A C$ 于点 $F$ ，连接BE，DF，则四边形DEBF与长方形ABCD的面积比为（）

A、 $\frac{3}{10}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析
10. 如图，正方形ABCD中，AC ， E为线段BO上一动点（不包括O ， B两点），DF⊥CE于点F ，过点A作AG⊥DF于点G，交BD于点H ，连结AE ，则下列结论：①∠ADG＝∠DCF；②DG＝EF ， ③存在点E，使得EF＝GF；④四边形AECH是菱形．其中正确的结论有（）

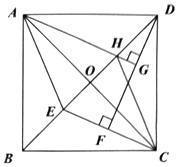A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共18分

11. 若一个正多边形的每个内角为 $135 °$ ，则这个正多边形的边数是．

查看试题解析
12. 如图，矩形ABCD的对角线AC，BD交于点O，AB=6，BC=8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为.

查看试题解析
13. 如图，已知 $△ A B C$ 的面积为 $24$ ，点 $D$ 在线段 $A C$ 上，点 $D$ 在线段 $B C$ 的延长线上，且 $B F = 4 C F$ ，四边形 $D C F E$ 是平行四边形，则图中阴影部分的面积是．

查看试题解析
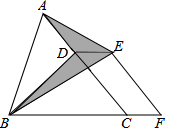14. 如图，在菱形ABCD中， $A B = 6$ ， $∠ A = 60 °$ ，将菱形ABCD沿菱形ABCD某一边平移a长度，得菱形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ ；将菱形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 沿菱形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 某一边平移a长度，得菱形 $A_{2} B_{2} C_{2} D_{2}$ ；将菱形 $A_{2} B_{2} C_{2} D_{2}$ 沿菱形 $A_{2} B_{2} C_{2} D_{2}$ 某一边平移a长度，得菱形 $A_{3} B_{3} C_{3} D_{3}$ ；若四个菱形构成的整个图形为中心对称图形，且四个菱形重叠部分面积为 $8 \sqrt{3}$ ，则 $a =$ ．

查看试题解析
15. 如图 $1$ 是七巧板图案，现将它剪拼成一个“台灯”造型 $($ 如图 $2)$ ，过该造型的上下左侧五点作矩形 $A B C D$ ，使得 $\frac{A B}{B C} = \frac{3}{5}$ ，点 $N$ 为 $P Q$ 的中点，并且在矩形内右上角部分留出正方形 $E F G H$ 作为印章区域 $(E H / / A D ， H G / / C D)$ ，形成一幅装饰画，则矩形 $A B C D$ 的周长为 $c m .$ 若点 $M$ ， $N$ ， $E$ 在同一直线上，且点 $H$ 到 $A D$ 的距离与到 $C D$ 的距离相等，则印章区域的边长为 $c m$ ．

查看试题解析
16. 郑在一次拼图游戏中，发现了一个很神奇的现象：
⑴他先用图形①②③④拼出矩形ABCD.
⑵接着拿出图形⑤ .
⑶通过平移的方法，用①②③④⑤拼出了矩形ABMN.已知AE：EO = 2：3，图形④的面积为15，则增加的图形⑤的面积为：，当CO= $3 \frac{1}{2}$ ， EH=4时，tan∠BAO=.

查看试题解析

三、解答题（共7题，共52分）

17. 在学习多边形的相关知识时，小张同学和小王同学对老师布置“探究多边形的对角线条数”的作业很感兴趣，小张同学探究得到了 $n$ 边形的对角线条数的公式，并通过上网查证自己探究的结论是正确的．下图是两位同学进行交流的情景．小王同学把哪个多边形对角线的条数数错了？请你通过计算或者画图来说明．

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中，延长 $B C$ 至点F，延长 $C B$ 至点E，且 $B E = C F ， D E = A F$ ．求证：平行四边形 $A B C D$ 是矩形．

查看试题解析
19. 如图，在▱ABCD中，O为线段AD的中点，延长BO交CD的延长线于点E ，连接AE ， BD ， ∠BDC＝90°．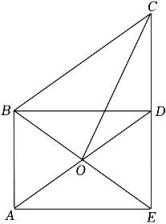

(1)、求证：四边形ABDE是矩形；

(2)、连接OC ，若AB＝2， $B D = 2 \sqrt{2}$ ，求OC的长．

查看试题解析
20. 如图1，四边形ABCD为正方形，点A在y轴上，点B在x轴上，且OA＝2OB，反比例函数 $y = \frac{27}{x}$ 在第一象限的图象经过正方形的顶点C．

(1)、求点C的坐标；

(2)、如图2，将正方形ABCD沿x轴向右平移得到正方形 A'B'CD'，点 A'恰好落在反比例函数的图象上，求此时点 D'的坐标；

(3)、在（2）的条件下，点P为y轴上一动点，平面内是否存在点Q，使以点O、A'、P、Q为顶点的四边形为菱形，若存在，请直接写出点Q的坐标，若不存在，请说明理由．

查看试题解析
21. 如图1，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC=PA，PD=PB，∠APC=∠BPD，连接CD，点E、F、G、H分别是AC、AB、BD、CD的中点，顺次连接E、F、G、H．

(1)、猜想四边形EFGH的形状是.（直接回答，不必说明理由）

(2)、当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，（1）中的结论还成立吗？说明理由；

(3)、如果（2）中，∠APC=∠BPD=90°，其他条件不变，先在图3中补全图形，再判断四边形EFGH的形状，并说明理由．

查看试题解析
22. 如图1，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点E，F分别在 $A D$ ， $B C$ 上，将矩形 $A B C D$ 沿直线 $E F$ 折叠，使点B落在 $C D$ 边上的 $B^{'}$ 处，点A落在 $A^{'}$ 处，连接 $B B^{'}$ ．

(1)、如图2，若点 $B^{'}$ 与点D重合，连接 $E B$ ．

①请你判断四边形 $E B F B$ 的形状，并证明；
②求 $E F$ 的长；

(2)、如图3，P为 $A^{'} B^{'}$ 中点，连接 $B P$ ．

①当 $C B^{'} = 2$ 时，求 $B P$ 的长；

②直接写出 $B P$ 的取值范围．

查看试题解析
23. 如图1，在矩形ABCD中，AB=6，BC=6 $\sqrt{3}$ .对角线AC， BD相交于点O，点E， F分别在对角线AC，BD.上，CE=2AE，连结EF.

(1)、求线段OE的长和∠AOB的度数.

(2)、当点F在点B处时，以EF为边在右下方作等边△EFG，连结OG.在点F运动过程中，点G也随之运动.如图2，过点F作AB的平行线交AC于点H.若设线段BF长为x，线段OG长为y，求y关于x的函数关系式，并写出相应x的取值范围.

(3)、若点F在直线BD上运动，以EF为边作等边△EFG.当点G恰好落在矩形ABCD的边上时，求FG的长.

查看试题解析

四、实践探究题（共2题，共20分）

24. 【发现与证明】
如图，在四边形ABCD中，E、F、G、H是各边中点，对角线AC、BD相交于点O，I、J是AC、BD的中点，连接EF、EH、HG、GF、EI、GI、EJ、FJ、IJ、GJ、IH.
结论1：四边形EFGH是平行四边形；
结论2：四边形EJGI是平行四边形；
结论3： $S_{四边形 E F G H} = \frac{1}{2} S_{四边形 A B C D}$ ；
……

(1)、请选择其中一个结论，加以证明（只需证明一个结论）.

(2)、【探究与应用】（★温馨提示：以下问题可以直接使用上述结论）
①如图1，在四边形ABCD中，F、H分别为边AB，DC的中点，连结HF.已知 $A D = 6$ ， $B C = 4$ ，线段HF的取值范围是 ▲ .
②如图2，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，连接EG，FH交于点O， $E G = 8$ cm， $F H = 6$ cm， $∠ E O F = 60 °$ ，求 $S_{四边形 A B C D}$ .

查看试题解析
25. 菱形 $A B C D$ 的边长为 $30$ ， $∠ A D C = 120 °$ ，点 $O$ 是对角线 $A C$ 中点， $M$ 是线段 $O C$ 上任一点，连接 $D M$ ，作 $∠ D M N = 120 °$ ，边 $M N$ 与直线 $A B$ 相交于点 $N$ ．

小南和小浦观察以上问题时，猜想 $D M = M N$ ，老师引导他们用“从特殊到一般”的思想方法去尝试研究．

(1)、【特例发现】
小南发现：当点 $M$ 与点重合时， $D M$ 与 $M N$ 的长度相等，为；

(2)、【探究证明】
小浦认为当 $N$ 在线段 $A B$ 上时，均有“ $D M = M N$ ”，请帮助完成证明．

(3)、【拓展运用】
①连结 $D N$ 交 $A C$ 于点 $E$ ，求证： $∠ A D E + ∠ M D C$ 为定值．
②当 $M N^{2} + D E^{2} = A E^{2}$ 时， $S_{△ A D E} =$ ▲ ．

查看试题解析

备考2024年浙江中考数学一轮复习专题21.1四边形 基础夯实

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分

三、解答题（共7题，共52分）

四、实践探究题（共2题，共20分）

备考2024年浙江中考数学一轮复习专题21.1四边形基础夯实