备考2024年浙江中考数学一轮复习专题21.2四边形 真题模拟集训
试卷更新日期:2024-03-02 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 下列命题正确的是( )A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形2. 已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )A、6 B、7 C、8 D、93. 用四个全等的直角三角形无空隙、无重叠地拼成一个菱形,该菱形的边长的平方等于两条对角线的积,则这四个直角三角形的最小内角是( )A、60° B、45° C、30° D、15°4. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
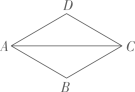 A、 B、1 C、 D、5. 如图,已知∠AOB , 以点O为圆心,适当长为半径作圆弧,与角的两边分别交于C , D两点,分别以点C , D为圆心,大于长为半径作圆弧,两条圆弧交于∠AOB内一点P , 连结OP , 过点P作直线PE∥OA , 交OB于点E , 过点P作直线PF∥OB , 交OA于点F . 若∠AOB=60°,OP=6cm , 则四边形PFOE的面积是( )
A、 B、1 C、 D、5. 如图,已知∠AOB , 以点O为圆心,适当长为半径作圆弧,与角的两边分别交于C , D两点,分别以点C , D为圆心,大于长为半径作圆弧,两条圆弧交于∠AOB内一点P , 连结OP , 过点P作直线PE∥OA , 交OB于点E , 过点P作直线PF∥OB , 交OA于点F . 若∠AOB=60°,OP=6cm , 则四边形PFOE的面积是( )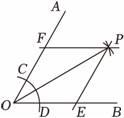 A、 cm2 B、 cm2 C、 cm2 D、 cm26. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( )
A、 cm2 B、 cm2 C、 cm2 D、 cm26. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( ) A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形7. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:
A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形7. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:①存在无数个平行四边形 ;
②存在无数个矩形 ;
③存在无数个菱形 ;
④存在无数个正方形 .其中正确的个数是( )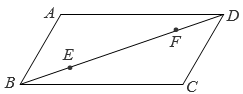 A、1 B、2 C、3 D、48. 如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的是( )
A、1 B、2 C、3 D、48. 如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的是( ) A、①③④ B、②④⑤ C、①③④⑤ D、①③⑤9. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O,BD与HC相交于点P.若 ,下列结论:① ,② ,③ ,④ .正确的是( )
A、①③④ B、②④⑤ C、①③④⑤ D、①③⑤9. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O,BD与HC相交于点P.若 ,下列结论:① ,② ,③ ,④ .正确的是( ) A、②③④ B、①③④ C、①②④ D、①②③10. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:
A、②③④ B、①③④ C、①②④ D、①②③10. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;
第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.
则DH的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .
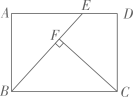 12. 如图,正六边形ABCDEF的边长为2cm,点P是线段BF上一点,则阴影部分的面积为cm2
12. 如图,正六边形ABCDEF的边长为2cm,点P是线段BF上一点,则阴影部分的面积为cm2 13. 如图,矩形ABCD中,AB=1,BC=2,AE为∠BAD的平分线,F为AE上一动点,点M为DF的中点,连接BM,则BM的最小值是.
13. 如图,矩形ABCD中,AB=1,BC=2,AE为∠BAD的平分线,F为AE上一动点,点M为DF的中点,连接BM,则BM的最小值是. 14. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .
14. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .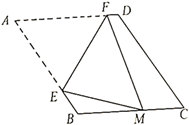 15. 如图,在矩形ABCD中,点E是AD的中点,连接BE , 将△ABE沿着BE翻折得到△FBE , EF交BC于点H , 延长BF , DC相交于点G , 若DG=8,BC=12,则AB= , EH= .
15. 如图,在矩形ABCD中,点E是AD的中点,连接BE , 将△ABE沿着BE翻折得到△FBE , EF交BC于点H , 延长BF , DC相交于点G , 若DG=8,BC=12,则AB= , EH= . 16. 如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD , 相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF , ③和④分别是Rt△CDG和Rt△DAH , ⑤是正方形EFGH , 直角顶点E , F , G , H分别在边BF , CG , DH , AE上.
16. 如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD , 相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF , ③和④分别是Rt△CDG和Rt△DAH , ⑤是正方形EFGH , 直角顶点E , F , G , H分别在边BF , CG , DH , AE上. (1)、若EF=3cm , AE+FC=11cm , 则BE的长是 cm .(2)、若 , 则tan∠DAH的值是 .
(1)、若EF=3cm , AE+FC=11cm , 则BE的长是 cm .(2)、若 , 则tan∠DAH的值是 .三、作图题(共6分)
-
17. 分别在图①、图②中按要求作图(保留作图痕迹,不写作法).
 (1)、如图①,在的方格纸中,点都在格点上,在图①中找一个格点D,使以点为顶点的四边形是平行四边形;(2)、如图②,已知四边形是平行四边形,为对角线,点P为上任意一点,请仅用无刻度的直尺在上找出另一点Q,使 .
(1)、如图①,在的方格纸中,点都在格点上,在图①中找一个格点D,使以点为顶点的四边形是平行四边形;(2)、如图②,已知四边形是平行四边形,为对角线,点P为上任意一点,请仅用无刻度的直尺在上找出另一点Q,使 .四、解答题(共5题,共38分)
-
18. 小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.

小惠:
证明:∵AC⊥BD,OB=OD,
∴AC垂直平分BD.
∴AB=AD,CB=CD,
∴四边形ABCD是菱形.
小洁:
这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
19. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .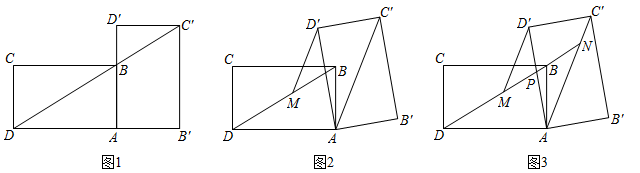
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
20. 正方形ABCD的边长为1,连接BD , 过点C作BD的平行线CE , BE与CD相交于点F , 过点D作DH⊥BE . (1)、求△BDE的面积;(2)、当∠CBE=15°时,求BE的长;(3)、若△EFC的面积记为S1 , △DFH的面积记为S2 , △DBF的面积记为S3 , △BFC的面积记为S4 , , 请用k的代数式表示的值.21. 如图1,点为矩形ABCD的对称中心, , 点为AD边上一点 , 连结EO并延长,交BC于点.四边形ABFE与关于EF所在直线成轴对称,线段交AD边于点。
(1)、求△BDE的面积;(2)、当∠CBE=15°时,求BE的长;(3)、若△EFC的面积记为S1 , △DFH的面积记为S2 , △DBF的面积记为S3 , △BFC的面积记为S4 , , 请用k的代数式表示的值.21. 如图1,点为矩形ABCD的对称中心, , 点为AD边上一点 , 连结EO并延长,交BC于点.四边形ABFE与关于EF所在直线成轴对称,线段交AD边于点。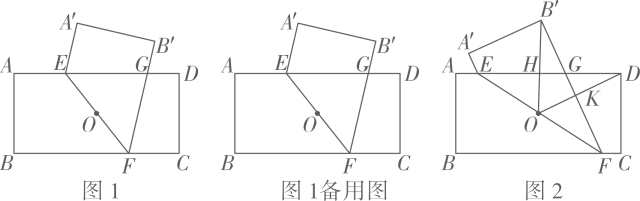 (1)、求证:.(2)、当时,求AE的长.(3)、令AE=a,DG=b.
(1)、求证:.(2)、当时,求AE的长.(3)、令AE=a,DG=b.①求证:(4-a)(4-b)=4.
②如图2,连结 , 分别交于点H,K.记四边形OKGH的面积为 , 的面积为.当时,求的值.
22. 如图,在矩形ABCD中,AD=2 ,AB=4 ,DM⊥AC于点M , 在对角线AC上取一点N , 使得2CN=3AM , 连接DN并延长交BC于点E , F是AB上一点,连接EF , MF . 当点P从点E匀速运动到点F时,点Q恰好从点M匀速运动到点N . (1)、求AM , CE的长.(2)、若EF∥AC , 记EP=x , AQ=y .
(1)、求AM , CE的长.(2)、若EF∥AC , 记EP=x , AQ=y .①求y关于x的函数表达式.
②连接PQ , 当直线PQ平行于四边形DEFM的一边时,求所有满足条件的x的值.
(3)、在运动过程中,当直线PQ同时经过点B和D时,记点Q的运动速度为v1 , 记点P的运动速度为v2 , 求 的值.五、实践探究题(共3题,共28分)
-
23.
 (1)、【特例感知】
(1)、【特例感知】如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD , 过点D作DM⊥PD , 交BC的延长线于点M . 求证:△DAP≌△DCM .
(2)、【变式求异】如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB , 交AC于点Q , 点P在边AB的延长线上,连结PQ , 过点Q作QM⊥PQ , 交射线BC于点M . 已知BC=8,AC=10,AD=2DB , 求的值.
(3)、【拓展应用】如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A , C重合),连结PQ , 以Q为顶点作∠PQM=∠PBC , ∠PQM的边QM交射线BC于点M . 若AC=mAB , CQ=nAC(m , n是常数),求的值(用含m , n的代数式表示).
24. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD. (1)、[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.(2)、[探究2]如图2,连结AC′,过点D′作 交BD于点M,线段D′M与DM相等吗?请说明理由.(3)、[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.25. 如图,
(1)、[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.(2)、[探究2]如图2,连结AC′,过点D′作 交BD于点M,线段D′M与DM相等吗?请说明理由.(3)、[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.25. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).
-